Code
options(digits = 3)
if (!require("pacman")) install.packages("pacman")
pacman::p_load(tidyverse, magrittr, ggpubr, here,
car, modelsummary, datarium, dae, ggdist) - 2
- 必要なパッケージを読み込み
2024/07/26
2024/07/31
調査者が何らかの操作をして行う調査・研究
参加者をランダムに2つ(以上)のグループに割り振って,片方には新しい薬を,片方には薬ではないもの(プラセボ)を投与して,新薬の効果を検証する
同じ場所に並べた複数の植木のうち,ランダムに選んだいくつかには肥料を与え,残りには与えないことで,肥料の効果を検証する
アクセスしてくる人のうち一定割合に別のデザインの画面を表示し,クリックする先やクリック率等を比較する。(どちらのデザインの方が良いか?)
実験的手法は,調査者が何らかの介入をして,その介入効果を見るようなもの。そのような特徴から
元々理系では実験的手法が中心だったけれど,上記の特徴から社会科学領域でも実験的研究が重視されてきている。2019年のノーベル経済学賞をとったBanerjee, Duflo, Kremerも「世界の貧困を改善するための実験的アプローチに関する功績」
一方で,
xがyの原因となる
「国民健康・栄養調査」による年齢別の身長・体重データ
Call:
lm(formula = Height_m ~ Weight_m, data = height_weight)
Residuals:
Min 1Q Median 3Q Max
-19.02 -6.79 1.33 6.58 12.11
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 84.7973 2.4348 34.8 <2e-16 ***
Weight_m 1.3391 0.0464 28.9 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.61 on 60 degrees of freedom
Multiple R-squared: 0.933, Adjusted R-squared: 0.932
F-statistic: 834 on 1 and 60 DF, p-value: <2e-16身長と体重は有意に正の関係がある。
でも,これは明らかに因果関係ではない。
おそらく単なる相関関係
偶然相関があるように見える
人口あたりのチーズの消費量とベッドシーツに絡まって死ぬ人の数
アメリカの科学・宇宙・テクノロジーに対する支出と首吊り,絞殺,窒息による自殺者数
つまり…
単に相関を計算したり,回帰分析をしただけではx → yという因果関係はわからない。
因果関係を推論することは結構難しい。
仮に薬の効果を知りたいとしたら,薬を投与した人と投与しない人1人ずつのその効果(例えば血液検査の結果数値など)を比べる?
適切な比較はできない
本来的には薬の効果(薬と症状改善の因果関係)は「同じ人が投与した場合と投与していない場合」を比較しないといけない。
でも,現実に観察されるのはどっちか。薬ありもしくは薬なしどっちかのデータしか取れない。
パラレルワールド・タイムマシンがない限り実現できない。反実仮想が必要。
因果推論の根本問題とか言われる
たくさんの参加者を集めて,その人たちにランダムに処置(投与するかしないか)を割り振る
ランダムに割り振った集団間の比較をすることで薬の「平均的な」効果を推定することができる
個人レベルで見ると因果関係はそもそも検証が不可能
集団レベルでランダムに処置を割り振ることで,平均的な効果の推定を通した因果関係が可能
このことを使って
| Level | 内容 |
|---|---|
| 1a | ランダム化比較試験のメタアナリシス |
| 1b | 少なくとも一つのランダム化比較試験 (RCT) |
| 2a | ランダム割付を伴わない同時コントロールを伴うコホート研究(前向き研究、prospective study, concurrent cohort study) |
| 2b | ランダム割付を伴わない過去のコントロールを伴うコホート研究 (historical cohort study, retrospective cohort study) |
| 3 | 症例対照研究(ケースコントロール、後ろ向き研究) |
| 4 | 処置前後の比較の前後比較、対照群を伴わない研究 |
| 5 | 症例報告、ケースシリーズ |
| 6 | 専門家個人の意見(専門家委員会報告を含む) |
Rにサンプルデータとして入っているheadacheデータを使用
ある製薬会社が片頭痛患者を対象に3種類の治療法を試験した。実験には72人の参加者が登録された。その目的は、片頭痛エピソードに関連する痛みのスコアを下げる新しいクラスの治療法の可能性を調べることである。
参加者は男性36名、女性36名である。男性と女性はさらに(等しく)片頭痛のリスクが低いか高いかに細分化された。
以下の変数を含む:
gender性別: 「男性」と「女性」;
riskリスク: 低 “と”高”
treatment治療の種類:3つのカテゴリーがある: X”、“Y”、“Z”の3つのカテゴリーがある。
分析例を簡単にするため,treatment Yを落とした。なので,Xを治療なし,Zを薬による治療と解釈して話を進める
記述統計を見ると,gender(男女)とrisk(高い低い)は各条件に均等に配分されている
| X (N=24) | Z (N=24) | ||||||
|---|---|---|---|---|---|---|---|
| Mean | Std. Dev. | Mean | Std. Dev. | Diff. in Means | p | ||
| pain_score | 80.5 | 8.6 | 76.2 | 5.9 | -4.2 | 0.054 | |
| N | Pct. | N | Pct. | ||||
| gender | male | 12 | 50.0 | 12 | 50.0 | ||
| female | 12 | 50.0 | 12 | 50.0 | |||
| risk | high | 12 | 50.0 | 12 | 50.0 | ||
| low | 12 | 50.0 | 12 | 50.0 | |||
主な分析は分散分析(ANOVA)。Anova(lm(結果 ~ 要因, data = データ名))コマンドで実行可能
(僕は二重括弧が嫌いなので以下のように分けます)
仮説検定での帰無仮説は治療の効果はない。治療の違いの効果は10%水準で有意(\(F_{1,46}\) =3.946, p = 0.053 ; 水準を10%としたら,関係ないと言う帰無仮説は棄却される)
ANOVAの原理はダミー変数を使った回帰分析と一緒。なので以下のような単回帰分析をしても同じ
Call:
lm(formula = pain_score ~ treatment, data = headache)
Residuals:
Min 1Q Median 3Q Max
-12.09 -5.62 -1.17 4.40 19.55
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 80.45 1.50 53.62 <2e-16 ***
treatmentZ -4.22 2.12 -1.99 0.053 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.35 on 46 degrees of freedom
Multiple R-squared: 0.079, Adjusted R-squared: 0.059
F-statistic: 3.95 on 1 and 46 DF, p-value: 0.053更に,性別やそもそもの頭痛リスクを踏まえた分析をしてみる
また,ggline()コマンドを使うと,効果を図に表せる
男女で効き目が違うか
男性の方が効果が大きい。ただし交互作用が有意とまではいかない(\(F_{1,44}\) =2.439, p = 0.126 )
treatment, gender, riskはそれぞれ頭痛の度合いと有意に関係
treatmentとriskとgenderの3要因に交互作用
interaction.ABC.plot (daeパッケージ)を使うと比較的簡単にかける
回帰分析の結果を並べるとこんな感じ
list(
m1 <- lm(pain_score ~ treatment ,
data = headache),
m2 <- lm(pain_score ~ treatment + gender,
data = headache),
m3 <- lm(pain_score ~ treatment * gender,
data = headache),
m4 <- lm(pain_score ~ treatment + risk,
data = headache),
m5 <- lm(pain_score ~ treatment * risk,
data = headache),
m6 <- lm(pain_score ~ treatment + gender + risk,
data = headache),
m7 <- lm(pain_score ~ treatment * gender * risk,
data = headache)
) |>
msummary(models = _,
stars = TRUE,
gof_omit = "Log.Lik.|AIC|BIC|RMSE|F",
statistic = NULL)| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 | |||||||
| (Intercept) | 80.453*** | 82.839*** | 84.395*** | 85.188*** | 85.802*** | 87.574*** | 92.739*** |
| treatmentZ | -4.215+ | -4.215* | -7.327* | -4.215* | -5.444* | -4.215** | -13.058*** |
| genderfemale | -4.773* | -7.885** | -4.773** | -13.874*** | |||
| treatmentZ × genderfemale | 6.224 | 15.228*** | |||||
| risklow | -9.469*** | -10.698*** | -9.469*** | -16.687*** | |||
| treatmentZ × risklow | 2.458 | 11.462** | |||||
| genderfemale × risklow | 11.978** | ||||||
| treatmentZ × genderfemale × risklow | -18.009*** | ||||||
| Num.Obs. | 48 | 48 | 48 | 48 | 48 | 48 | 48 |
| R2 | 0.079 | 0.180 | 0.223 | 0.478 | 0.484 | 0.579 | 0.729 |
| R2 Adj. | 0.059 | 0.144 | 0.170 | 0.454 | 0.449 | 0.550 | 0.681 |
ハンバーガー統計学を参考に作成
| 統制群 | 新フォーマット群 | |
| 会計知識高 | 7, 8, 6, 8, 10, 7, 8, 8, 9, 7 | 8, 9, 10, 10, 8, 8, 9, 7, 10, 8 |
| 会計知識低 | 4, 6, 5, 4, 3, 7, 5, 6, 4, 5 | 8, 7, 8, 6, 9, 7, 8, 8, 10, 8 |
(1) この検定での帰無仮説を言いなさい。
(2) この検定での対立仮説を言いなさい。
(3) 4つの条件におけるそれぞれの平均と標準偏差を計算しなさい(コードと結果)。
(4) 分散分析を行いなさい(コード)。
(5) 有意水準を1%としたとき、この分散分析表から言えることを書きなさい。
(6) 以上の検定の結果を、わかりやすいことばで説明しなさい。
次ページにデータ作成用コマンドがあります。
データ作成
score <- c(7, 8, 6, 8, 10, 7, 8, 8, 9, 7,
8, 9, 10, 10, 8, 8, 9, 7, 10, 8,
4, 6, 5, 4, 3, 7, 5, 6, 4, 5,
8, 7, 8, 6, 9, 7, 8, 8, 10, 8)
knowledge <- c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
format <-c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1)
kadai <- tibble(score, knowledge, format) %>%
mutate(knowledge = factor(knowledge,
levels = c(1, 0),
labels = c("high", "low")),
format = factor(format,
levels = c(1, 0),
labels = c("new", "normal")))---
title: "15 実験的手法と効果検証"
date: 2024/07/26
format:
html: default
revealjs:
output-file: 15_experiment_slide.html
echo: true
code-fold: show
---
## 準備
### パッケージの読み込み
```{r}
#| message: false
#| code-fold: show
options(digits = 3) #<2>
if (!require("pacman")) install.packages("pacman") #<3>
pacman::p_load(tidyverse, magrittr, ggpubr, here,
car, modelsummary, datarium, dae, ggdist)
```
1. 少数第3位まで表示
# 実験的手法とは? {data-stack-name="はじめに"}
------------------------------------------------------------------------
調査者が何らかの操作をして行う調査・研究
.svg){fig-align="center"}
## 例1:治験
参加者をランダムに2つ(以上)のグループに割り振って,片方には新しい薬を,片方には薬ではないもの(プラセボ)を投与して,新薬の効果を検証する

## 例2:肥料の実験
同じ場所に並べた複数の植木のうち,ランダムに選んだいくつかには肥料を与え,残りには与えないことで,肥料の効果を検証する

## 例3:ABテスト
アクセスしてくる人のうち一定割合に別のデザインの画面を表示し,クリックする先やクリック率等を比較する。(どちらのデザインの方が良いか?)
::: {layout="[1,1,1]"}



:::
<div>
::: {style="text-size: smaller;"}
出所:<https://unique1.co.jp/column/ads/4324/>
:::
</div>
## 例4:従業員の業績評価方法
- 企業の人事制度の違いが効果をもたらすのか明らかにするため,ランダムに選択された部署のみ業績評価の方法を変えてみる。評価の方法を変えなかった部署と行動の変化を比較する
- 企業トップのメッセージが現場の従業員の行動に与える影響を見るため,ランダムに選ばれた店舗だけにトップのメッセージ動画を定期的に配信する。メッセージを受け取った店舗と受け取らなかった店舗の行動の違いを比較する [@cronin2021]
# 実験的手法の特徴と経営への応用 {data-stack-name="特徴と応用"}
## 実験的手法の特徴
実験的手法は,調査者が何らかの介入をして,その介入効果を見るようなもの。そのような特徴から
- 因果関係を検証できる
- 実験で検証したい要因以外が調整されているので,堅い証拠が得られる(内的妥当性が高い)
::: {.callout-note appearance="simple" icon="false"}
元々理系では実験的手法が中心だったけれど,上記の特徴から社会科学領域でも実験的研究が重視されてきている。2019年のノーベル経済学賞をとったBanerjee, Duflo, Kremerも「世界の貧困を改善するための実験的アプローチに関する功績」
:::
一方で,
- 実験環境以外でも同じような結果が得られるかはわからない(外的妥当性が低い)
- 実験で検証できる要因(≒調査者が操作できる要因)しか実験できない
- 「職場における仲の良さが,仕事に対するモチベーションに与える影響」みたいなのは研究しづらい。
- 「株式市場の値動き」みたいなのも研究しづらい
## 実験研究と因果推論
- 実験研究と関連して,統計的手法を用いた因果関係の推論(統計的因果推論)が注目されつつある
- 2021年のノーベル経済学賞をとったCard, Angrist, Imbensの受賞理由は「因果関係の分析への方法論的貢献」
- 回帰分析は,yを結果,xを原因とみなした因果関係を検証しているように見える(し,多くの場合因果関係を暗に想定している)が,実際に算出しているのは相関関係
- 逆因果の可能性も否定できない。
- 実験的な調査方法と組み合わせることで,回帰分析の結果は因果関係と見なせる
- 他の調査方法で因果関係を証明するためには,統計的に行動な技術が必要
- 過激派は実験以外では因果関係は証明不可能と主張
# 因果関係 {data-stack-name="因果関係"}
## 因果関係って?
xがyの原因となる
- ある薬Aが,病気Zを直す
{fig-align="center" width="791"}
- ある広告Bが,売上高Sを高くする
{fig-align="center" width="1016"}
## 相関≠因果関係
### 単なる相関
「国民健康・栄養調査」による年齢別の身長・体重データ
::::: columns
::: {.column width="35%"}
```{r}
#| code-fold: true
#| fig-width: 6
#| fig-height: 6
height_weight <- here("data",
"12_height_weight.csv") |> read_csv()
height_weight |>
ggplot(aes(x = Weight_m, y = Height_m)) +
geom_point()
```
:::
::: {.column width="65%"}
```{r}
#| code-fold: true
lm(Height_m ~ Weight_m,
data = height_weight) |>
summary()
```
:::
:::::
------------------------------------------------------------------------
身長と体重は有意に正の関係がある。
- 体重が1kg重いと身長が1.34cm高い。
でも,これは明らかに因果関係ではない。
- 体重が重くなるから身長が伸びる**わけではない**
- 身長を伸ばしたかったら体重を重くすればいい**わけではない**
おそらく単なる相関関係
{fig-align="center" width="660"}
------------------------------------------------------------------------
### 単なる偶然(擬似相関)
偶然相関があるように見える
{fig-align="center"}
人口あたりのチーズの消費量とベッドシーツに絡まって死ぬ人の数
------------------------------------------------------------------------
{fig-align="center"}
アメリカの科学・宇宙・テクノロジーに対する支出と首吊り,絞殺,窒息による自殺者数
------------------------------------------------------------------------
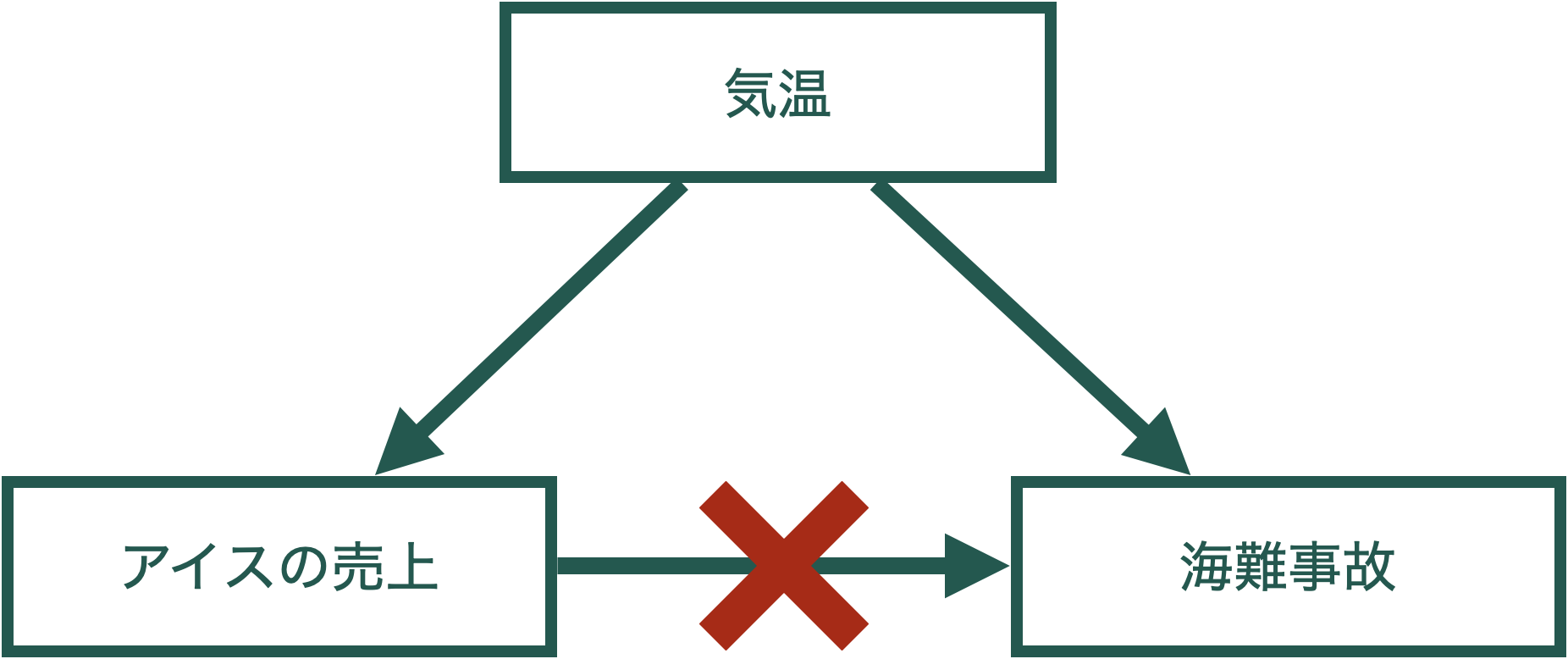
### 共通の要因がある(交絡)
{fig-align="center"}
つまり...
単に相関を計算したり,回帰分析をしただけではx → yという因果関係はわからない。
# 因果推論 {data-stack-name="因果推論"}
因果関係を推論することは結構難しい。
## 個人レベルで考えると...
仮に薬の効果を知りたいとしたら,薬を投与した人と投与しない人1人ずつのその効果(例えば血液検査の結果数値など)を比べる?
::: nostretch
{.nonstretch fig-align="center" width="663"}
:::
適切な比較はできない
- そもそもの病状が違うかもしれない
- 体格や薬で治そうとしている病気以外の持病の状況が違うかもしれない
------------------------------------------------------------------------
本来的には薬の効果(薬と症状改善の因果関係)は「[**同じ人が**]{.green}投与した場合と投与していない場合」を比較しないといけない。
::: nostretch
{fig-align="center" width="794"}
:::
でも,現実に観察されるのはどっちか。薬ありもしくは薬なしどっちかのデータしか取れない。
- 投与した人の,仮に投与しなかった場合の結果は不明
- 投与しなかった人の仮に投与した場合の結果は不明
パラレルワールド・タイムマシンがない限り実現できない。反実仮想が必要。
[**因果推論の根本問題**]{.green}とか言われる
## 集団レベルで見ると
たくさんの参加者を集めて,その人たちにランダムに処置(投与するかしないか)を割り振る
- これによって個人個人の差は平均的に同じになる
- 症状が重い人軽い人,その他持病がある人ない人,性別などは確率的に均一になることが期待される
ランダムに割り振った集団間の比較をすることで薬の「**平均的な**」効果を推定することができる
- ATE (Average Treatment Effect)
{fig-align="center" width="1183"}
## つまり...
- 個人レベルで見ると因果関係はそもそも検証が不可能
- 集団レベルでランダムに処置を割り振ることで,平均的な効果の推定を通した因果関係が可能
このことを使って
- たくさんのデータを使って統計的な分析をすることにより,因果関係を推定する事が可能かもしれない
## 経営での応用可能性
- 経営学研究や経営の実務においても,何かしらの効果を検証したい場合には,実験的手法を思い浮かべると良さそう
- 実験が可能ならば,実験を
- 実験が不可能なら,実験に近い設定で検証するにはどんな工夫をすればよいか?
------------------------------------------------------------------------
::: callout-note
### 参考: エビデンスレベル
- 根拠に基づく医療(Evidence Based Medicine: EBM)という考え方の中の言葉
- 各研究方法から得られる証拠(エビデンス)をその信頼度で分類している
- 根拠に基づく政策立案(EBPM)や,根拠に基づく経営(EBMgt) [@rousseau2006] として,経営学を含む他分野でも紹介されつつある
| Level | 内容 |
|:----------------------:|:-----------------------------------------------|
| 1a | [ランダム化比較試験](https://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%83%80%E3%83%A0%E5%8C%96%E6%AF%94%E8%BC%83%E8%A9%A6%E9%A8%93 "ランダム化比較試験")の[メタアナリシス](https://ja.wikipedia.org/wiki/%E3%83%A1%E3%82%BF%E3%82%A2%E3%83%8A%E3%83%AA%E3%82%B7%E3%82%B9 "メタアナリシス") |
| 1b | 少なくとも一つの[ランダム化比較試験](https://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%83%80%E3%83%A0%E5%8C%96%E6%AF%94%E8%BC%83%E8%A9%A6%E9%A8%93 "ランダム化比較試験") (RCT) |
| 2a | ランダム割付を伴わない同時コントロールを伴う[コホート研究](https://ja.wikipedia.org/wiki/%E3%82%B3%E3%83%9B%E3%83%BC%E3%83%88%E7%A0%94%E7%A9%B6 "コホート研究")(前向き研究、prospective study, concurrent cohort study) |
| 2b | ランダム割付を伴わない過去のコントロールを伴うコホート研究 (historical cohort study, retrospective cohort study) |
| 3 | [症例対照研究](https://ja.wikipedia.org/wiki/%E7%97%87%E4%BE%8B%E5%AF%BE%E7%85%A7%E7%A0%94%E7%A9%B6 "症例対照研究")(ケースコントロール、後ろ向き研究) |
| 4 | 処置前後の比較の前後比較、対照群を伴わない研究 |
| 5 | 症例報告、ケースシリーズ |
| 6 | 専門家個人の意見(専門家委員会報告を含む) |
: エビデンスレベル一覧([Wikipedia](https://ja.wikipedia.org/wiki/%E6%A0%B9%E6%8B%A0%E3%81%AB%E5%9F%BA%E3%81%A5%E3%81%8F%E5%8C%BB%E7%99%82)から)
:::
# 実験におけるデータ分析例 {data-stack-name="分析例"}
## データ
Rにサンプルデータとして入っている`headache`データを使用
ある製薬会社が片頭痛患者を対象に3種類の治療法を試験した。実験には72人の参加者が登録された。その目的は、片頭痛エピソードに関連する痛みのスコアを下げる新しいクラスの治療法の可能性を調べることである。
参加者は男性36名、女性36名である。男性と女性はさらに(等しく)片頭痛のリスクが低いか高いかに細分化された。
以下の変数を含む:
`gender`性別: 「男性」と「女性」;
`risk`リスク: 低 "と"高"
`treatment`治療の種類:3つのカテゴリーがある: X"、"Y"、"Z"の3つのカテゴリーがある。
```{r}
data("headache")
headache
```
------------------------------------------------------------------------
```{r}
data("headache")
headache <- headache |>
filter(treatment != "Y") |>
mutate(treatment = as.character(treatment),
treatment = factor(treatment)) #<1>
```
1. treatmentはもともとfactor型の変数。filterでYを落とすだけだと,サンプルサイズ0のYが残ってしまう。
分析例を簡単にするため,treatment Yを落とした。なので,Xを治療なし,Zを薬による治療と解釈して話を進める
\
## 記述統計量
記述統計を見ると,`gender`(男女)と`risk`(高い低い)は各条件に均等に配分されている
- 単純な比較でも有意な差がある
```{r}
datasummary_balance(pain_score + gender + risk ~
treatment,
dinm_statistic = "p.value",
data = headache)
```
------------------------------------------------------------------------
```{r}
ggplot(data = headache,
aes(x = treatment,
y = pain_score)) +
geom_boxplot() +
theme_ggdist()
```
## 分析方法(分散分析)
主な分析は**分散分析(ANOVA)**。`Anova(lm(結果 ~ 要因, data = データ名))`コマンドで実行可能
(僕は二重括弧が嫌いなので以下のように分けます)
::: {style="font-size: smaller;"}
```{r}
a <- lm(pain_score ~ treatment,
data = headache) |>
Anova()
a
```
:::
仮説検定での帰無仮説は**治療の効果はない。**治療の違いの効果は10%水準で有意($F_{1,46}$ =`{r} a['treatment','F value']`, *p* = `{r} a['treatment','Pr(>F)']` ; 水準を10%としたら,関係ないと言う帰無仮説は棄却される)
------------------------------------------------------------------------
**ANOVAの原理はダミー変数を使った回帰分析と一緒**。なので以下のような単回帰分析をしても同じ
::: {style="font-size: smaller;"}
```{r}
lm(pain_score ~ treatment,
data = headache) |>
summary()
```
:::
------------------------------------------------------------------------
更に,性別やそもそもの頭痛リスクを踏まえた分析をしてみる
### リスクを含めた分析
```{r}
a <- lm(pain_score ~ treatment * risk,
data = headache) |>
Anova()
a
```
- **治療の効果は5%水準で有意に** ($F_{1,44}$ =`{r} a['treatment','F value']`, *p* = `{r} a['treatment','Pr(>F)']` )
- **リスクも有意。リスクが高い人は頭痛度合いが強い**($F_{1,44}$ =`{r} a['risk','F value']`, *p* = `{r} a['risk','Pr(>F)']` )
- **効果は似た感じ(交互作用はない)**($F_{1,44}$ =`{r} a['treatment:risk','F value']`, *p* = `{r} a['treatment:risk','Pr(>F)']` )
------------------------------------------------------------------------
また,`ggline()`コマンドを使うと,効果を図に表せる\
```{r}
ggline(data = headache,
x = "treatment",
y = "pain_score",
color = "risk",
add = c("mean")) +
theme_ggdist()
```
------------------------------------------------------------------------
### 性別を含めた分析
男女で効き目が違うか
```{r}
a <- lm(pain_score ~ treatment * gender,
data = headache) |>
Anova()
a
```
**男性の方が効果が大きい。ただし交互作用が有意とまではいかない**($F_{1,44}$ =`{r} a['treatment:gender','F value']`, *p* = `{r} a['treatment:gender','Pr(>F)']` )
------------------------------------------------------------------------
```{r}
ggline(data = headache,
x = "treatment",
y = "pain_score",
color = "gender",
add = c("mean")) +
theme_ggdist()
```
------------------------------------------------------------------------
### 3要因を含んだ分析
```{r}
lm(pain_score ~ treatment + risk + gender,
data = headache) |>
Anova()
```
**treatment, gender, riskはそれぞれ頭痛の度合いと有意に関係**
------------------------------------------------------------------------
```{r}
lm(pain_score ~ treatment * risk * gender,
data = headache) |>
Anova()
```
`treatment`と`risk`と`gender`の3要因に交互作用
- これがどう言う意味かというと...次のページの図から,**「男性で,尚且つリスクが高い人」にとって,治療Zは効果がある**
------------------------------------------------------------------------
```{r}
int <- interaction.ABC.plot(data = headache,
response = pain_score, #<1>
x.factor = treatment,
groups.factor = gender,
trace.factor = risk)
int +
theme_ggdist()
```
1. 3要素の図表は`interaction.ABC.plot` (`dae`パッケージ)を使うと比較的簡単にかける
------------------------------------------------------------------------
回帰分析の結果を並べるとこんな感じ
```{r}
#| code-fold: true
list(
m1 <- lm(pain_score ~ treatment ,
data = headache),
m2 <- lm(pain_score ~ treatment + gender,
data = headache),
m3 <- lm(pain_score ~ treatment * gender,
data = headache),
m4 <- lm(pain_score ~ treatment + risk,
data = headache),
m5 <- lm(pain_score ~ treatment * risk,
data = headache),
m6 <- lm(pain_score ~ treatment + gender + risk,
data = headache),
m7 <- lm(pain_score ~ treatment * gender * risk,
data = headache)
) |>
msummary(models = _,
stars = TRUE,
gof_omit = "Log.Lik.|AIC|BIC|RMSE|F",
statistic = NULL)
```
# まとめ {data-stack-name="まとめ"}
------------------------------------------------------------------------
- 実験研究の特徴と具体的な分散方法について扱いました。
- 実験は,厳密な因果関係の推論ができる反面,社会調査において実験できる機会や状況は限られている
- 実験では主に分散分析が使われるけれど,本質は回帰分析と同じ
# 課題 {data-stack-name="課題"}
[ハンバーガー統計学](https://kogolab.chillout.jp/elearn/hamburger/chap7/sec9.html)を参考に作成
------------------------------------------------------------------------
- ある企業では,店舗の業績測定・フィードバック方法が複雑すぎると考えています。そこで,現在の業績指標フォーマットの情報を厳選し,シンプルなフォーマットを作成しました。
- シンプルになったので,各店舗の店長は情報をより上手く読み取り,店舗管理に利用できると考えられます。
- 一方で,情報量自体は減っているので,必ずしも店舗管理にプラスの影響を与えるとは限らないという意見もあります。
- この効果を調べるために,店舗(店長)をランダムに2グループに分け,ある店舗では従来のフォーマットを,別の店舗では新しいフォーマットを使うようにしてもらいました。
- 店舗業績のうち,特に店長の判断が影響しそうな部分を取り出し,エリアマネージャーたちに店長の意思決定の巧拙を10段階で評価してもらいました。
- 店長の会計知識について事前にテストをしていたため,そのデータを合わせて利用します。
- 中央値で分けて「会計知識高」と「会計知識低」としました。
| | | |
|-------------------|--------------------------|----------------------------|
| | 統制群 | 新フォーマット群 |
| 会計知識高 | 7, 8, 6, 8, 10, 7, 8, 8, 9, 7 | 8, 9, 10, 10, 8, 8, 9, 7, 10, 8 |
| 会計知識低 | 4, 6, 5, 4, 3, 7, 5, 6, 4, 5 | 8, 7, 8, 6, 9, 7, 8, 8, 10, 8 |
(1) この検定での帰無仮説を言いなさい。
(2) この検定での対立仮説を言いなさい。
(3) 4つの条件におけるそれぞれの平均と標準偏差を計算しなさい(コードと結果)。
(4) 分散分析を行いなさい(コード)。
(5) 有意水準を1%としたとき、この分散分析表から言えることを書きなさい。
(6) 以上の検定の結果を、わかりやすいことばで説明しなさい。
::: red
次ページにデータ作成用コマンドがあります。
:::
------------------------------------------------------------------------
データ作成
```{r}
score <- c(7, 8, 6, 8, 10, 7, 8, 8, 9, 7,
8, 9, 10, 10, 8, 8, 9, 7, 10, 8,
4, 6, 5, 4, 3, 7, 5, 6, 4, 5,
8, 7, 8, 6, 9, 7, 8, 8, 10, 8) #<1>
knowledge <- c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0) #<2>
format <-c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1) #<3>
kadai <- tibble(score, knowledge, format) %>% #<4>
mutate(knowledge = factor(knowledge,
levels = c(1, 0),
labels = c("high", "low")),
format = factor(format,
levels = c(1, 0),
labels = c("new", "normal")))
```
::: content-hidden
## 解答例(コードのみ)
```{r}
lm(score ~ format * knowledge, data = kadai) |>
Anova()
ggline(data = kadai,
x = "format",
y = "score",
color = "knowledge",
add = c("mean")) +
theme_ggdist()
```
##
:::
## うりぼーネットで授業振り返りアンケートに回答してください!
{fig-align="center" width="887"}
# 参考文献 {.nunumbered}
::: #refs
:::