---
title: "13 コストドライバとKPIの分析"
author: 佐久間智広
date: 2024/07/05
format:
html: default
revealjs:
output-file: 13_kpi_slide.html
---
## はじめに {data-name="はじめに"}
今回扱う内容はKey Performance Indicator (KPI) 分析です
KPI
: Performance(主に収益)を予測する指標
コストドライバーと似てるっちゃ似てますが,Balanced Scorecardのような戦略的業績測定システムの運用を助けるようなイメージの分析を扱います。\
\
### 戦略的業績測定システム
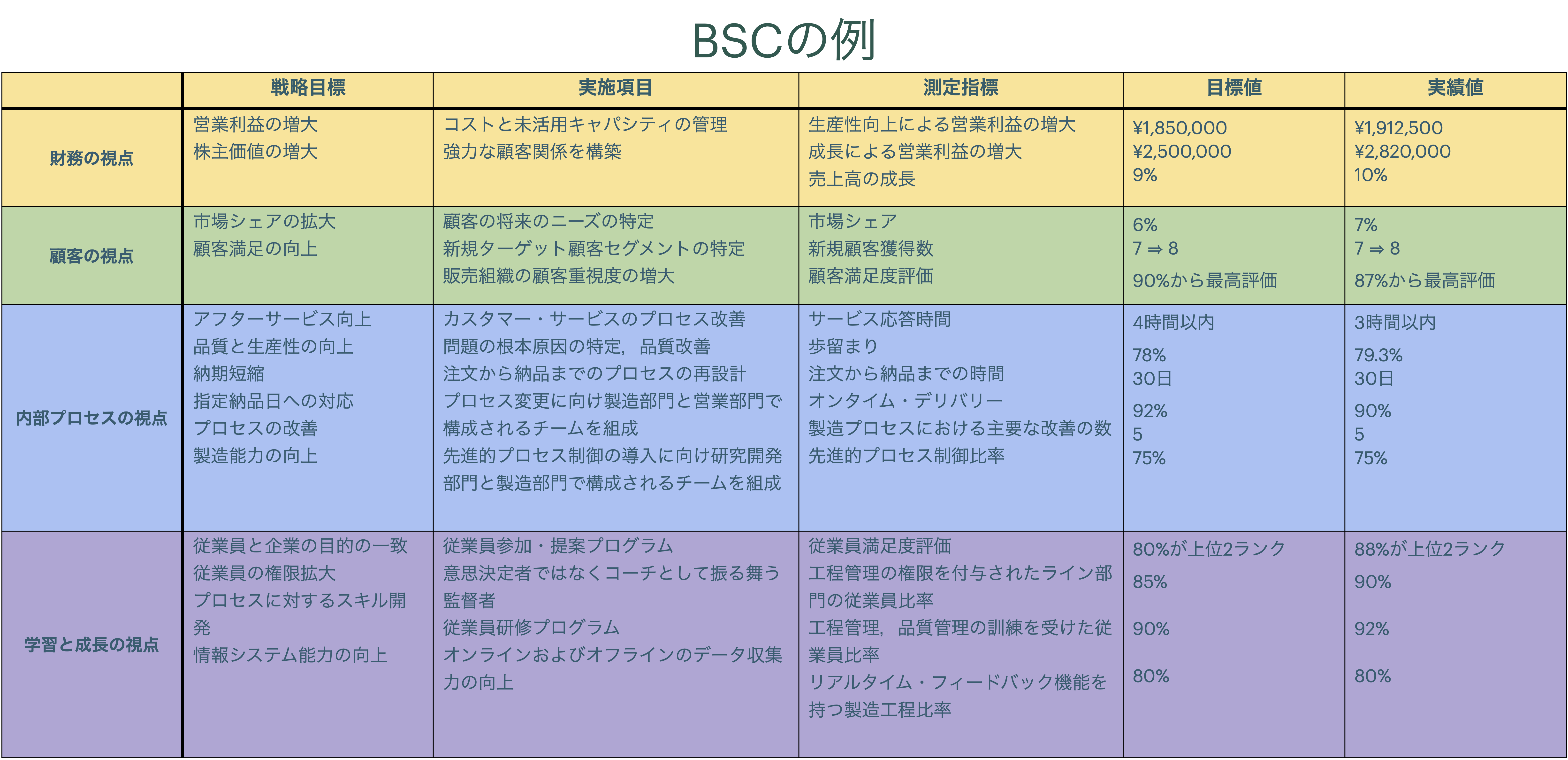
経営戦略実現のために,財務的指標(売上高や原価,利益など)だけでなく,非財務指標(顧客満足度・従業員満足度・生産効率・従業員の学習成果など)を盛り込んだ多元的な業績測定・評価を行う仕組み。代表的なものがBalanced Scorecard(BSC)
## BSC(Balanced Scorecard:バランスト・スコアカード)とは {data-name="BSC"}
端的に言うと
- 「[測定できなければ管理できない]{.green}」と言う精神のもと
- 財務指標だけでは測れない業務における多様な側面を非財務的な複数の指標で測定し
- 多面的に測定・評価しよう
という取り組み。複数の視点を4つの視点に整理

------------------------------------------------------------------------
------------------------------------------------------------------------
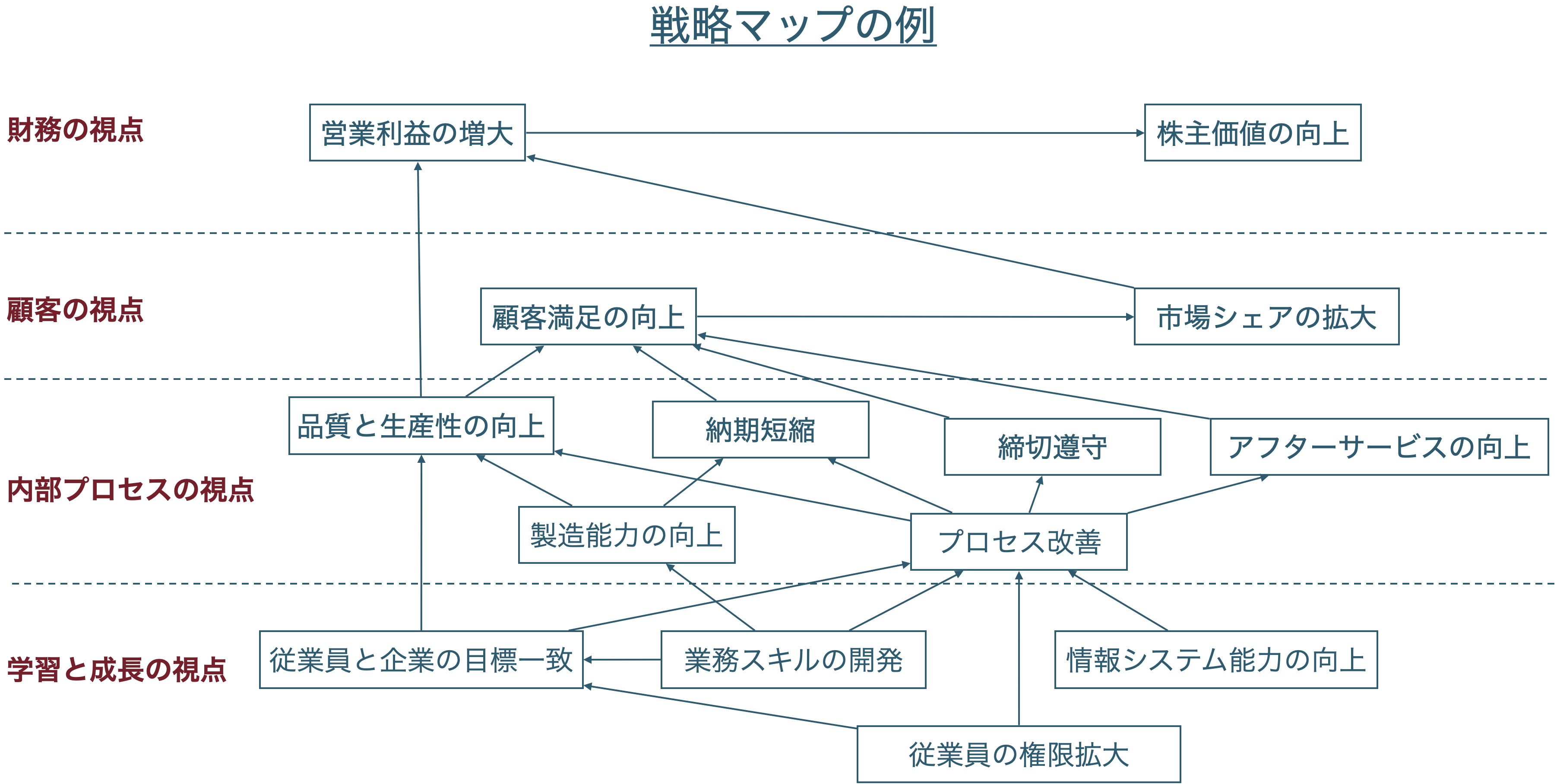
### 戦略マップ
BSCで設定される指標間に想定される因果関係を図示したのが戦略マップ
------------------------------------------------------------------------
### 期待される効果
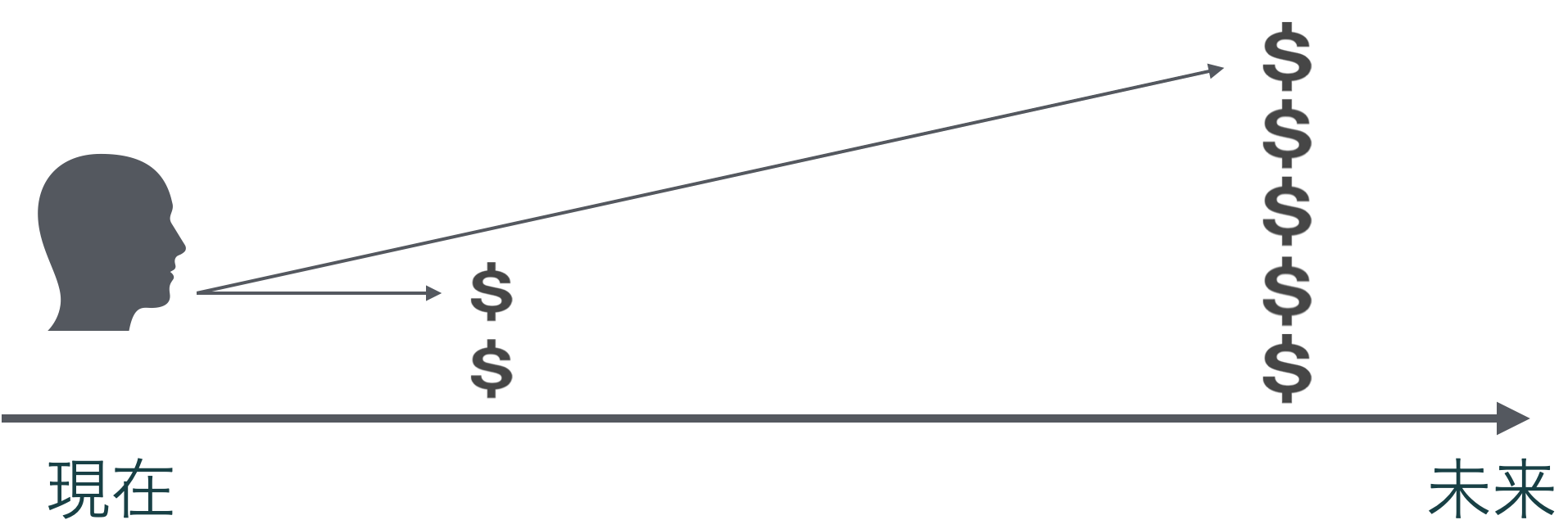
#### 短期志向の緩和
会計業績は通常1年,半年,4半期などの単位で集計
会計数値を目標として業務を行うと,比較的短期の業績を高くするために行動をとるように
- 言い換えると,長期的な視点が欠如する
- もっとひどい場合は長期的業績を犠牲にして短期的業績をとりに行くような行動をとる
BSCでは,より長期的な視野を持った指標(顧客→社内プロセス→育成と行くほど長期的な視点に立っています)を管理指標とすることで,短期思考を軽減することが期待される
{fig-align="center" width="1185"}
------------------------------------------------------------------------
#### 多面的な業績評価
財務指標は従業員たちが企業の目的に沿った行動をとっているかどうかを把握する指標としては不完全
- 例えばチームワークよく働けるような気配りや,部下のフォロー,アドバイスとった行動は,企業の目的達成に資する行動だけど,財務指標では測定しづらい
BSCを用いることで,このような会計情報だけでは把握しにくい企業の貢献を多面的な指標によって汲み取れることが期待される
- BSCなどの多面的業績評価システムが業績を改善するということは数多くの研究で報告されている [@lee2011; @chenhall2005; @hyvonen2007; @vanderstede2006]。
------------------------------------------------------------------------
#### 指標間の因果関係を意識した行動の変容
::: columns
::: {.column width="50%"}
「顧客満足は大事」,「従業員満足は大事」,「利益目標の達成は大事」など大事なことは様々
- それら大事なものを会計指標にこだわらず数値化して管理する,というのがBSC
- 戦略マップと併用することで,大事なもの同士の関係が明示される
:::
::: {.column width="50%"}
{fig-align="center" width="375"}
:::
:::
## 戦略的業績測定システム運用上の困難性 {data-name="困難性"}
BSCをはじめとする戦略的業績測定システムは,
- 多様な指標を組み合わせて使う
ことを想定し,暗黙的に,もしくは明示的に
- 指標間の因果関係を想定
します。
{fig-align="right" width="993"}
------------------------------------------------------------------------
::: columns
::: {.column width="70%"}
理想的には,因果関係が本当に存在するのかどうかを定期的に確認し,改善していくことが望まれる
しかし,この指標間の因果関係を実際に検証するのはすごく難しいです。
:::
::: {.column width="30%"}
{fig-align="right" width="249"}
:::
:::
{fig-align="center" width="1474"}
------------------------------------------------------------------------
結果として…
- 間違った目標に向けて努力
- 結果に繋がらない

------------------------------------------------------------------------
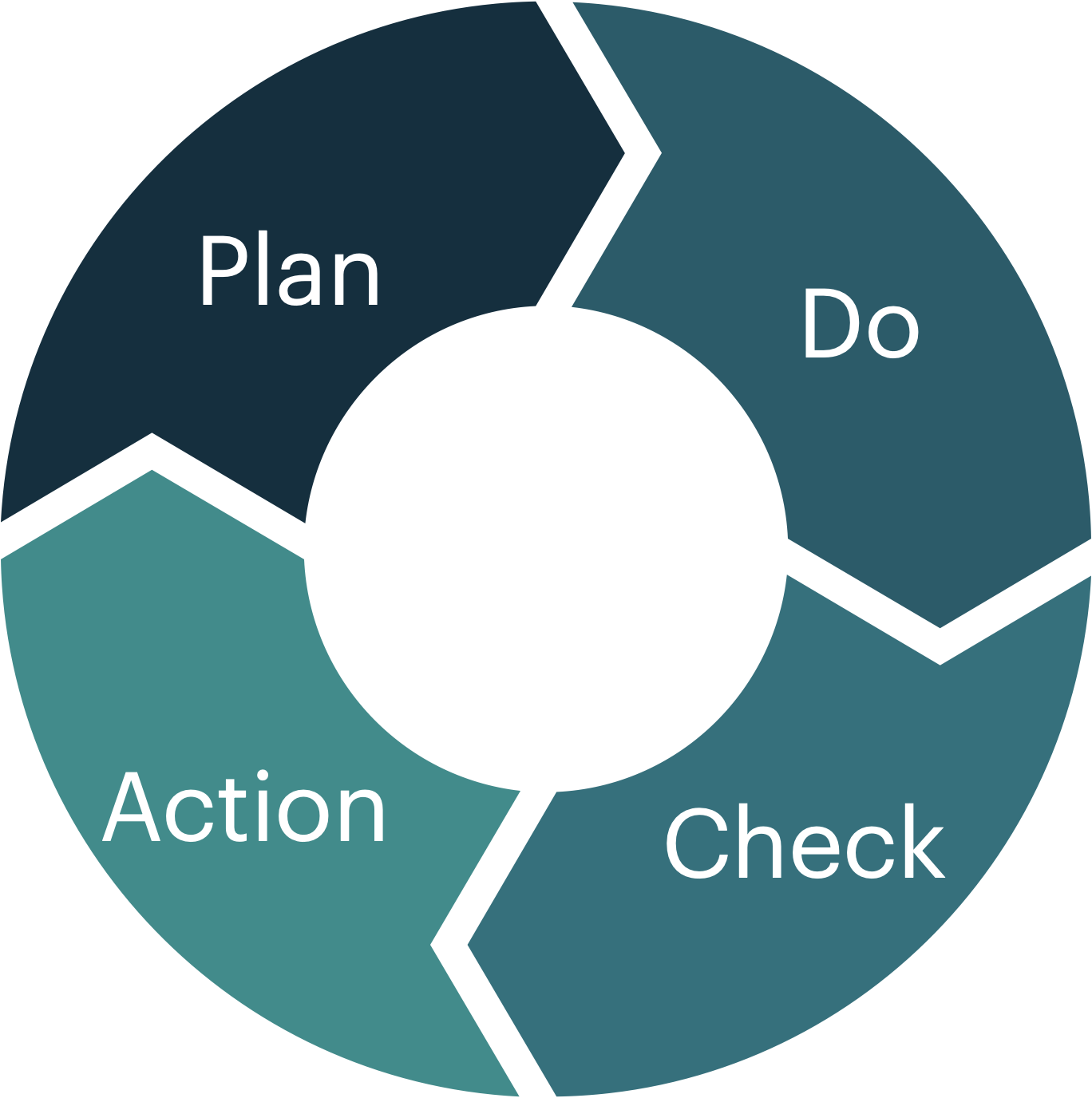
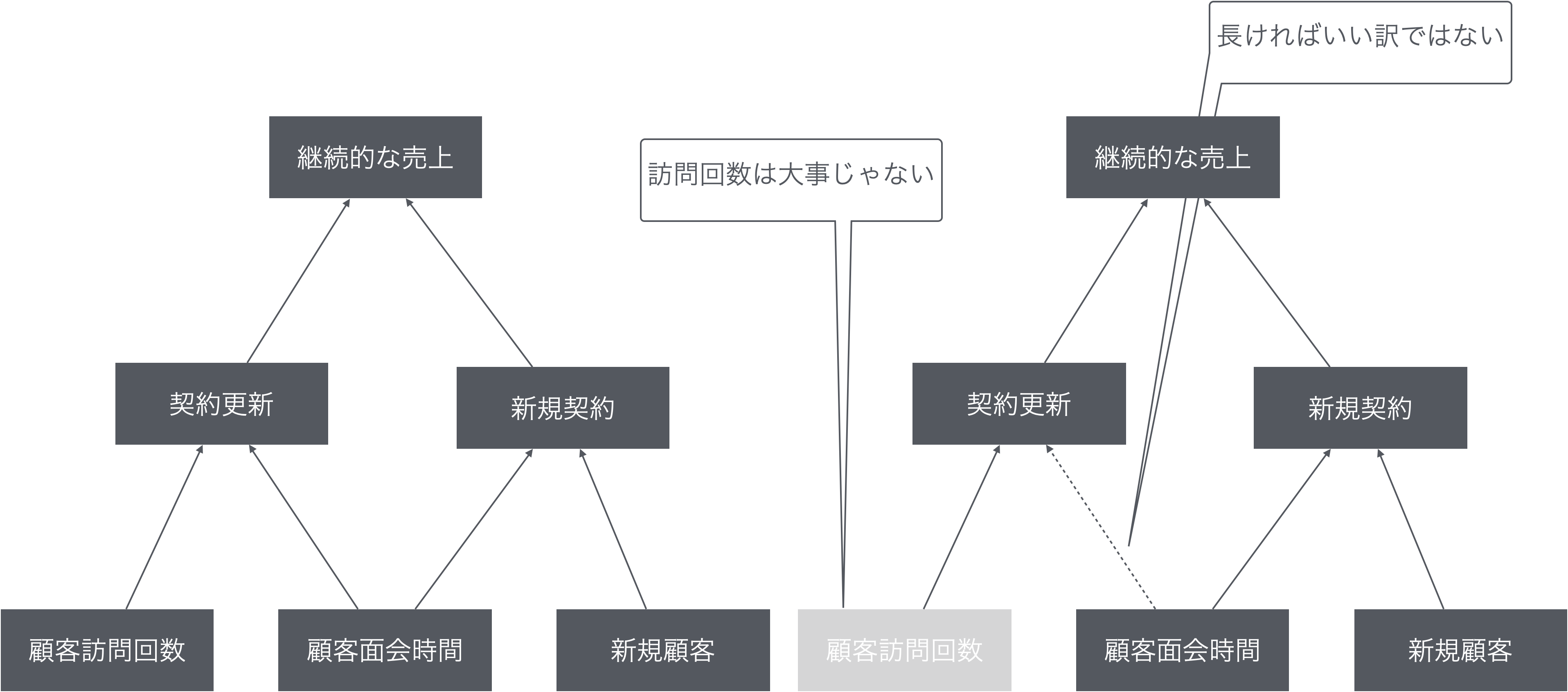
### そもそも何が難しいのか?
1. **根本的に因果関係を推定するのは難しい**
最近因果推論の研究者がノーベル経済学賞を取っている(2021年)ように,データから因果関係を明らかにする手法は発展している。でも難しい。
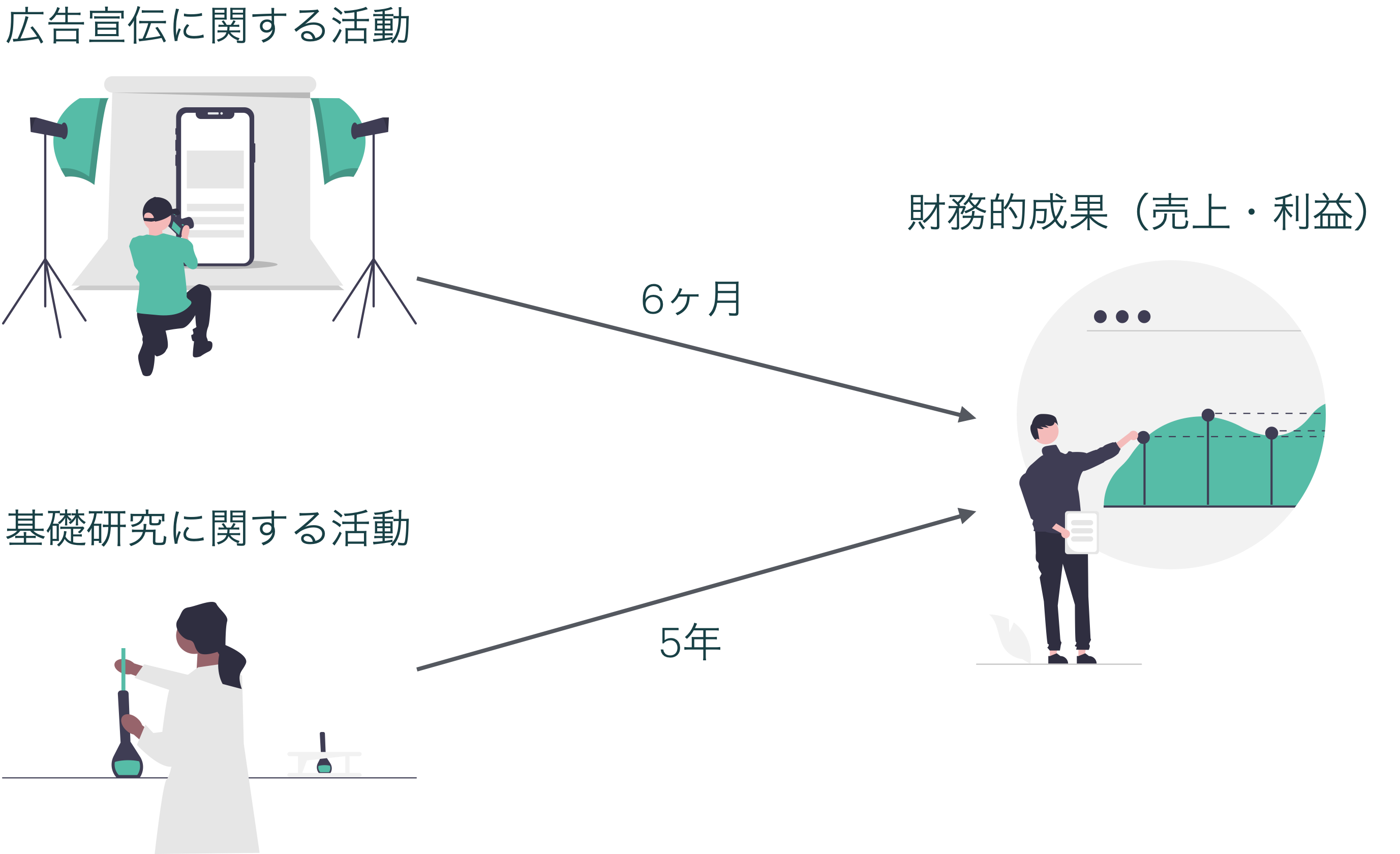
2. **各関係は異なるタイムラグを持つかもしれない**
{width="984"}
------------------------------------------------------------------------
3. **非財務指標と財務指標との間の関係は線形ではないかもしれない**
例えば,最高品質を目指すことは収益につながるのか?
- ある程度以上を超えたら十分,みたいなラインはないのか?
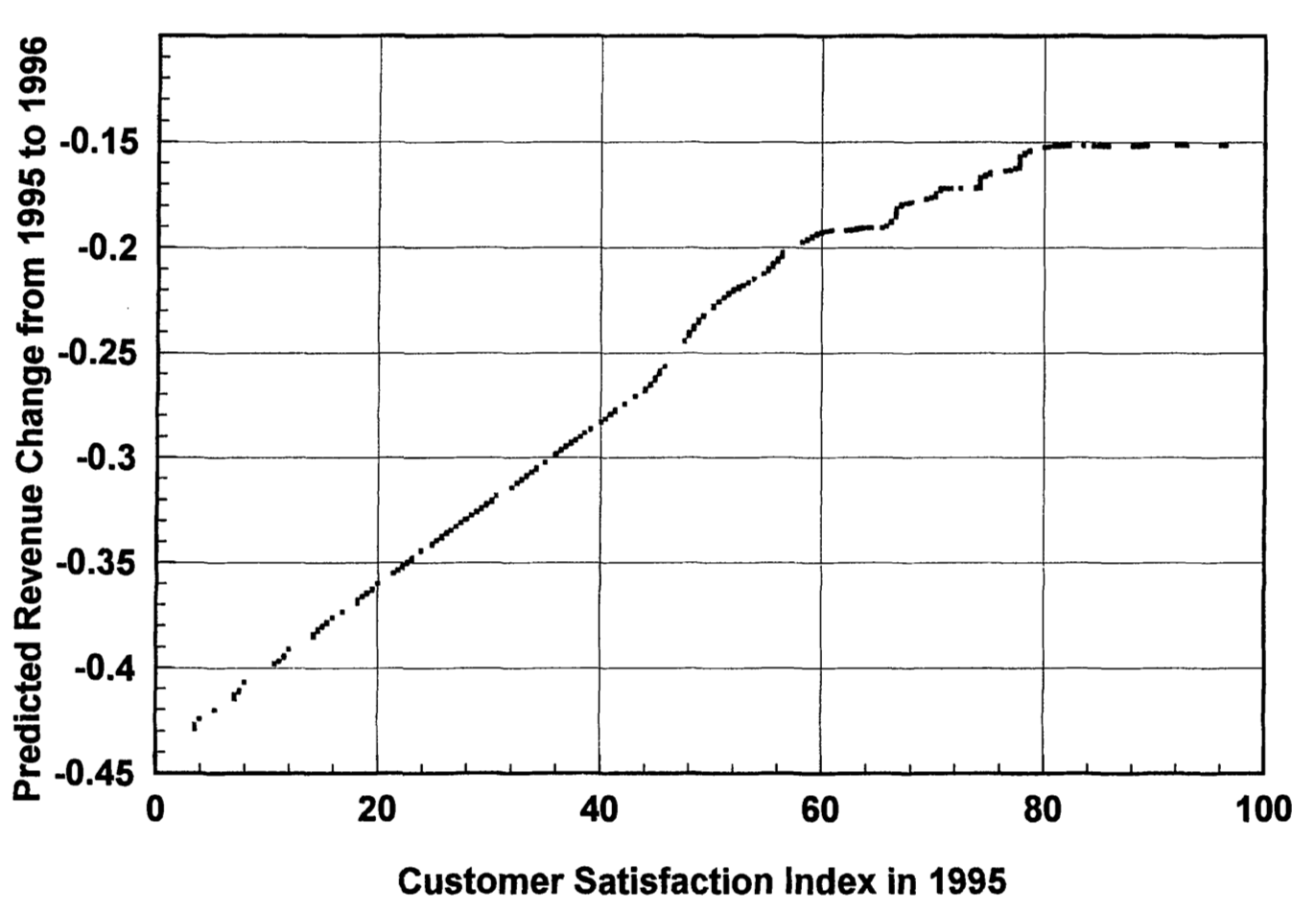
::: {.callout-note icon="false"}
## @ittner1998
アメリカの通信会社の顧客満足データと財務データを使って,満足度と収益変化の非線形な関係を発見。
{fig-align="center" width="721"}
:::
## 今日やること {data-name="やること"}
というような背景を踏まえて,今日は
::: box
::: center
タイムラグなどを考慮したKPIとPの関係の検証
:::
:::
について扱います。
### 準備 {.unnumbered}
```{r}
#| code-summary: パッケージの読み込み
options(digits = 3)
if (!require("pacman")) install.packages("pacman")
pacman::p_load(tidyverse, magrittr, estimatr,
modelsummary, here, broom, conflicted,
lmtest, zoo, tinytable, np, glmnet)
conflicts_prefer(dplyr::group_by(),
dplyr::select(),
dplyr::filter(),
dplyr::arrange(),
dplyr::lag())
```
```{r}
set.seed(123)
adv <- 100 + 10 * rnorm(106) |> round(digits = 1)
rd <- 60 + 10 * rnorm(106,0, 0.4) |> round(digits = 1)
sales <- numeric(106)
kpi <- tibble(sales, adv, rd)
kpi <- kpi |>
mutate(sales = 800 + 2 * adv + 3 * lag(adv) + 3 * lag(rd, 2) +
3 * lag(rd, 3) + 25 * rnorm(106) |>
round(digits = 1))
write_csv(kpi, here('data', '13_kpi.csv'))
```
------------------------------------------------------------------------
## 例1 {data-name="例1"}
### 状況
ある企業の経営者は,広告宣伝活動と研究開発活動それぞれが収益と関係していると予測し,それぞれの活動にヒトや資金を投入してきました。実際それぞれの活動が収益とどのように関係しているのかを知りたいと考えています。
### データ
```{r}
kpi <- here('data', '13_kpi.csv') |> read_csv()
kpi
```
------------------------------------------------------------------------
### 記述統計量
::: columns
::: {.column width="50%"}
#### 記述統計表
`datasummary()`関数を使うと結構簡単
```{r}
datasummary(sales + adv + rd ~ Mean + SD + Min + Max,
data = kpi)
```
:::
::: {.column width="50%"}
#### 相関表
相関表も同じように
```{r}
kpi |>
datasummary_correlation()
```
:::
:::
売上と広告宣伝活動との相関はあるが,rdとの関係はあまりなさそう
------------------------------------------------------------------------
### 回帰分析
#### 単純な回帰分析
::: columns
::: {.column width="70%"}
```{r}
m01 <- lm(sales ~ adv, data = kpi)
m02 <- lm(sales ~ rd, data = kpi)
m03 <- lm(sales ~ adv + rd, data = kpi)
msummary(list(m01, m02, m03),
stars = TRUE,
gof_omit = 'Log.Lik.|BIC|RMSE',
align = 'lccc'
)
```
:::
::: {.column width="30%"}
広告宣伝活動は関係あるけど研究は関係なさそう。
ということは,研究活動は無駄だから削減するべき?
:::
:::
------------------------------------------------------------------------
再掲
2. **各関係は異なるタイムラグを持つかもしれない**
{fig-align="center" width="1148"}
------------------------------------------------------------------------
#### advのタイムラグ
advについて,異なるタイムラグを含めて推定してみる
```{r}
m1 <- lm(sales ~ adv , data = kpi)
m2 <- lm(sales ~ adv + lag(adv) , data = kpi)
m3 <- lm(sales ~ adv + lag(adv) + lag(adv, 2) , data = kpi)
m4 <- lm(sales ~ adv + lag(adv) + lag(adv, 2) + lag(adv, 3), data = kpi)
results <- list(m1, m2, m3, m4 )
msummary(results,
stars = TRUE,
coef_map = c('(Intercept)',
'adv',
'lag(adv)',
'lag(adv, 2)',
'lag(adv, 3)',
'lag(adv, 4)'),
gof_omit = 'Log.Lik.|RMSE') |>
style_tt(
i = 13:15,
background = "teal",
color = "white",
bold = TRUE)
```
------------------------------------------------------------------------
#### R and Dのタイムラグ
同様に研究開発もやってみる。
```{r}
m5 <- lm(sales ~ rd , data = kpi)
m6 <- lm(sales ~ rd + lag(rd) , data = kpi)
m7 <- lm(sales ~ rd + lag(rd) + lag(rd, 2) , data = kpi)
m8 <- lm(sales ~ rd + lag(rd) + lag(rd, 2) + lag(rd, 3), data = kpi)
m9 <- lm(sales ~ rd + lag(rd) + lag(rd, 2) + lag(rd, 3) + lag(rd, 4), data = kpi)
m10 <- lm(sales ~ rd + lag(rd) + lag(rd, 2) + lag(rd, 3) + lag(rd, 4) + lag(rd, 5), data = kpi)
m11 <- lm(sales ~ rd + lag(rd) + lag(rd, 2) + lag(rd, 3) + lag(rd, 4) + lag(rd, 5) + lag(rd, 6), data = kpi)
resultsr <- list(m5, m6, m7, m8, m9, m10, m11)
msummary(resultsr,
stars = TRUE,
gof_omit = 'Log.Lik.|RMSE') |>
style_tt(
i = 19:21,
background = "teal",
color = "white",
bold = TRUE)
```
------------------------------------------------------------------------
#### タイムラグの決め方
非財務指標が財務業績に影響を与えるまでにタイムラグを持ちうることは知られているが,どれぐらいのタイムラグを持つかを事前に予測することは難しい [@banker2000] 。
モデルのラグを決める方法としては決定係数やAICやBICといった情報量規準が使われる [@banker2000; @banker2005]
AIC
: 赤池情報量規準。赤池さんが作った。パラメータを増やせば増やすだけモデルの当てはまり(決定係数も)がよくなるけれど,そのサンプルのみに適合するような結果(過学習)が起こる場合も。\
$AIC=-2\log L+2(k+1)$**\
**Lは尤度。kはパラメータの数。第1項は尤度のマイナスなので,**小さければ小さい方が良い**。第2項は説明変数を増やすと大きくなる。説明変数が増えることによる第1項の減少と,第2項の増加のバランスを探るイメージ?
BIC
: $BIC=-2\log L+k \log n$。考え方は一緒で小さい方が良い。
でも,今回はモデル全体の当てはまりというよりは,広告宣伝が売上にどれぐらいのタイムラグで効くと考えればいいのか知りたい。なので,**係数の有意性**の方が役に立つかも。
- 今期と前期が効いてる
係数の全体の有意性はF検定で検証される
------------------------------------------------------------------------
### 結果の検討
- 広告宣伝は,直近1,2年の業績と関係
- 一方で研究開発は3,4年後に効いてくる
- 直近の業績だけを使うと,研究開発と業績は関係なしと出てしまう
などなど…
## 例2 {data-name="例2"}
### 状況
Y社は,顧客満足度をKPIとして設定し,その向上に取り組んできた。満足した顧客のリピート利用により収益が向上する,という想定をしている。
実際に毎月収集している顧客満足度データと収益データを組み合わせてその関係を分析してみたい。
```{r}
#| echo: false
# データ生成のためのパラメータ
set.seed(123) # 乱数シードの設定
n <- 24 # 24ヶ月分のデータ
# 月次の顧客満足度(0から100の範囲)
satisfaction <- runif(n, 60, 100)
# 収益の生成(満足度が90%を超えると収益に効果がなくなる非線形関係を反映)
revenue <- numeric(n)
for (i in 2:n) {
revenue[i] <- ifelse(satisfaction[i-1] <= 90,
-0.1 * (satisfaction[i-1] - 90)^2 + 1000 + rnorm(1, 0, 10),
-0.1 * (90 - 90)^2 + 1000 + rnorm(1, 0, 10))
}
revenue[1] <- 1000 + rnorm(1, 0, 10) # 初月の収益(適当に設定)
# データフレームの作成
data <- tibble(month = 1:n, satisfaction = satisfaction, revenue = revenue)
write_csv(data, here('data', '13_kpi2.csv'))
```
データ
```{r}
kpi2 <- here('data', '13_kpi2.csv') |> read_csv()
kpi2
```
------------------------------------------------------------------------
### 記述統計量
#### 記述統計表と相関表
```{r}
#| label: tbl-kpi2
#| tbl-cap: 記述統計量
#| tbl-subcap:
#| - 記述統計表
#| - 相関表
datasummary(satisfaction + revenue ~ Mean + SD + Min + Max,
data = kpi2)
kpi2 |>
datasummary_correlation()
```
------------------------------------------------------------------------
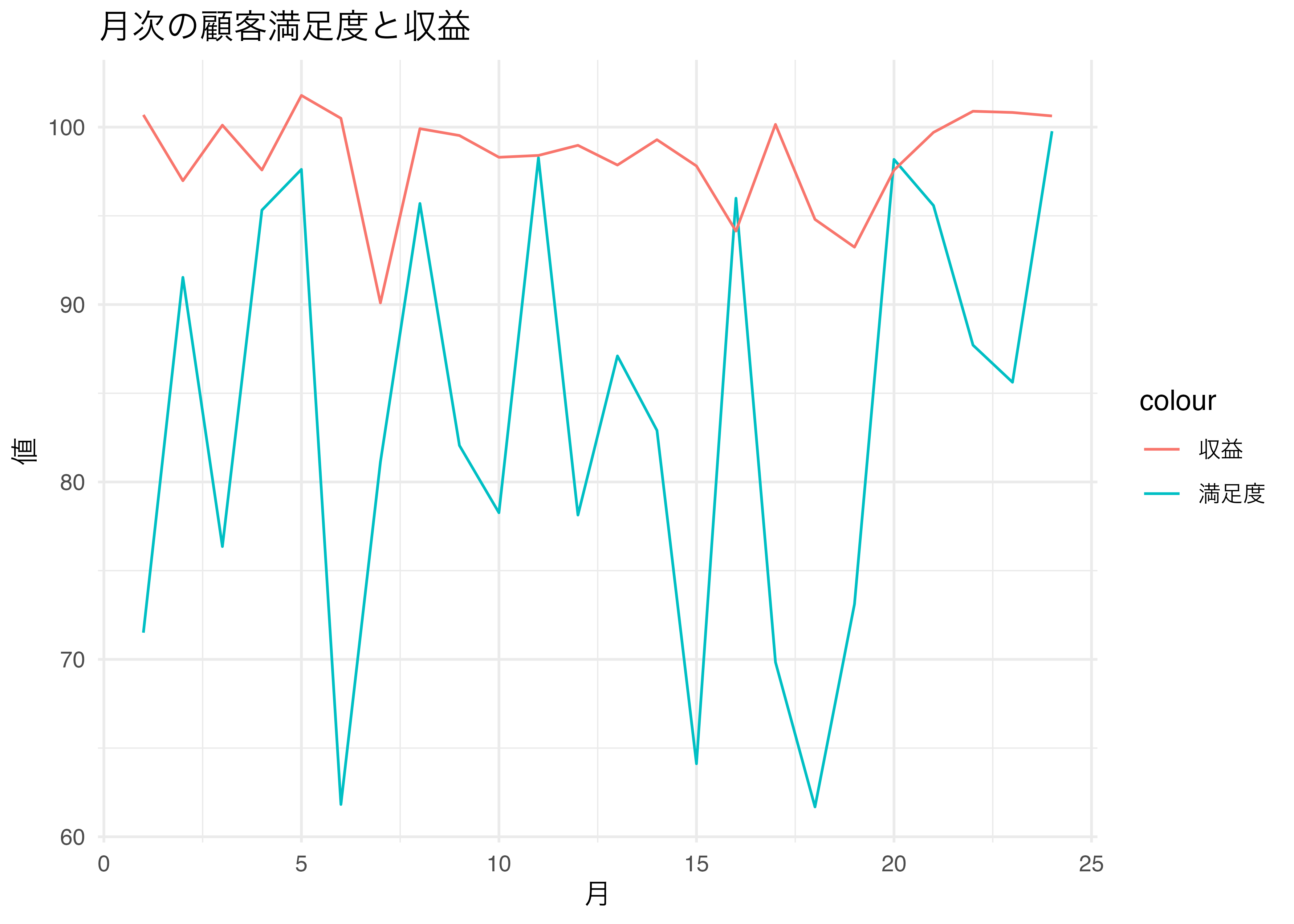
#### 時系列グラフ
```{r}
# データのプロット
ggplot(kpi2, aes(x = month)) +
geom_line(aes(y = satisfaction, color = "満足度")) +
geom_line(aes(y = revenue / 10, color = "収益")) + # 収益のスケールを調整
labs(title = "月次の顧客満足度と収益",
x = "月",
y = "値") +
theme_minimal()
```
満足度と収益の間にはタイムラグがありそう。1ヶ月程度。
------------------------------------------------------------------------
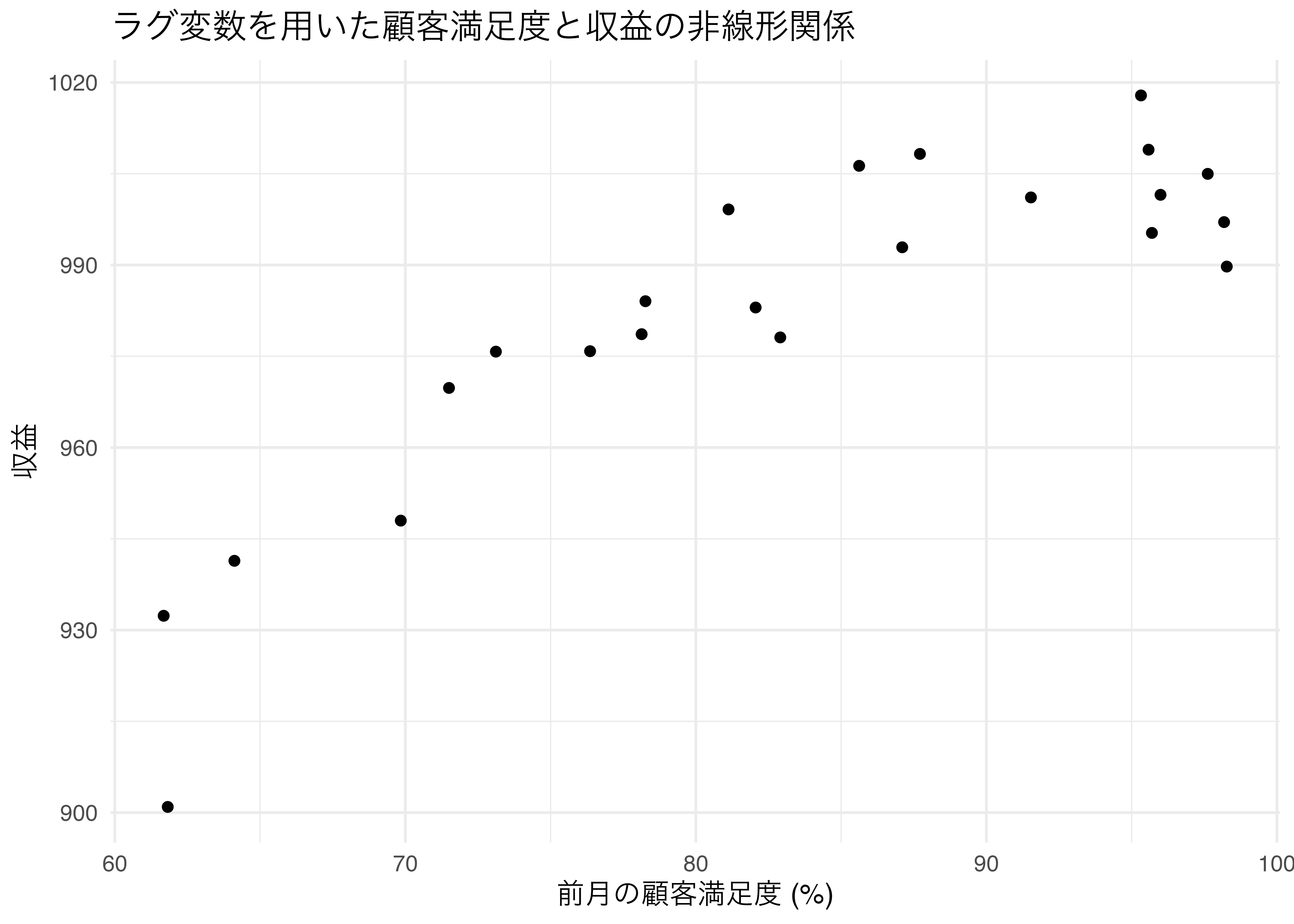
```{r}
# ラグ変数の作成
kpi2 <- kpi2 %>%
mutate(lagged_satisfaction = lag(satisfaction, 1))
ggplot(kpi2, aes(x = lagged_satisfaction, y = revenue)) +
geom_point() +
labs(title = "ラグ変数を用いた顧客満足度と収益の非線形関係",
x = "前月の顧客満足度 (%)",
y = "収益") +
theme_minimal()
```
微妙だけど,顧客満足度がある程度以上高いとき,収益は伸びていなさそう
------------------------------------------------------------------------
```{r}
#| label: tbl-kpi2-2
#| tbl-cap: 記述統計量
#| tbl-subcap:
#| - 記述統計表
#| - 相関表
datasummary(satisfaction + lagged_satisfaction + revenue ~
Mean + SD + Min + Max,
data = kpi2)
kpi2 |>
datasummary_correlation()
```
前月の満足度と収益に強い相関関係がある
------------------------------------------------------------------------
### 分析
#### 非線形関係の表現
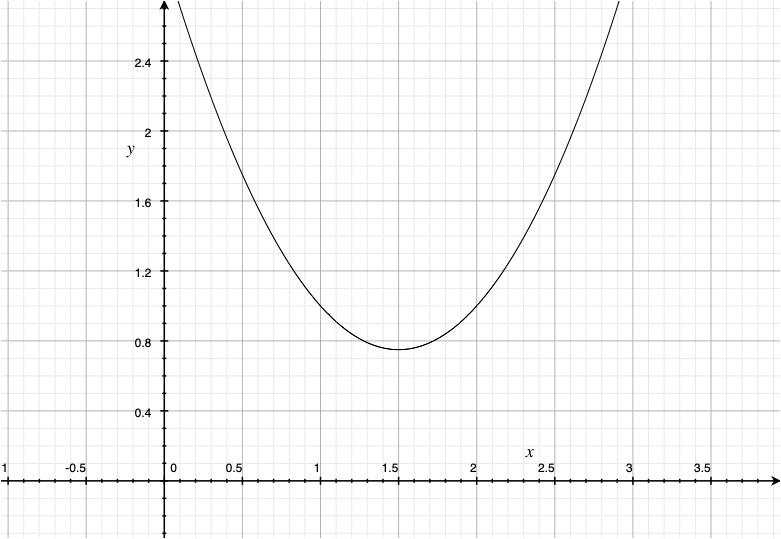
線形回帰モデルでは,独立変数の高次の項目を入れることで非直線の関係をモデル化できる
$$
y_i = \beta_0 + \beta_1 x_i + \beta_2 x^2_i + e_i
$$ {#eq-one}
@eq-one は $x$の二次関数とみることができる。
- $\beta_2$が正だとUの形,負だと放物線の形
Rでは,高次の項を含めるときには以下のように表現する
``` r
lm(y ~ x + I(x^2))
```
::: {layout="[1,1]"}
{width="435"}
{width="435"}
:::
------------------------------------------------------------------------
::: columns
::: {.column width="70%"}
```{r}
m0 <- lm(revenue ~ lagged_satisfaction, data = kpi2)
m1 <- lm(revenue ~ lagged_satisfaction + I(lagged_satisfaction^2), data = kpi2)
m2 <- lm(revenue ~ lagged_satisfaction + I(lagged_satisfaction^2)+ I(lagged_satisfaction^3), data = kpi2)
# モデルの要約
list(m0, m1, m2) |>
modelsummary(stars = TRUE,
gof_omit = 'Log.Lik.|RMSE')
```
:::
::: {.column width="30%"}
- 二次関数のモデル2が良さそう
- 決定係数,AIC,BIC,係数の有意性
- 二次の項が有意に負→放物線の形
:::
:::
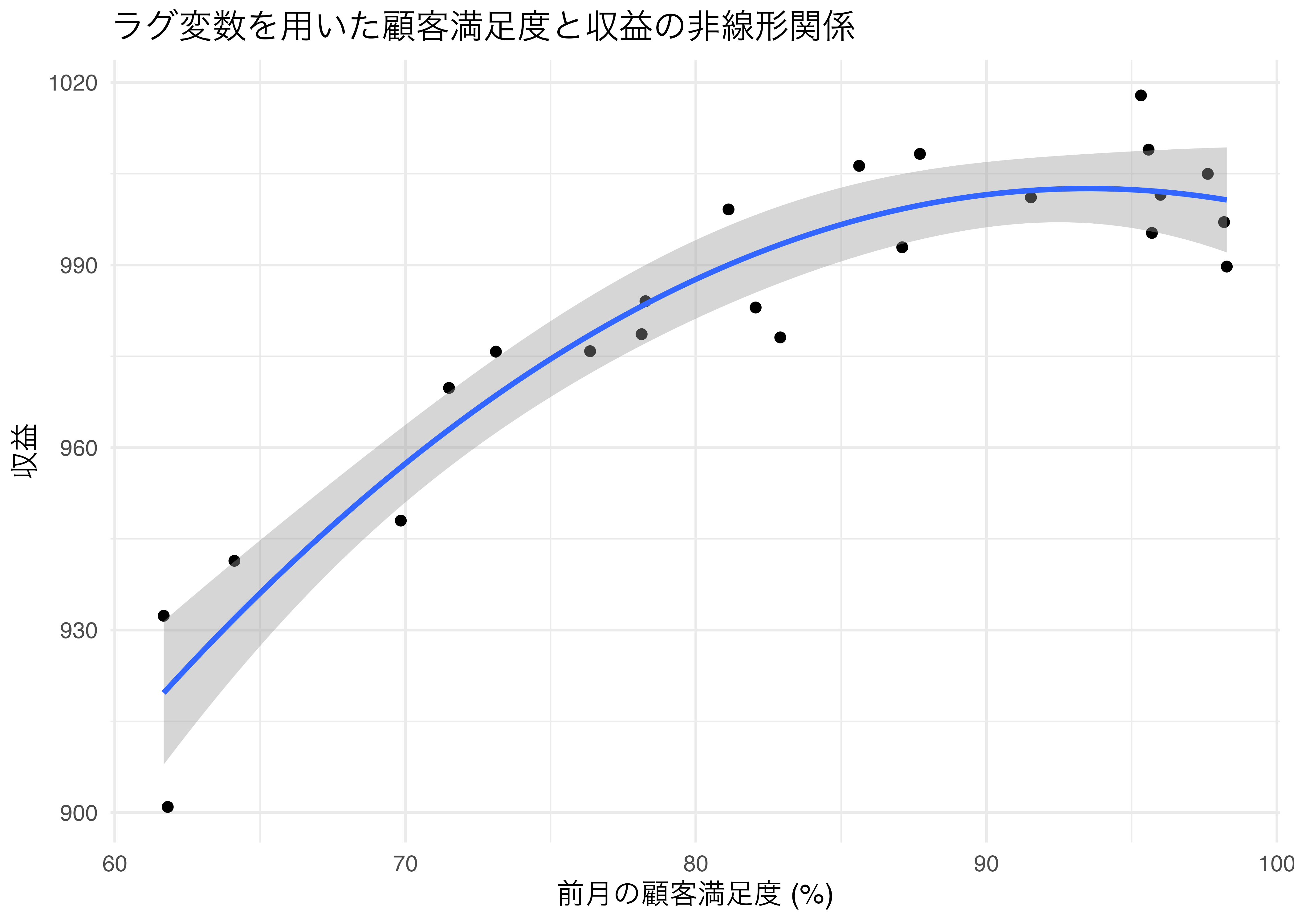
```{r}
# モデルの適合度を確認するためのプロット
ggplot(kpi2, aes(x = lagged_satisfaction, y = revenue)) +
geom_point() +
stat_smooth(method = "lm", formula = y ~ x + I(x^2)) +
labs(title = "ラグ変数を用いた顧客満足度と収益の非線形関係",
x = "前月の顧客満足度 (%)",
y = "収益") +
theme_minimal()
```
#### 他のモデルとの比較
```{r}
# ラグなしの線形モデル
model1 <- lm(revenue ~ satisfaction, data = kpi2)
# ラグなしの非線形モデル(2次関数)
model2 <- lm(revenue ~ satisfaction + I(satisfaction^2), data = kpi2)
# ラグを含む線形モデル
model3 <- lm(revenue ~ lagged_satisfaction, data = kpi2)
# ラグを含む非線形モデル(2次関数)
model4 <- lm(revenue ~ lagged_satisfaction + I(lagged_satisfaction^2), data = kpi2)
# ラグなしとラグありの変数を両方含むモデル
model5 <- lm(revenue ~ satisfaction + I(satisfaction^2) + lagged_satisfaction + I(lagged_satisfaction^2), data = kpi2)
# 各モデルの結果を表にまとめる
models <- list(
"線形モデル(ラグなし)" = model1,
"非線形モデル(ラグなし)" = model2,
"線形モデル(ラグあり)" = model3,
"非線形モデル(ラグあり)" = model4,
"複合モデル(ラグなし+ラグあり)" = model5
)
modelsummary(models,
stars = TRUE,
gof_omit = 'Log.Lik.|RMSE',
title = "顧客満足度と収益の関係モデル比較")
```
------------------------------------------------------------------------
### 結果の検討
- 顧客満足度は,翌月の売上を予測する
- 顧客満足度と売上の関係は単純な直線関係ではない
- 90%付近から先は売上高の向上のつながらない
- 90%程度の満足度を目指すのが効率的?
## まとめ {data-name="まとめ"}
- 財務指標と非財務指標を組み合わせて業績測定・管理することで,財務指標だけを用いた場合に予測される問題を緩和できる(戦略的業績測定システム)
- 通常非財務指標は,財務指標の先行指標として,将来業績につながることが期待される中間的成果を測定
- 理想的には非財務指標と財務指標との関係を定期的に検証し,場合によっては指標の選択や目標レベルを修正したい
- でも,タイムラグや非線形の関係などを特定して両者の関係を検証することは結構難しい
- 関係性を検証せずに使うことで,戦略的業績測定システムに期待された効果が発揮されないことも
## 課題 {data-name="課題"}
経営上重要だと思われるインプットとアウトプットの関係を分析する際,今回扱ったようなタイムラグもしくは非線形の関係を想定した方が良さそうだと考えられる例を,なぜそう考えたのか,という理由とともに一つ挙げてください。
(授業で使った例以外で)
- BEEF+の**第13回(2024/07/05)課題**に記入してください。
## 参考文献 {.unnumbered}
::: {#refs}
:::