8 規模効果の検証を例とした線形ファクター・モデル入門

1 ポートフォリオ・ソート（教科書第6.1.2節）

1.1 時価総額によるポートフォリオ・ソート

• 何らかの特性に基づき各銘柄を順位付けて，その順位に基づいてポートフォリオを構築することをポートフォリオ・ソートと呼ぶ．

目標

• ここではその例として前年度末の時価総額に応じて投資ユニバース¹を十等分し，その実現リターンを比較してみよう．

---

1.2 (Step 1) 月次データch05_output1.csvと年次データch05_output1.csvの読み込み

Code

pacman::p_load(tidyverse, broom) 

monthly_data <- read_csv("../simulation_data/ch05_output1.csv")

Rows: 95040 Columns: 25
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (25): year, month, month_ID, firm_ID, stock_price, DPS, shares_outstandi...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Code

annual_data  <- read_csv("../simulation_data/ch05_output2.csv")

Rows: 7920 Columns: 18
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (18): firm_ID, year, R, Re, R_F, industry_ID, sales, OX, NFE, X, OA, FA,...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

---

1.3 (Step 2) 前年度末の時価総額lagged_MEを追加すると共に，年度ごとにME_rank10という変数名で十分位に振り分け

Code

annual_data <- annual_data %>% 
  group_by(firm_ID) %>% # firm_IDでグループ化
  mutate(lagged_ME = lag(ME)) %>% # 前年度末の時価総額を定義
  ungroup() %>% 
  group_by(year) %>% # 年ごとにグループ化
  mutate(ME_rank10 = as.factor(ntile(lagged_ME, 10))) %>% # ntile()関数を用いて十個のグループに分類
  ungroup()

• 時価総額が小さい方から順に1から10までを割り振るために，dplyrのntile()関数を用いてME_rank10という変数を作成している．
• ntile()関数は，最初の引数としてグループ分けしたいデータ（ここではlagged_ME）を取り，その次の引数にグループの数（ここでは10）を取る．
  • ちなみに，十分位はdecile，五分位はquintile，四分位はquartile，三分位はtertileという．
• ntile()関数の返り値は自然数型となるので，上のコードではas.factor()関数によりそれをファクター型に変更している．

---

1.4 (Step 3) 各ポートフォリオに属する企業数を確認

Code

annual_data %>% 
  select(year, firm_ID, ME_rank10) %>% 
  drop_na() %>% # 欠損行を削除
  group_by(year, ME_rank10) %>% # yearとME_rank10でグループ化
  summarize(N = n()) %>% # 各ポートフォリオの企業数をカウント
  ungroup()

`summarise()` has grouped output by 'year'. You can override using the
`.groups` argument.

# A tibble: 50 × 3
    year ME_rank10     N
   <dbl> <fct>     <int>
 1  2016 1           125
 2  2016 2           124
 3  2016 3           124
 4  2016 4           124
 5  2016 5           124
 6  2016 6           124
 7  2016 7           124
 8  2016 8           124
 9  2016 9           124
10  2016 10          124
# ℹ 40 more rows

---

1.5 (Step 4) full_join()関数を用いてmonthly_dataと結合

• 以下のコードでは，yearとfirm_IDをキーにしてmonthly_dataと結合すると共に，drop_na()関数により欠損データを除いている．

Code

annual_data %>%
  select(year, firm_ID, ME_rank10) %>% # 年次データから追加したい情報を抽出
  full_join(monthly_data, by = c("year", "firm_ID")) %>% # yearとfirm_IDをキーに月次データと結合
  drop_na() # 欠損行を削除 

# A tibble: 76,848 × 26
    year firm_ID ME_rank10 month month_ID stock_price   DPS shares_outstanding
   <dbl>   <dbl> <fct>     <dbl>    <dbl>       <dbl> <dbl>              <dbl>
 1  2017       1 2             1       25        3797     0            2422000
 2  2017       1 2             2       26        4859     0            2422000
 3  2017       1 2             3       27        4371     0            2422000
 4  2017       1 2             4       28        4082     0            2906000
 5  2017       1 2             5       29        3478     0            2906000
 6  2017       1 2             6       30        4317    43            2906000
 7  2017       1 2             7       31        4441     0            2906000
 8  2017       1 2             8       32        4746     0            2906000
 9  2017       1 2             9       33        4690     0            2906000
10  2017       1 2            10       34        4369     0            2906000
# ℹ 76,838 more rows
# ℹ 18 more variables: adjustment_coefficient <dbl>, R_F <dbl>, ME <dbl>,
#   lagged_stock_price <dbl>, R <dbl>, Re <dbl>, industry_ID <dbl>,
#   sales <dbl>, OX <dbl>, NFE <dbl>, X <dbl>, OA <dbl>, FA <dbl>, OL <dbl>,
#   FO <dbl>, BE <dbl>, lagged_BE <dbl>, ROE <dbl>

---

1.6 (Step 5) 各月・各ポートフォリオごとに実現超過リターンを計算

• ポートフォリオ\(P\)に属する\(N\)銘柄に対して，同金額配分する（すなわち，100万円を5銘柄に配分する場合は，各銘柄に対する投資金額は20万円であり，各々の保有割合は20%である）場合を考えよう．このような考え方で保有割合を決定したポートフォリオのことを等加重ポートフォリオ (equal-weighted portfolio)と呼ぶ．
• 等加重ポートフォリオを前提にした場合，月次\(t\)におけるポートフォリオ\(P\)の実現超過リターン\(R_{P,t}^{e}\)は，以下のように計算することができ，各銘柄の超過リターンの単純平均を取れば計算可能であることが分かる．

\[ R_{P,t}^{e} = \frac{1}{N} R_{1,t}^{e} + \frac{1}{N} R_{2,t}^{e} + \cdots + \frac{1}{N} R_{N,t}^{e} = \frac{\sum_{j = 1}^{N} R_{j,t}^{e}}{N} \]

---

1.7 各月・各ポートフォリオの実現超過リターンを計算し，そのデータフレームをME_sorted_portfolioと名付けよう

Code

ME_sorted_portfolio <- annual_data %>%
  select(year, firm_ID, ME_rank10) %>% # 年次データから追加したい情報を抽出
  full_join(monthly_data, by = c("year", "firm_ID")) %>% # yearとfirm_IDをキーに月次データと結合
  drop_na() %>% # 欠損行を削除 
  group_by(month_ID, ME_rank10) %>% # month_IDとME_rank10に関してグループ化
  summarize(Re = mean(Re)) %>% # 各グループで月次超過リターンの平均値を計算
  ungroup()

`summarise()` has grouped output by 'month_ID'. You can override using the
`.groups` argument.

Code

head(ME_sorted_portfolio)

# A tibble: 6 × 3
  month_ID ME_rank10     Re
     <dbl> <fct>      <dbl>
1       13 1         0.0291
2       13 2         0.0272
3       13 3         0.0353
4       13 4         0.0545
5       13 5         0.0460
6       13 6         0.0438

---

1.8 各ポートフォリオの平均超過リターンを棒グラフにより可視化してみよう！

Code

ME_sorted_portfolio %>% 
  group_by(ME_rank10) %>% # ME_rank10に関してグループ化
  summarize(mean_Re = mean(Re)) %>% # 月次超過リターンの平均値を計算
  ggplot() + 
  geom_col(aes(x = ME_rank10, y = mean_Re)) + # 棒グラフを描くにはgeom_col()関数を用いる
  labs(x = "ME Rank", y = "Mean Monthly Excess Return") + 
  scale_y_continuous(expand = c(0, 0)) + 
  theme_classic()

---

1.9 なぜこのようなシステマティックな現象が観察されるのか？

• CAPMが正しい \(\Rightarrow\) ME_rank10が小さい企業ほど，マーケット・ベータが高いので，平均的に超過リターンが高い傾向にある．
• もし，上記が当てはまらないのであれば，CAPMは現実データを適切に描写しない誤ったモデルである可能性が高い．

---

2 CAPMの実証的な検証（教科書第6.2節）

2.1 CAPMの概要（再掲）

二つの命題

• （第一命題） 市場ポートフォリオは接点ポートフォリオと一致し，効率的フロンティア（資本市場線）上に位置する．
• （第二命題） 各証券のリスクプレミアムは，その証券のマーケット・ベータに比例する．

\[ \begin{align*} \underbrace{\mathbb{E}\left[R_i\right]-R_F}_{\textbf{証券$i$のリスクプレミアム}} & =\underbrace{\beta_i}_{\textbf{証券$i$のマーケット・ベータ}}\underbrace{\left(\mathbb{E}\left[R_M\right]-R_F\right)}_{\textbf{市場リスクプレミアム}}\\ \text{ただし，}\quad \beta_i & =\frac{{\rm Cov}[R_i,\ R_M]}{{\rm Var}[R_M]} \end{align*} \]

2.2 その世界では，マーケット・ベータこそ全て（再掲）

• 第二命題は期待値に関する主張なので，実際に観察されるリターンはこれに誤差項\(\varepsilon_{i,t}\)が加わったものと考えることができる．

\[ \begin{align} \underbrace{R_{i,t}}_{\textbf{証券$i$の実現リターン}} - \underbrace{R_{F,t}}_{\textbf{無リスク金利}} & = \beta_i(\underbrace{R_{M,t}}_{\substack{\textbf{市場ポートフォリオの} \\ \textbf{実現リターン}}} - \underbrace{R_{F,t}}_{\textbf{無リスク金利}}) +\varepsilon_{i,t}\nonumber\\ \underbrace{R_{i,t}^e}_{\textbf{証券$i$の実現超過リターン}} & = \beta_i\underbrace{R_{M,t}^e}_{\substack{\textbf{市場ポートフォリオの} \\ \textbf{実現超過リターン}}} +\varepsilon_{i,t} \label{eq:CAPM1} \tag{6.1} \end{align} \]

• 表記をシンプルとするため，\(R_{i,t}^e\)という記号を用いたが，これは\(t\)期における証券\(i\)の無リスク金利に対する実現超過リターン\(R_{i,t}-R_{F,t}\) を意味する．

---

2.3 誤差項の仮定（再掲）

ここで，\(\varepsilon_{i,t}\)に関して以下の仮定を置こう．\(\mathbb{E}\)

1. \(\varepsilon_{i,t}\)は独立同一分布に従う
2. \(\mathbb{E}[\varepsilon_{i,t}] = 0\)
3. \(\mathbb{E}[R_{M,t}^e \varepsilon_{i,t}] = 0\)

• このように定式化すると，CAPMの実証的な検証は線形回帰に帰着させることができる．つまり，超過リターンの時系列データを用意し，個別銘柄の超過リターンを市場ポートフォリオのそれで線形回帰する．
• その際の回帰係数がマーケット・ベータである．

---

2.4 CAPMの実証的な検証

• CAPMは任意の資産に成立するものであり，個別銘柄の組合せであるポートフォリオにも応用できる．以降では，先に作成した時価総額で十等分したポートフォリオを検証対象としよう．
• これらのポートフォリオのリターンを次の回帰モデルで説明することを考える．

\[ \begin{align} R_{P,t}^e=\underbrace{\alpha_{P}}_{\substack{\textbf{CAPMが成立} \\ \textbf{すればゼロ}}} + \beta_{P}R_{M,t}^e+\varepsilon_{P,t} \label{eq:CAPM2} \tag{6.2} \end{align} \]

---

2.5 (\(\ref{eq:CAPM1}\))式と(\(\ref{eq:CAPM2}\))式の相違点

1. (\(\ref{eq:CAPM1}\))式と比べてみると，ポートフォリオ\(P\)が対象となるため，従属変数を証券\(i\)の実現超過リターン\(R_{i,t}^e\)からポートフォリオ\(P\)の実現超過リターン\(R_{P,t}^e\)へ，また，回帰係数と誤差項についても，証券\(i\)のものからポートフォリオ\(P\)のものへと置き換えている．
2. より本質的な違いとして，(\(\ref{eq:CAPM2}\))式には定数項\(\alpha_{P}\)が登場している点に注意しよう．CAPMが成立する世界では，超過リターンが唯一マーケット・ベータのみで説明できるので，定数項は不要である．しかし，ここではCAPMが実証的に成立しているかを検証したいので，CAPMが成立しない可能性を考慮して\(\alpha_{P}\)も回帰モデルに組み込んでいる．

• もし実際に推定された\(\hat{\alpha}_{P}\)がゼロではないとすると，それはCAPMが実証的に成立していない証拠となる．この定数項\(\alpha_{P}\)は，CAPMを前提にした値であることを強調するため，CAPMアルファと呼ばれる．

---

2.6 ME_Rank10が1のポートフォリオのみを対象とした検証

まずは下準備として，市場ポートフォリオの超過リターンが収録されたch06_output.csvをfactor_dataとして読み込み，month_IDをキーにME_sorted_portfolioと結合し，市場ポートフォリオの超過リターンR_Meを追加したのが以下のコードである．

Code

# ファクター・データの読み込み
factor_data <- read_csv("../simulation_data/ch06_output.csv")

Rows: 60 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (6): month_ID, R_F, R_M, R_Me, SMB, HML

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Code

# 市場ポートフォリオの超過リターンを追加
ME_sorted_portfolio <- factor_data %>% 
  select(-R_F) %>% # 無リスク金利は重複するので結合前に削除
  full_join(ME_sorted_portfolio, by = "month_ID") %>% # month_IDをキーに
  select(-R_Me, R_Me) # R_Meを最終列へ移動

head(ME_sorted_portfolio)

# A tibble: 6 × 7
  month_ID    R_M      SMB     HML ME_rank10     Re   R_Me
     <dbl>  <dbl>    <dbl>   <dbl> <fct>      <dbl>  <dbl>
1       13 0.0458 -0.00178 0.00200 1         0.0291 0.0458
2       13 0.0458 -0.00178 0.00200 2         0.0272 0.0458
3       13 0.0458 -0.00178 0.00200 3         0.0353 0.0458
4       13 0.0458 -0.00178 0.00200 4         0.0545 0.0458
5       13 0.0458 -0.00178 0.00200 5         0.0460 0.0458
6       13 0.0458 -0.00178 0.00200 6         0.0438 0.0458

---

2.7 時系列回帰 — 概要

• ここでは手始めに時価総額が最小のポートフォリオ (ME_rank10が1)のデータのみを抽出して，(\(\ref{eq:CAPM2}\))式を推定してみよう．これ時系列回帰 (time-series regression)といって，個々の銘柄やポートフォリオの実現リターンが市場ポートフォリオのリターンによってどの程度説明できるかを回帰したモデルである．
• 時系列回帰のイメージは，下の図のとおりであり，任意のポートフォリオ\(P\)に関して，\(x\)軸には市場ポートフォリオの月次超過リターンを，\(y\)軸にはポートフォリオ\(P\)の月次超過リターンを取ったものである．

---

2.8 時系列回帰 — OLSの実行

Code

ME_sorted_portfolio %>% 
  filter(ME_rank10 == 1) %>% # 時価総額が最小のポートフォリオを抽出
  lm(Re ~ R_Me, data = .) %>% # .を使ってlm()関数の第二引数にデータを代入
  tidy() # 線形回帰の結果をtidy()関数でデータフレームに変換

# A tibble: 2 × 5
  term        estimate std.error statistic       p.value
  <chr>          <dbl>     <dbl>     <dbl>         <dbl>
1 (Intercept)   0.0121   0.00404      3.00 0.00395      
2 R_Me          0.654    0.0976       6.70 0.00000000937

• 推定結果を見てみると，マーケット・ベータはR_Meの回帰係数として0.654と推定されており，このポートフォリオが市場ポートフォリオと正に相関していることが確認できる．
• 続いて，CAPMアルファを見てみると，推定値は(Intercept)の0.0121であり，対応する\(t\)値は3.00と表示されている，したがって，CAPMアルファがゼロと等しいという帰無仮説は，有意水準1%で棄却されるため，少なくともこのデータにおいてはCAPMが成立していない可能性が高いと言える．

---

2.9 for文を用いた全ポートフォリオの推定

目標

• 先のコード群では，時価総額が最小のポートフォリオを例に(\(\ref{eq:CAPM2}\))式の推定方法を学んだが，ここではfor文を用いて，全てのポートフォリオについて同様の推定を行ってみよう．

---

2.10 目標を実現するためのコード

• 下のコードで定義したCAPM_resultsはリストであり，推定結果を閲覧するにはその各要素にアクセスする必要がある．異なるポートフォリオ間で推定結果を比較するには，各データフレームを一つのデータフレームに統合する方が便利である．それを実現するには，dplyrのbind_rows()関数を用いる．今回のように二つ以上のデータフレームを一つに結合したい場合に重宝する．

Code

# 推定結果を保存するために空のリストを準備
CAPM_results <- list(NA) 

for(i in 1:10){
  CAPM_results[[i]] <- ME_sorted_portfolio %>% 
    filter(ME_rank10 == i) %>%
    lm(Re ~ R_Me, data = .) %>%
    tidy() %>% 
    mutate(ME_rank10 = as.factor(i)) %>% # 推定対象のポートフォリオ名を保存
    select(ME_rank10, everything()) # ME_rank10を第一列に移動
}

# 複数のデータフレームを一つに統合
binded_CAPM_results <- bind_rows(CAPM_results)
head(binded_CAPM_results)

# A tibble: 6 × 6
  ME_rank10 term        estimate std.error statistic  p.value
  <fct>     <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 1         (Intercept)   0.0121   0.00404      3.00 3.95e- 3
2 1         R_Me          0.654    0.0976       6.70 9.37e- 9
3 2         (Intercept)   0.0106   0.00375      2.83 6.44e- 3
4 2         R_Me          0.711    0.0908       7.83 1.19e-10
5 3         (Intercept)   0.0120   0.00312      3.86 2.90e- 4
6 3         R_Me          0.770    0.0754      10.2  1.42e-14

---

2.11 各ポートフォリオのCAPMアルファの可視化

• 最後に，定数項に関する推定結果のみをfilter()関数により抽出し，棒グラフにより各十分位ポートフォリオのCAPMアルファを描画してみよう．

Code

binded_CAPM_results %>% 
  filter(term == "(Intercept)") %>% # 定数項に関する推定結果のみを抽出
  ggplot() +
  geom_col(aes(x = ME_rank10, y = estimate)) + # 横軸をME_rank10, 縦軸をCAPM_alphaとする棒グラフ
  geom_hline(yintercept = 0) + 
  labs(x = "ME Rank", y = "CAPM alpha") + 
  scale_y_continuous(limits = c(-0.003, 0.013)) +
  theme_classic()

• 出力結果を見てみると，時価総額が小さいポートフォリオほど，CAPM_alphが高いということが分かる．特に時価総額が最も小さいポートフォリオのCAPMアルファは1.21%で，年率に換算すると14.52% (\(=1.21% \times 12\))にもなる．
• したがって，先に確認した実現超過リターンの傾向は，マーケット・ベータを調整済みのCAPMアルファでも存在することが分かる．

---

3 線形ファクター・モデルの導入（教科書第6.3節）

3.1 線形ファクター・モデルの概要

• ファイナンス理論の歴史において，様々なCAPMの拡張・修正が提案されてきたが，その多くが線形ファクター・モデルという部類に属する．

線形ファクター・モデルとは？

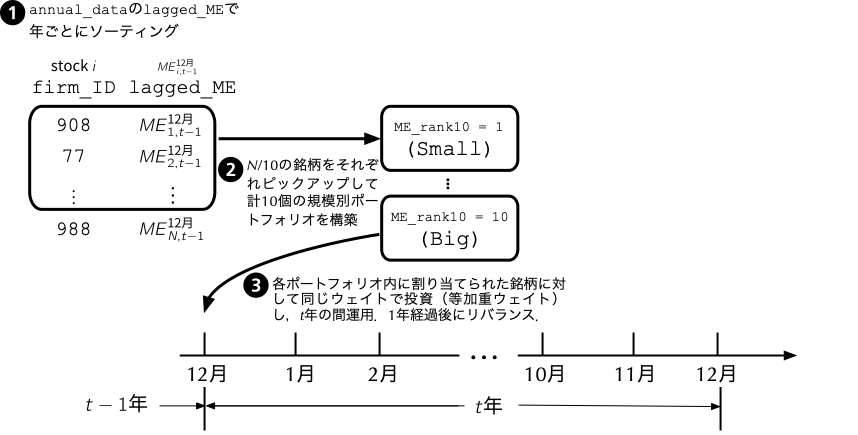
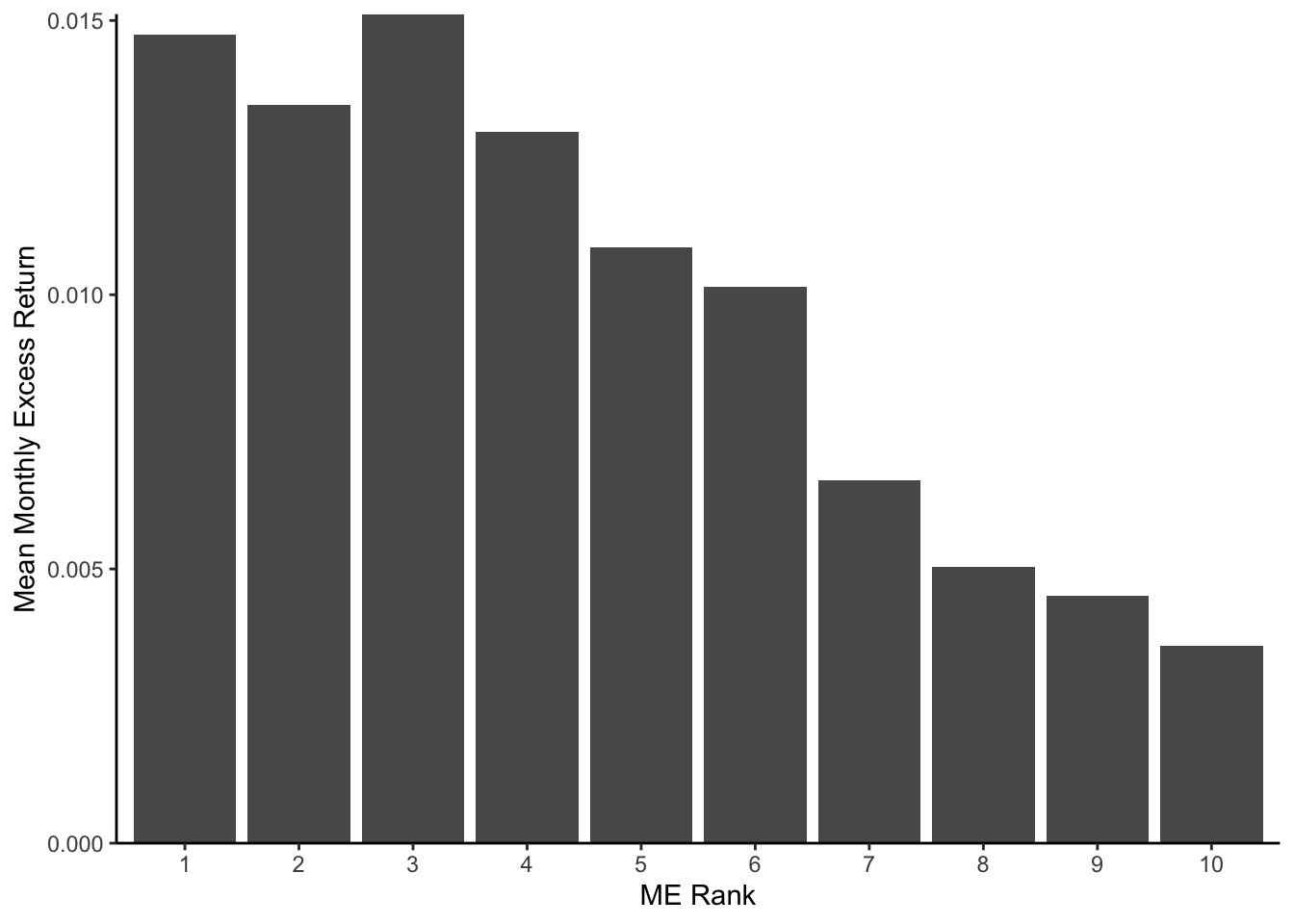
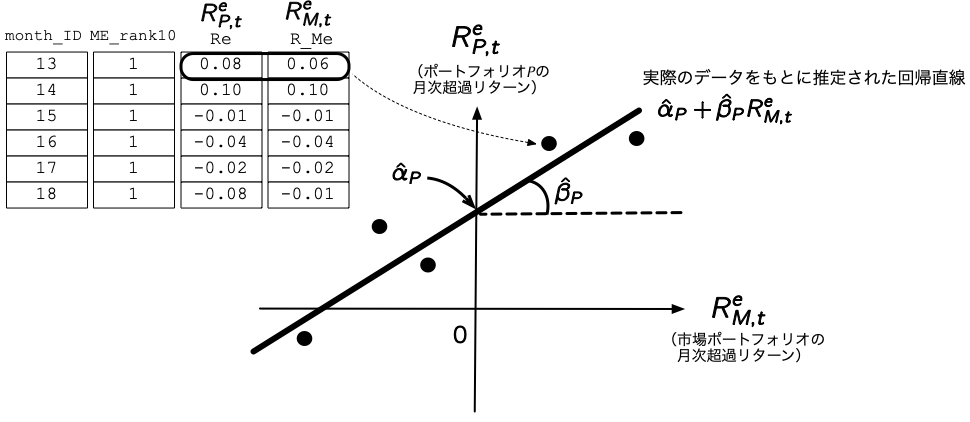
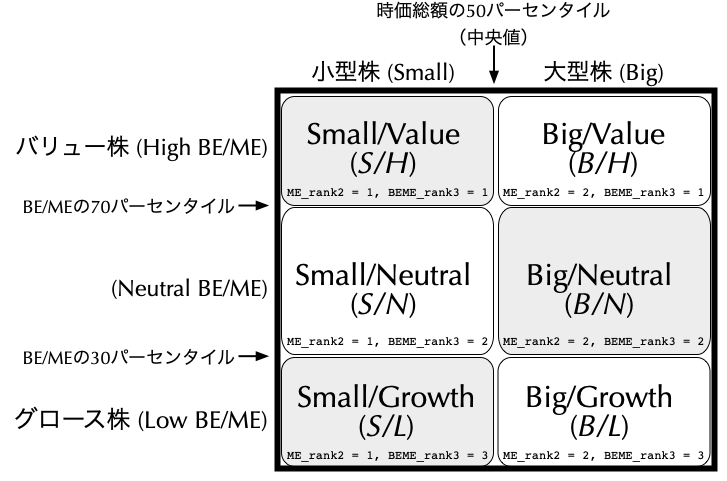
任意の証券の無リスク金利に対する超過リターンが，ファクターと呼ばれる\(K\)個の確率変数\(F^k\) (\(k = 1, 2, \ldots, K\))，及び誤差項\(\varepsilon_{i}\)の線形結合で記述できるというモデルである． \[ \begin{align*} R_{i,t}^e = \beta_i^1 F_t^1+\beta_i^2 F_t^2+\cdots + \beta_i^K F_t^K + \varepsilon_{i,t} \end{align*} \]

ただし，誤差項\(\varepsilon_{i}\)は\(\mathbb{E}[\varepsilon_{i}]=0\)，かつ\({\rm Cov}[\varepsilon_{i}, F^k]=0\)を満たす．ここで，\(\beta_i^k\)はファクター・ローディング (factor loading)と呼ばれ，証券\(i\)のリターンとファクター\(F^k\)との共変動の強さを表すパラメータであり，説明変数を一つから複数へと増やした重回帰分析によって推定することができる．ただし，通常の回帰分析と異なり，定数項を除いている点がポイントである．

• CAPMも線形ファクター・モデルの一種であり，\(K = 1\)かつ\(F_t^1 = R_{M,t}-R_{F,t}\)と書ける．

---

3.2 Fama-Frenchの3ファクター・モデル

• 「CAPMだけで観察されたリターンを説明しようとすると，小型株やバリュー株がアルファを持つ」というCAPMアノマリーが数多くの実証研究によって報告されていた．
• Fama-Frenchの3ファクター・モデル（以降では，FF3モデルと略）は，それらをモデルに取り込むために，(1) 市場ポートフォリオの超過リターン\(R_{M}^e\)に加えて，(2) サイズ・ファクター\(\mathit{SMB}\)と(3) バリュー・ファクター\(\mathit{HML}\)を追加したモデルである． \[ \begin{align} R_{i,t}^e=\beta_i^MR_{M,t}^e+\beta_i^{\mathit{SMB}}{\mathit{SMB}}_t+\beta_i^{\mathit{HML}}{\mathit{HML}}_t+\varepsilon_{i,t} \label{eq:FF3} \tag{6.3} \end{align} \]
• 実際に\(\mathit{SMB}\)と\(\mathit{HML}\)の両者を計算するには，銘柄ユニバースを次スライドの図のように六分割する．
• ここで横軸は時価総額の中央値を境に二分割されており，左に小型株が，右に大型株が分類される．一方，縦軸はBE/MEの30%，70%分位点を境に三分割されており，上にバリュー株が，下にグロース株が分類される．こうして時価総額とBE/MEの違いによって異なった特性を持つ六つのサブポートフォリオが構築されることになる．

---

3.3 6 size-BE/MEポートフォリオ

• 月次\(t\)の\(\mathit{SMB}\)を表す\(\mathit{SMB}_{t}\)は，次のように計算することができる． \[ \begin{align*} \mathit{SMB}_{t} = \underbrace{\left(\frac{\mathit{S/H}_{t}+\mathit{S/N}_{t}+\mathit{S/L}_{t}}{3}\right)}_{\textbf{小型株の平均リターン (\textcolor{red}{Small})}}-\underbrace{\left(\frac{\mathit{B/H}_{t}+\mathit{B/N}_{t}+\mathit{B/L}_{t}}{3}\right)}_{\textbf{大型株の平均リターン (\textcolor{red}{Big})}} \end{align*} \] ただし，右辺の各項は月次\(t\)における各ポートフォリオの月次リターンであり，例えば，\(\mathit{S/H}_{t}\)は\(\mathit{S/H}\)ポートフォリオの時価総額加重平均リターンを表す．
• 他方，月次\(t\)の\(\mathit{HML}\)を表す\(\mathit{HML}_{t}\)は，次のように計算することができる． \[ \begin{align*} \mathit{HML}_{t} = \underbrace{\left(\frac{\mathit{S/H}_{t}+\mathit{B/H}_{t}}{2}\right)}_{\textbf{バリュー株の平均リターン (\textcolor{blue}{High BE/ME})}}-\underbrace{\left(\frac{\mathit{S/L}_{t}+ \mathit{B/L}_{t}}{2}\right)}_{\textbf{グロース株の平均リターン (\textcolor{blue}{Low BE/ME})}} \end{align*} \]

---

3.4 FF3アルファ

目標

• CAPMを前提としてアルファを推定したが，ここでは，CAPMに代わってFF3モデルに基づくアルファ（以下では，FF3アルファと略称）を推定しよう．
• CAPMを前提とすれば，時価総額に基づく十分位ポートフォリオのいくつかでは統計的にも有意なアルファが観察されたが，FF3モデルを前提とすれば，アルファは消滅するか否かを検証するのが目的である．
• この検証のために利用する回帰モデルは，次式のとおりである． \[ \begin{align} R_{P,t}^e = {\alpha_P^{\mathit{FF3}}} + \beta_P^MR_{M,t}^e+\beta_P^{\mathit{SMB}}{\mathit{SMB}}_t+\beta_P^{\mathit{HML}}{\mathit{HML}}_t+\varepsilon_{P,t} \label{eq:FF3a} \tag{6.4} \end{align} \]

• これに基づいて推定されたFF3アルファ\(\hat{\alpha}_P^{\mathit{FF3}}\)は，そのポートフォリオの超過リターンが，FF3モデルが予測するパフォーマンスから平均的にどの程度正負に乖離しているかを意味する．したがって，FF3モデルがポートフォリオの超過リターンをうまく説明する限り，\(\hat{\alpha}_P^{\mathit{FF3}}\)はゼロになるはずである．

---

3.5 目標を実現するためのコード

Code

# 推定結果を保存するために空のリストを準備
FF3_results <- list(NA)  

# ポートフォリオごとにFF3アルファの推定

for(i in 1:10) {
  FF3_results[[i]] <- ME_sorted_portfolio %>% 
    filter(ME_rank10 == i) %>%
    lm(Re ~ R_Me + SMB + HML, data = .) %>% # 3ファクターの実現値を独立変数として重回帰
    tidy() %>% 
    mutate(ME_rank10 = as.factor(i)) %>% # 推定対象のポートフォリオ名を保存
    select(ME_rank10, everything()) # ME_rank10を第一列に移動
}

# 複数のデータフレームから構成されるリストを一つのデータフレームに統合
binded_FF3_results <- bind_rows(FF3_results) 

---

3.6 FF3アルファの可視化

• 先のスライドでCAPM_alphaを図示した要領で，ポートフォリオごとにFF3アルファを描画してみよう．
• 次スライドのコードでは，binded_FF3_resultsから各ポートフォリオの定数項\(\hat{\alpha}_P^{\mathit{FF3}}\)を抽出した後，それを棒グラフで可視化している．

Code

binded_FF3_results %>% 
  filter(term == "(Intercept)") %>% # 定数項に関する推定結果のみを抽出
  ggplot() +
  geom_col(aes(x = ME_rank10, y = estimate)) + # 横軸をME_rank10，縦軸をFF3_alphaとする棒グラフ
  geom_hline(yintercept = 0) + 
  labs(x = "ME Rank", y = "FF3 alpha") + 
  scale_y_continuous(limits = c(-0.003, 0.013)) +
  theme_classic()

---

3.7 結果の解釈

• 出力されたFF3_alphaのグラフを見てみると，いずれのポートフォリオもアルファにほとんど差がないことが分かる．
• この結果はCAPM_alphaのそれと対照的であり，CAPMが説明できなかった平均超過リターンの違いを，FF3モデルではうまく説明できることが分かる．
• 定義上，線形ファクター・モデルは任意の銘柄やポートフォリオのリスクプレミアムを説明するはずである．したがって，ファクター調整済みのアルファが規則性を持って観察されるということは，そのファクター・モデルが現実には成立していない証拠となる．
• 規模別ソートという簡単な手順でアルファが観察される以上，CAPMは実証的な説明力が高いとは言い難い．それとは対照的に，FF3モデルは必要最小限のファクター数で，規模別ソートを含む様々な種類のポートフォリオのリターンを説明できるという意味で支持を集めてきたのである．

Footnotes

1. 一般に，投資対象となる資産のことを投資ユニバースと呼ぶ．