準備
パッケージ
Code
#パッケージの読み込み
rm(list=ls()); gc(); gc();
if (!require("pacman")) install.packages("pacman")
pacman::p_load(tidyverse, magrittr, summarytools, showtext, here, kableExtra)
#font_add_google("Noto Sans JP", "jp")
- 1
-
前の作業など,rのメモリに入っているものをリセットするコマンド
- 2
-
パッケージ管理用のパッケージである
pacmanが入っていない場合はインストール
- 3
-
複数のパッケージを一度に呼び出す
- 4
-
日本語で図表を作ったときに文字化けするのを防ぐための処理
データ
Manabaのコンテンツ(教材)→データ→第4回にあるデータファイル(csvファイル)をダウンロードしてデスクトップに置いてください。
データを要約する
データ解析の出発点は,データを効率的に整理・要約することで,その特徴を抽出すること
これを記述統計学と呼ぶ(↔︎️推測統計学)
データを確認する方法
データを集計した結果,例えば
Code
学番 <- c(1 : 10)
数学 <- c(100, 98, 70, 90, 60, 10, 50, 70, 90, 100)
英語 <- c(60, 90, 90, 80, 80, 80, 60, 60, 50, 100)
国語 <- c(50, 40, 30, 60, 50, 40, 30, 70, 80, 30)
exams <- tibble(学番, 数学, 英語, 国語)
exams
このままでは,全体としてどんな特徴があるのかがわかりません。
膨大なデータの特徴を捉えるためには,代表的な値を使うといいです。
ここからは基本的に比例尺度を想定して
\(X_i = X_1, X_2,...X_n\) とします。
平均値
データに含まれる値をすべて足してデータの数で割った値。\(\bar X\) とすると。
\[ \bar X = \frac{\text{データの総和}}{\text{データの数}}= \frac{X_1 + X_2 + ... X_n }{n} = \frac{1}{n} \sum_{i=1}^{n} X_i \]
平均値は統計的推測に際して重要な性質を持っていますが,データの重心を表すもので,必ずしもデータの真ん中を表しているわけではないことに注意が必要です。
Code
data3_1 <- c(100, 90, 80, 70, 60, 40, 10)
mean(data3_1)
- 1
-
データを作成して,
data3_1という名前で保存
- 2
-
mean()で,平均値を計算
Code
#これは以下でも同じ
sum(data3_1) / length(data3_1)
- 1
-
sum() は()内で指定したデータを合計する関数,length() はデータの数(行数)を吐き出す関数。data3_1は7行なので7が吐き出される。
中央値
データを順番に並べてちょうど真ん中の値。メディアン(median)とも
平均に比べて極端な値の影響を受けにくいという特徴があります。
- 年収や貯蓄額のような少数の大金持ちが含まれるデータでは,平均よりも中央値のほうが実感に近いことも
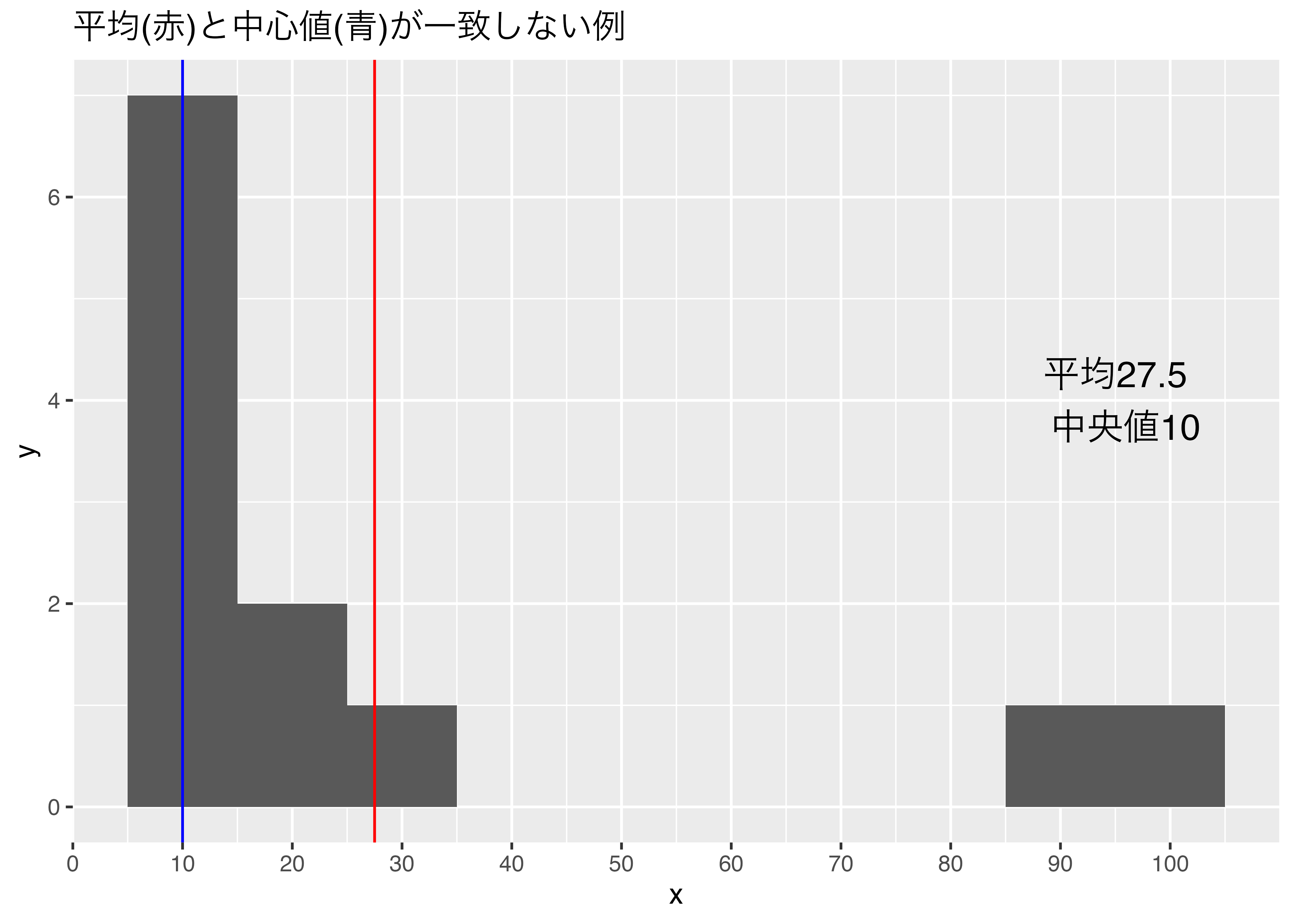
平均値と中央値はそれぞれデータの代表的な値ではありますが,必ずしも一致しません。例えば以下のようなデータがあったとします。
Code
x <- c(10, 10, 10, 10, 10, 10, 10, 20, 20, 30, 90, 100)
平均と中央値はそれぞれ違います。
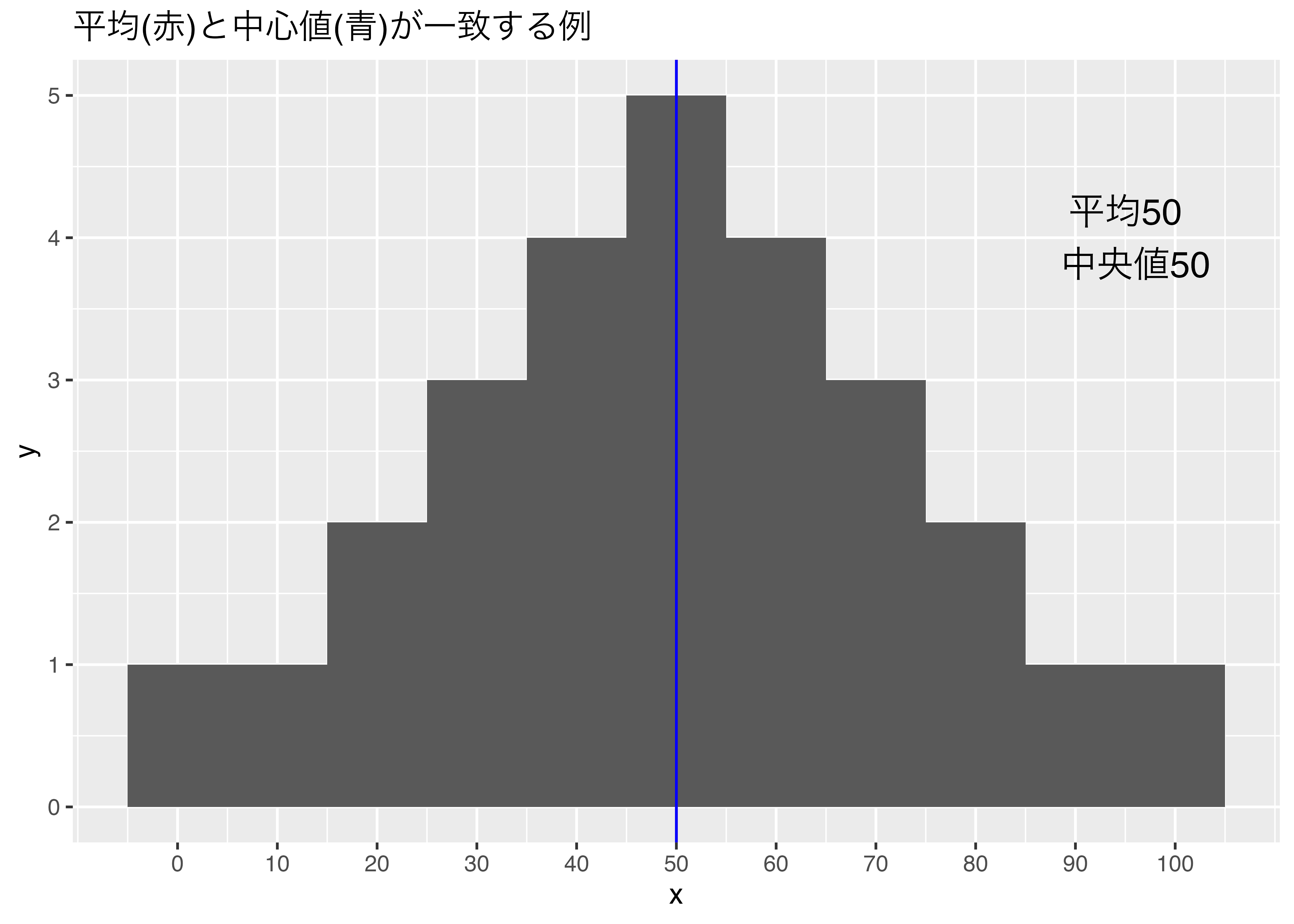
一致する場合もあります。
分散
データのばらつき度合いを表します。例えば,A, Bという2つのクラスがあるとします。ある教科のテストの平均,中央値が両クラスとも60だったとしても,
Code
data3_2a <- c(20, 60, 100, 30, 90)
data3_2b <- c(60, 60, 60, 60, 60)
というように得点の分布が全く異なる場合があり得ます。この違いは平均や中央値だけでは読み取れません。この違いを表す,平均からのばらつき度合いを把握する指標が分散です。
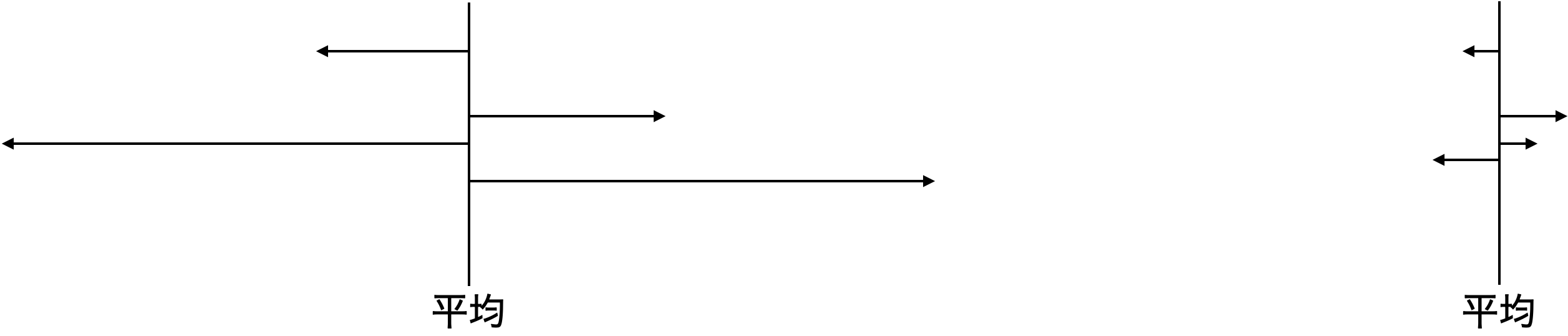
平均からの距離 (\(\bar X - X_i\))は,プラスにもマイナスにもなり,足し合わせたら0になってしまうので,これを2乗した\((\bar X - X_i)^2\)をデータの数だけ足し合わせて,データの数で割ったものを分散とします。
\[
Var(X) = \frac{1}{n} \sum_{i = 1}^n(\bar X - X_i)^2
\]
分散は大きければ大きいほどばらつき度合いが高いということを意味します。
Code
meana <- mean(data3_2a)
sa <- meana - data3_2a
sua <- sum(sa^2)
分散a <- sua / length(data3_2a)
分散b <- sum((mean(data3_2b) - data3_2b)^2) / length(data3_2b)
- 1
-
こんなふうに変数名は日本語でも大丈夫ですが,全角半角の切り替えが面倒くさかったり,ミスの元なのであまりやらない方がいいと思います。
Aの分散は1000,Bの分散は0。
標準偏差
分散の数値は何を意味しているのかがわからないです。なぜなら,元の点数(100点満点)を2乗しているからです。これをルートを取って元に戻すと,元の数値や平均値と同じ単位になります。分散のルートを取ったものを標準偏差といいます。
\[
SD(X) = \sqrt{\text{分散}} = \sqrt{\frac{1}{n} \sum_{i = 1}^n(\bar X - X_i)^2}
\]
まとめ
| 平均 |
データの重心 |
\(\bar X = \frac{1}{n} \Sigma_{i=1}^{n} X_i\) |
| 中央値 |
データを大きさ順に並べたときの真ん中 |
省略 |
| 最小値 |
データの中で最も小さい値 |
|
| 最大値 |
データの中で最も大きな値 |
|
| 分散 |
データのばらつき度合い |
\(Var(X) = \frac{1}{n} \Sigma_{i = 1}^n(\bar X - X_i)^2\) |
| 標準偏差 |
分散の平方根 |
\(SD(X) = \sqrt{\text{分散}} = \sqrt{\frac{1}{n} \Sigma_{i = 1}^n(\bar X - X_i)^2}\) |
偏差値
日本の受験で多く使われる学力偏差値は以下のように算出されます。
\[
\text{偏差値} = {10\frac{(X_i-\bar X)}{SD}}+50
\]
自分の点数と平均値の差を標準偏差で割ったものに10をかけて,50を足す。
こうすることで,平均点のとき偏差値50(\((X_i-\bar X)=0\))となり,標準偏差1つ分の差が偏差値10の差になるように調整されています。
あとで出てくる確率分布(正規分布)の性質から,それぞれの偏差値から自分の相対的位置が推定できるようになります。
データの可視化
グラフを使ったデータの要約
- 名義尺度など,計算が不可能なものを要約し,可視化する方法として,度数分布表や棒グラフ,円グラフ等があります
- また,定量的な尺度を可視化する方法として,ヒストグラムや箱ひげ図などが多く使われます。
これらはいずれもデータの概要を視覚的に表現するものです。
- 一方で,データの可視化はその見せ方によって人の印象を操作することができてしまいます。
- グラフを書くことは,分析でもなんでもないと言うことには注意が必要です。
度数分布表と棒グラフ
- 度数分布表
-
名義尺度や順序尺度(もしくは範囲を区切った量的変数)ごとにどれほどデータがあるかをまとめた表
ここでは,例としてある2クラスのメンバーそれぞれのクラス(class),性別(gender),テストの点(test),出身地(hometown)が含まれたdata3.csvを使います
Code
data3 <- here("data","3_test.csv") |> read_csv()
data3
出身地の度数分布表を作ってみます。最も簡単な方法は,hometownについてtable()コマンドを使って
Code
京都 兵庫 北海道 大阪 奈良 島根 滋賀
7 6 1 10 3 1 2
出身地別に何人いるかがわかります。
もう少し見栄えの良いものは,summarytoolsパッケージのfreq()コマンドでできます。
Code
freq(data3$hometown,
report.nas = FALSE,
display.labels = FALSE,
display.type = FALSE,
headings = FALSE,
style = "rmarkdown")
| 京都 |
7 |
23.33 |
23.33 |
| 兵庫 |
6 |
20.00 |
43.33 |
| 北海道 |
1 |
3.33 |
46.67 |
| 大阪 |
10 |
33.33 |
80.00 |
| 奈良 |
3 |
10.00 |
90.00 |
| 島根 |
1 |
3.33 |
93.33 |
| 滋賀 |
2 |
6.67 |
100.00 |
| Total |
30 |
100.00 |
100.00 |
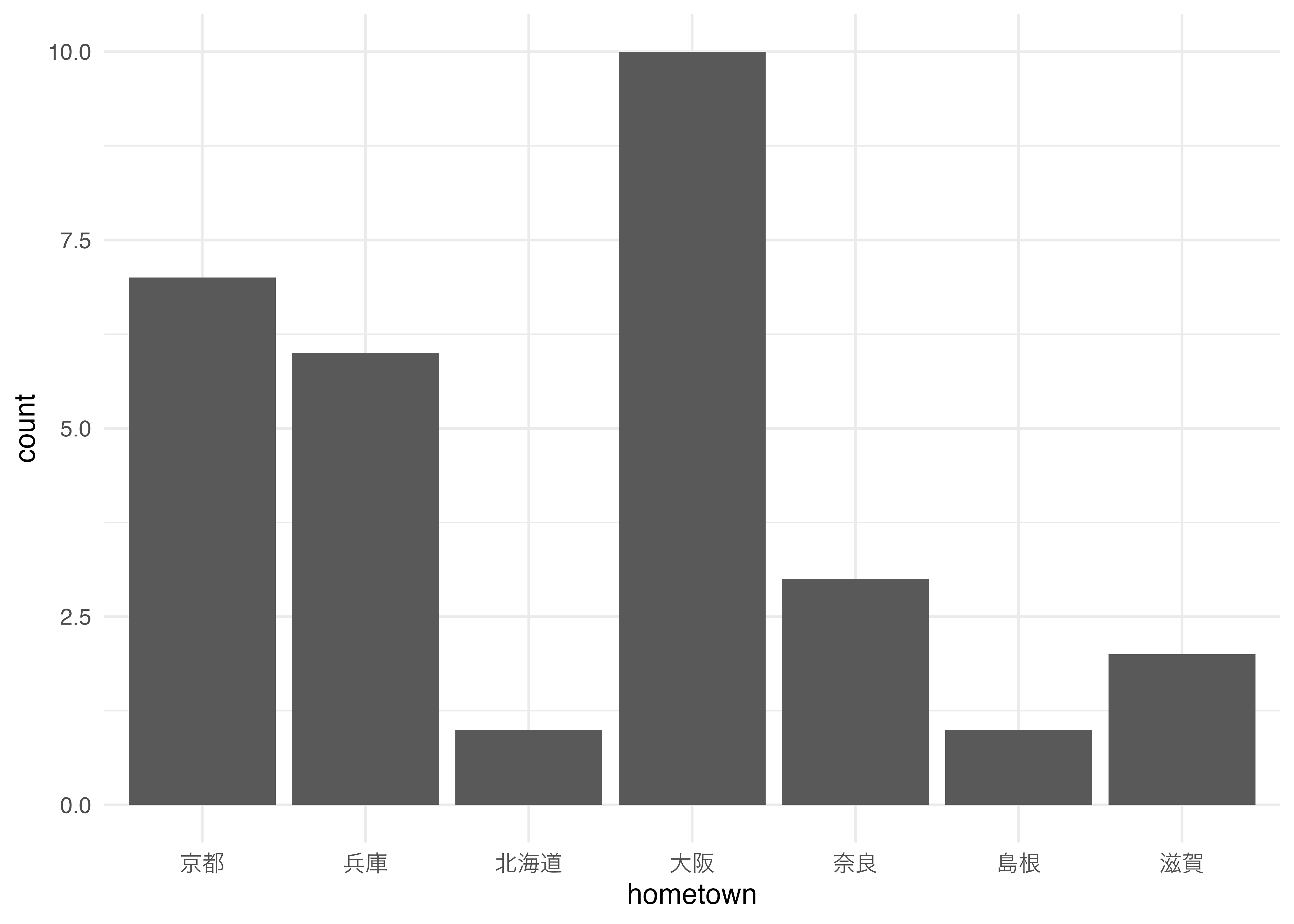
棒グラフ
カテゴリごとの度数を棒の高さで表したら棒グラフになります。
Code
data3 |>
ggplot(aes(x = hometown)) +
geom_bar() +
theme_minimal()
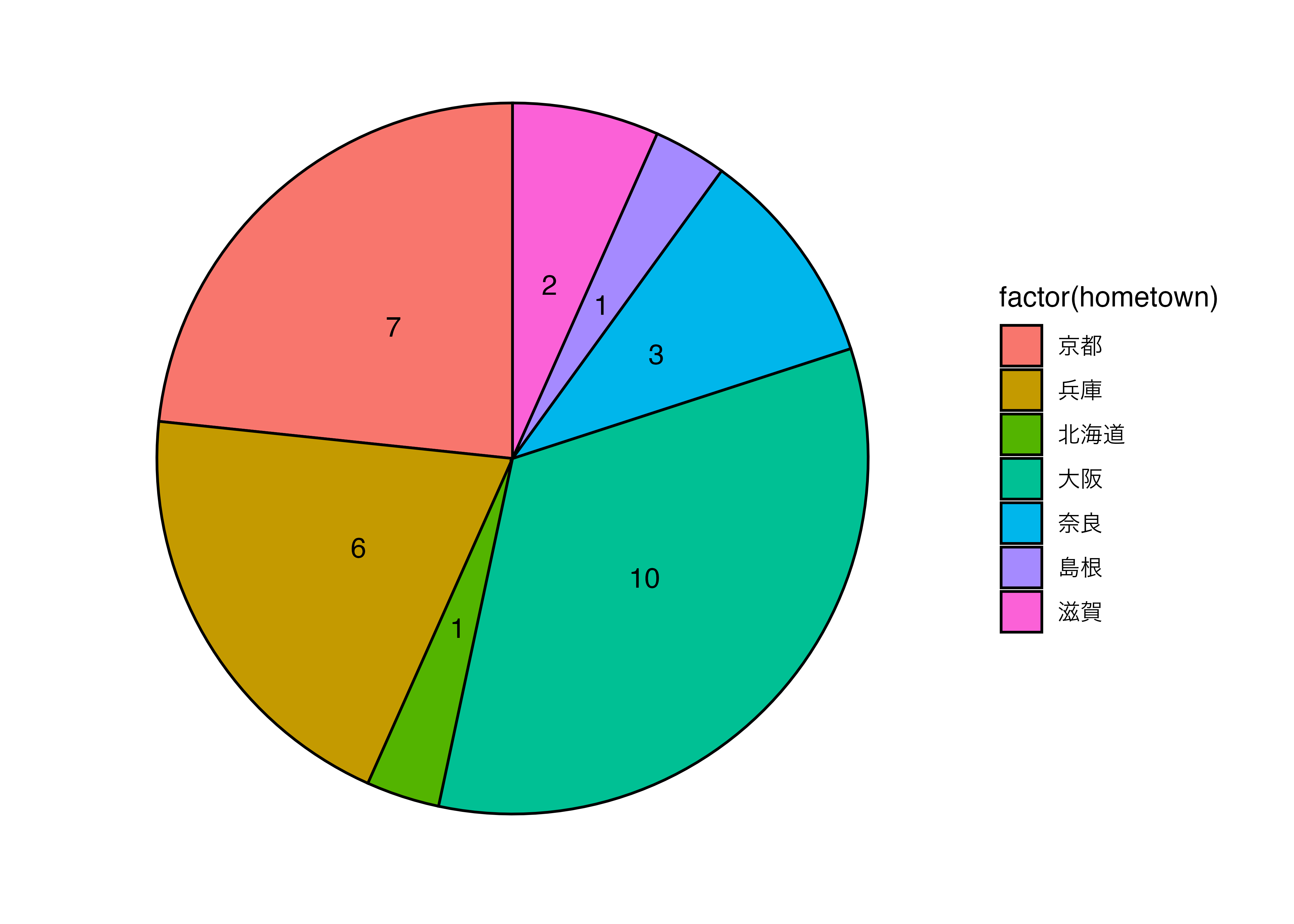
割合を見やすくするなら円グラフ
- 全体が100%になるので,ある値の全体の中での割合が見えやすくなります。
Code
data3 |>
ggplot(aes(x = 1, fill = factor(hometown))) +
geom_bar(stat = "count", color = "black")+
coord_polar(theta = "y")+
theme_minimal(base_family = "Sans") +
theme(panel.grid = element_blank(),
axis.title = element_blank(),
axis.text = element_blank(),
axis.ticks = element_blank()) +
geom_text(stat = "count",
aes(x = 1, y = after_stat(count),
label = after_stat(count)),
position = position_stack(vjust = 0.5))
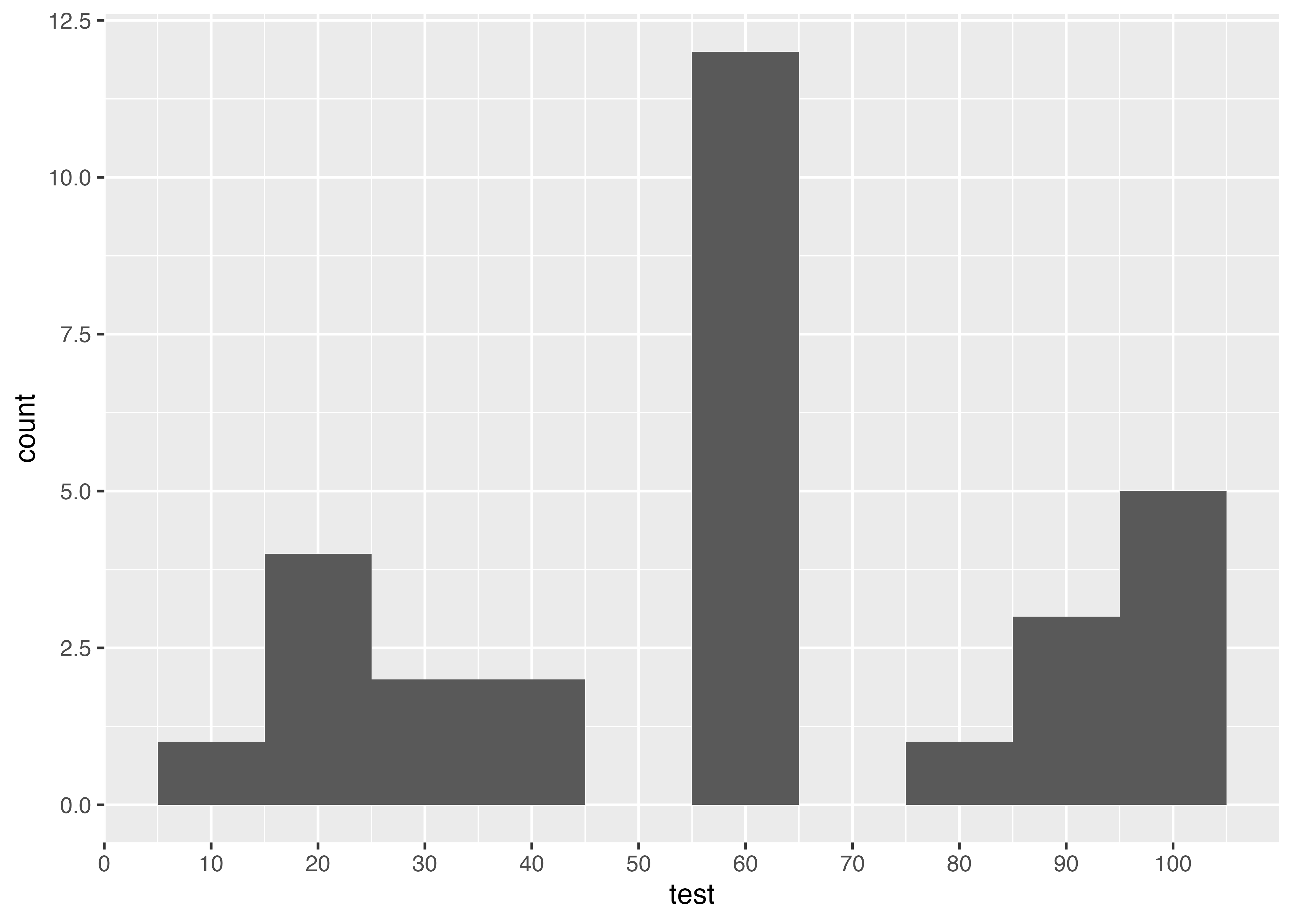
ヒストグラム
特定のカテゴリごとの度数がわかるグラフです。例えばテストの点数なら,特定の範囲にどれぐらいの人がいるかがわかります。棒グラフとは違って,連続的な変数をある一定の範囲で区切っています。
Code
data3 |>
ggplot(aes(test)) +
geom_histogram(breaks = seq(5, 105, 10)) +
scale_x_continuous(breaks = seq(0, 100, 10))
- 1
-
x軸の基準を指定
- 2
-
ヒストグラムを作成(10点刻み)
- 3
-
ラベルを作成(10点刻み)
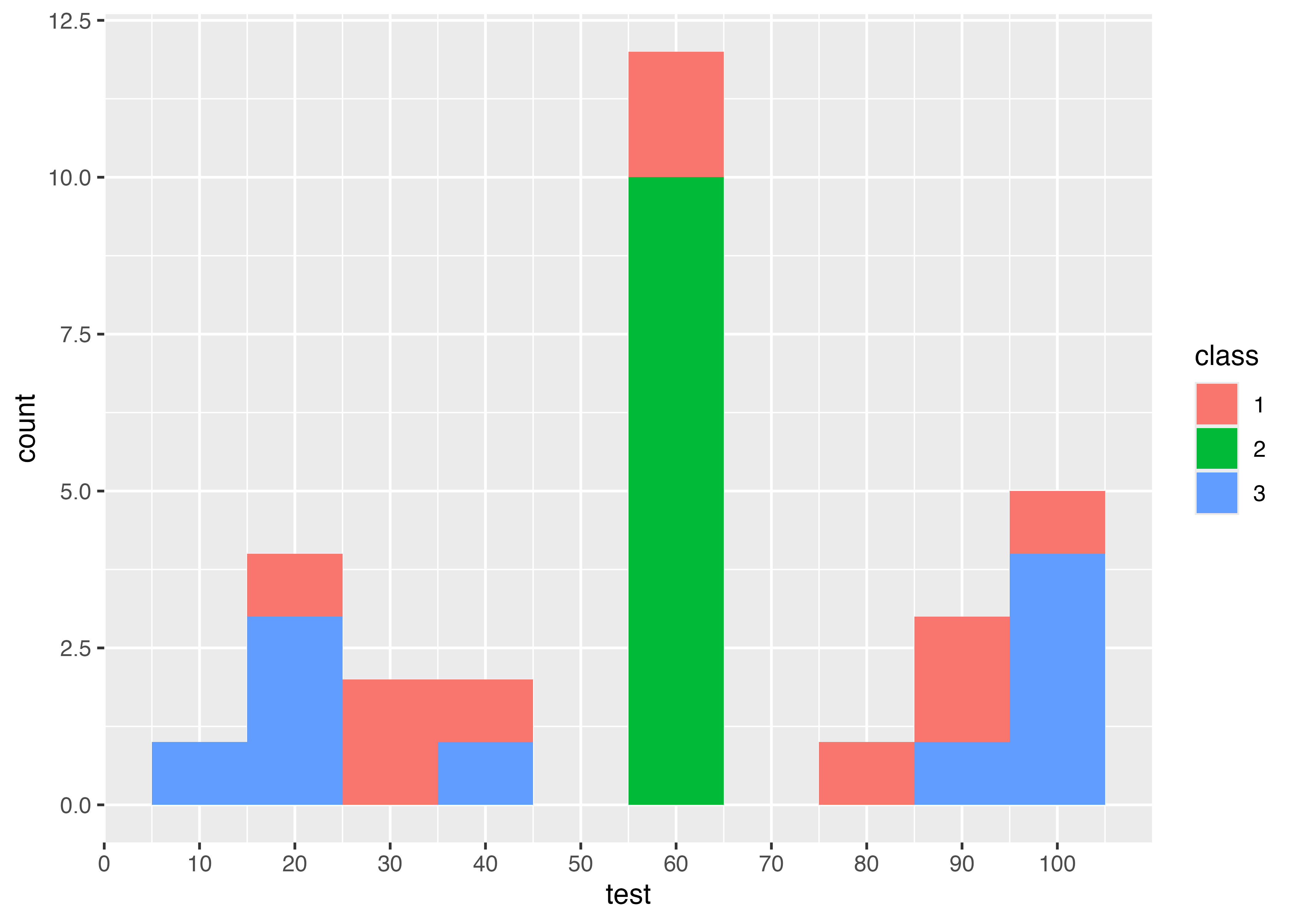
例えば,グループごとに色分けする
Code
data3 <- data3 |>
mutate(class = as.factor(class))
data3 |>
ggplot(aes(test, fill = class)) +
geom_histogram(breaks = seq(5, 105, 10)) +
scale_x_continuous(breaks = seq(0, 100, 10))
クラスごとに分けて作成
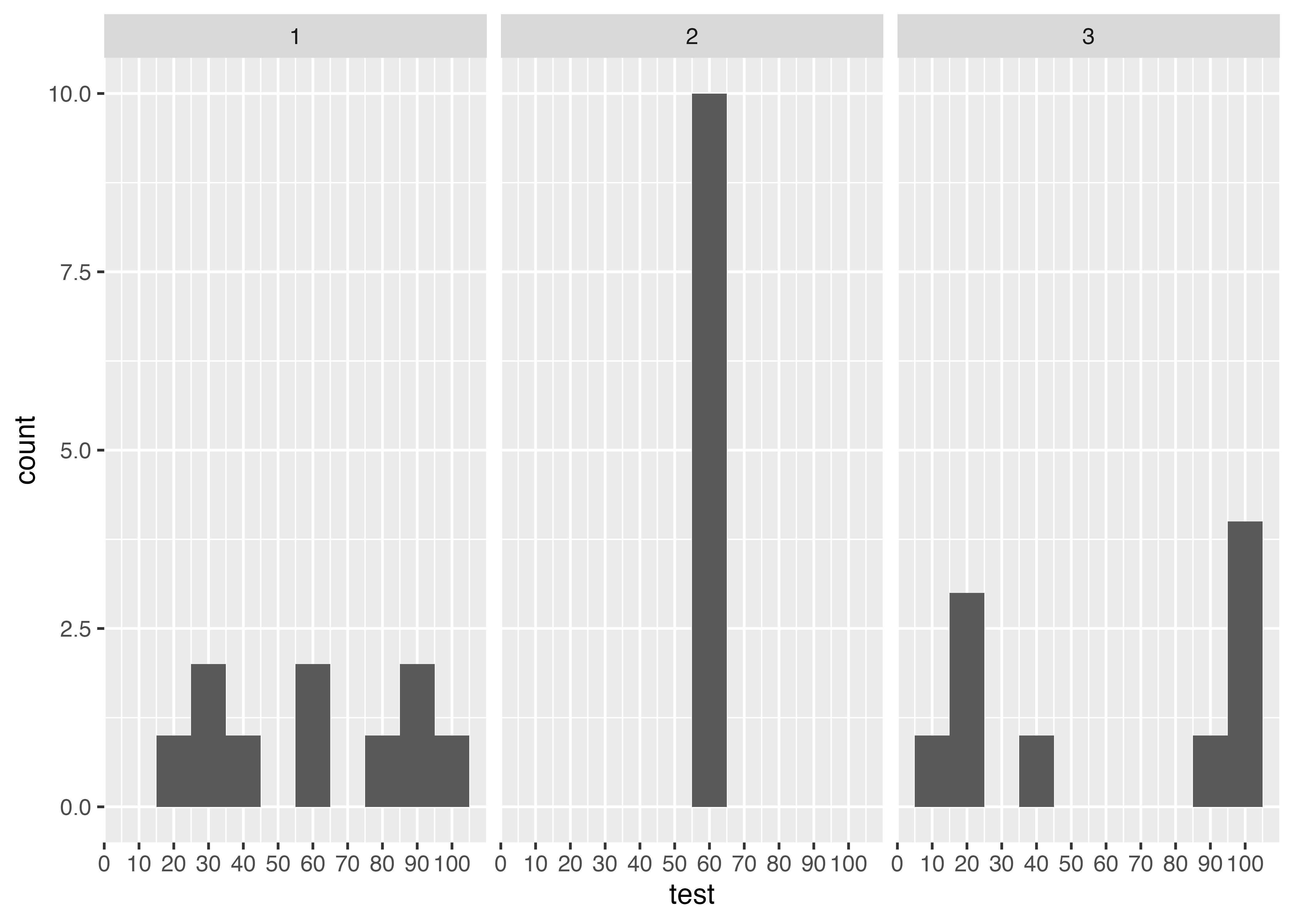
Code
data3 %>%
ggplot(., aes(test)) +
geom_histogram(breaks = seq(5, 105, 10)) +
scale_x_continuous(breaks = seq(0, 100, 10)) +
facet_grid(~class)
これだと,平均がどれも60点の3クラスだけど,得点のばらつき度合いが大きく違う,ということがわかりやすいです。
箱ひげ図
複数のグループごとの中央値やばらつき度合いを視覚的に表現できます。ここでは,クラスごとのテストの点数の箱ひげ図を書きます。
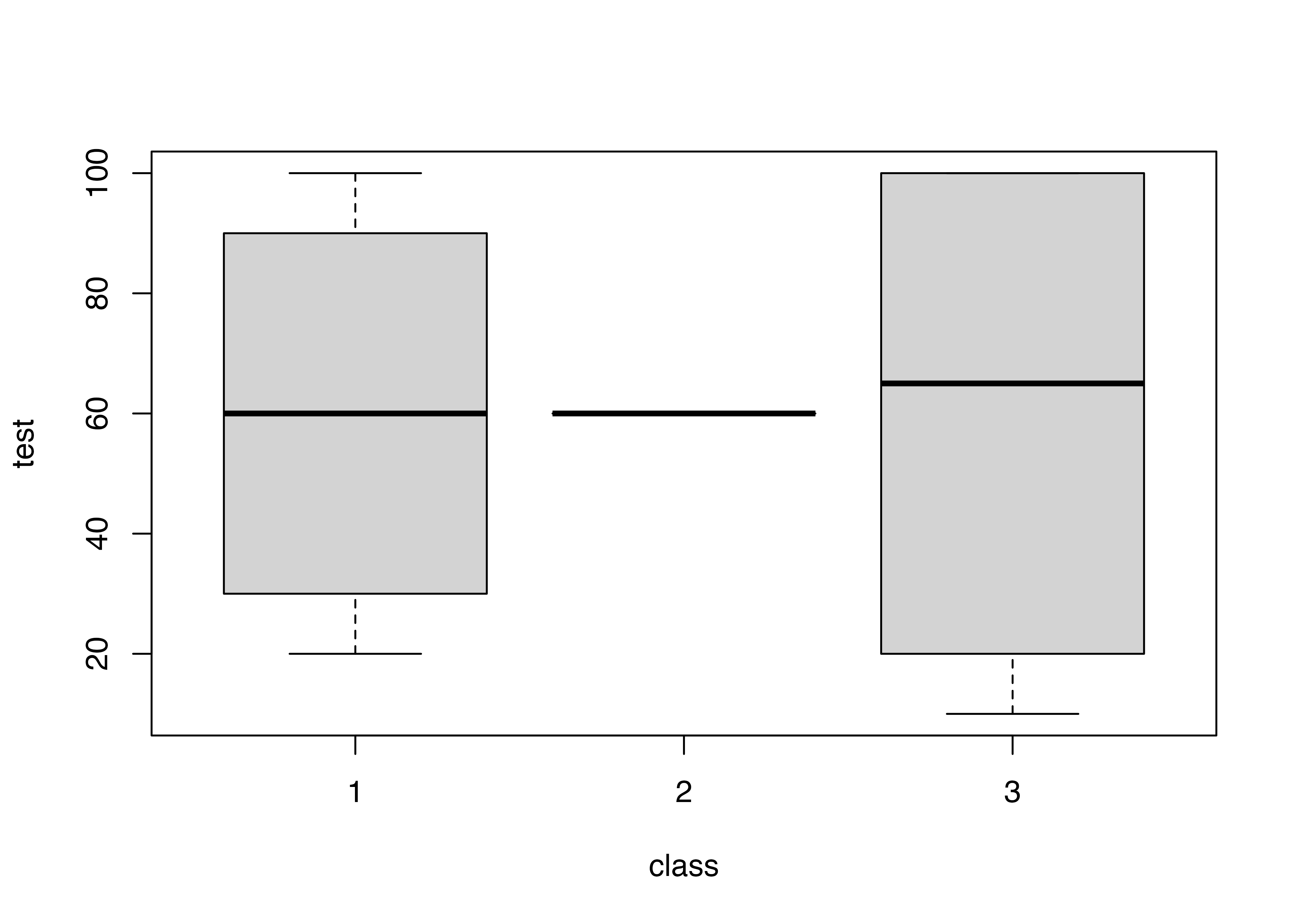
Code
boxplot(test ~ class, data = data3)
- 1
-
boxplot()で箱ひげ図が書ける。()の中は(表示したい数値 ~ 場合分けしたいカテゴリ変数)
- 最も外の線は最大値と最小値,箱の上下はそれぞれ75%点と25%点,つまり上下4分の1の点,真ん中の太線は中央値です。
- クラス2は全員が60点だったので,箱がなく中央値の線だけが記載されています(箱が潰れて線になっているイメージ)
男女別に分ける
Code
boxplot(test ~ gender, data = data3)
参考: 表示方法と詐欺グラフ
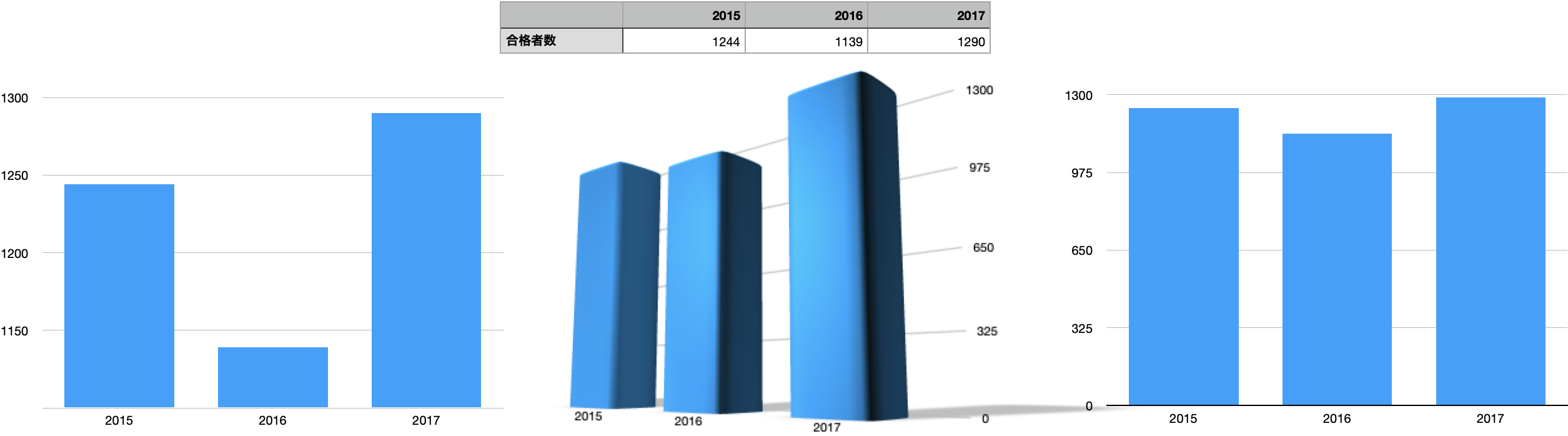
これらは全部同じデータから作った棒グラフです
リンクは,実態を歪んでみせるような可視化方法,いわゆる詐欺グラフを集めたnoteです。悪い例がたくさん載っています。表示の仕方で事実の受け取り方を操作しようという悪質な試みです。特に注意する点は,
- 3Dの棒グラフ・円グラフはやめよう
- メモリの間隔は統一しよう
- 0から始まらない棒グラフはやめよう
グラフはあくまでデータや分析結果の理解を補助するもの。グラフ書くだけ,は分析でもなんでもない