rm(list=ls()); gc(); gc();
if (!require("pacman")) install.packages("pacman")
pacman::p_load(magrittr,
estimatr, car, modelsummary,
ggrepel, patchwork, broom,
psych, ppcor, qgraph, AER,
datarium, tidyverse,
conflicted)
conflict_prefer("select", "dplyr")
conflict_prefer("filter", "dplyr")pacmanパッケージが入っていない場合は，インストールする
主要なパッケージ
pacman複数のパッケージを読み込めるパッケージ。そのパッケージの中のp_loadコマンドを使うと，（）内に指示したパッケージを読み込める。さらにそのパッケージがそもそもインストールされていない場合にはインストールした後に読み込んでくれる
tidyverseRのコードを楽にするたくさんのパッケージをパッケージにしたもの
magrittrtidyverseに含まれる%>%などのコードをさらに拡張するもの。これがあると%$%とか%<>%が使える
前回と同じデータで分析を続けます。kadai_8.csvには，ある大学の授業における学生19名の入学試験結果 (exam,700点満点)，入学から現在までのGPA (gpa)，高校の時の評定平均 (hschool, 10段階)が含まれています。ここから，GPAが入学時点で得られる情報とどのような関係にあるかを検証したいと考えています。
hschool)の中央値を求めてください（コードと結果）test <- read_csv("data/9_kadai.csv")
median(test$hschool)[1] 7.3medhs <- median(test$hschool)hschool)が中央値よりも高い時に1を取るダミー変数(名前はhsdummyとして)を作成してください（コード）test %<>%
mutate(hsdummy = 1 * (medhs <= hschool))hschoolの代わりに2で作ったダミー変数と入試結果(exam)を独立変数，従属変数を大学GPA（gpa）とした回帰分析をしてください。（コードと結果の解釈）lm(gpa ~ exam + hsdummy, data = test) |>
summary()
Call:
lm(formula = gpa ~ exam + hsdummy, data = test)
Residuals:
Min 1Q Median 3Q Max
-0.70307 -0.35548 0.07641 0.30470 0.78999
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.587025 0.935470 -1.697 0.109156
exam 0.007457 0.001820 4.097 0.000842 ***
hsdummy 0.220000 0.255156 0.862 0.401307
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5115 on 16 degrees of freedom
Multiple R-squared: 0.599, Adjusted R-squared: 0.5488
F-statistic: 11.95 on 2 and 16 DF, p-value: 0.000669examの係数が正で統計的に有意(p < 0.001)。テストが1点上がると，gpaが0.007上がる。hsdummyは有意ではない。
gpaを従属変数として，2で作った変数とexamの交互作用を含めた回帰分析をしてください（コードと結果の解釈）lm(gpa ~ exam*hsdummy,data = test) |>
summary()
Call:
lm(formula = gpa ~ exam * hsdummy, data = test)
Residuals:
Min 1Q Median 3Q Max
-0.69884 -0.35740 0.08176 0.30868 0.79301
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.6342050 1.3372311 -1.222 0.2405
exam 0.0075501 0.0026232 2.878 0.0115 *
hsdummy 0.3223502 2.0230608 0.159 0.8755
exam:hsdummy -0.0001919 0.0037608 -0.051 0.9600
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5283 on 15 degrees of freedom
Multiple R-squared: 0.599, Adjusted R-squared: 0.5188
F-statistic: 7.47 on 3 and 15 DF, p-value: 0.002748交互作用は有意ではない
examを対数変換した変数(lexam)とgpaを対数変換したlgpaを下記のコードを用いて作ってください。その上で，lgpaを従属変数，独立変数をlexam，hschoolとして回帰分析をしてください（コードと結果の解釈）test %<>%
mutate(lexam = log(exam),
lgpa = log(gpa))lm(lgpa ~ lexam + hschool, data = test) |>
summary()
Call:
lm(formula = lgpa ~ lexam + hschool, data = test)
Residuals:
Min 1Q Median 3Q Max
-0.41222 -0.11330 0.00259 0.13319 0.38106
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -9.14274 3.10253 -2.947 0.00947 **
lexam 1.51185 0.55213 2.738 0.01458 *
hschool 0.07572 0.07899 0.959 0.35202
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2215 on 16 degrees of freedom
Multiple R-squared: 0.5938, Adjusted R-squared: 0.543
F-statistic: 11.7 on 2 and 16 DF, p-value: 0.0007411lexamはlgpaと正の関係にあり，5%水準で有意(p < 0.05)。試験の点数が1％高いと，gpaが1.51%高くなる。
xがyの原因となる
「国民健康・栄養調査」による年齢別の身長・体重データ
height_weight <- read_csv("data/12_height_weight.csv")
height_weight |>
ggplot(aes(x = Weight_m, y = Height_m)) +
geom_point()
lm(Height_m ~ Weight_m, data = height_weight) |>
summary()
Call:
lm(formula = Height_m ~ Weight_m, data = height_weight)
Residuals:
Min 1Q Median 3Q Max
-19.024 -6.791 1.333 6.576 12.108
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 84.79730 2.43480 34.83 <2e-16 ***
Weight_m 1.33911 0.04636 28.89 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.615 on 60 degrees of freedom
Multiple R-squared: 0.9329, Adjusted R-squared: 0.9318
F-statistic: 834.5 on 1 and 60 DF, p-value: < 2.2e-16身長と体重は有意に正の関係がある。
でも，これは明らかに因果関係ではない。
おそらく単なる相関関係
偶然相関があるように見える
人口あたりのチーズの消費量とベッドシーツに絡まって死ぬ人の数
アメリカの科学・宇宙・テクノロジーに対する支出と首吊り，絞殺，窒息による自殺者数
つまり…
単に相関を計算したり，回帰分析をしただけではx → yという因果関係はわからない。
因果関係を推論することは結構難しい。
仮に薬の効果を知りたいとしたら，薬を投与した人と投与しない人1人ずつのその効果（例えば血液検査の結果数値など）を比べる？
適切な比較はできない
本来的には薬の効果（薬と症状改善の因果関係）は「同じ人が投与した場合と投与していない場合」を比較しないといけない。
でも，現実に観察されるのはどっちか。薬ありもしくは薬なしどっちかのデータしか取れない。
パラレルワールド・タイムマシンがない限り実現できない。反実仮想が必要。因果推論の根本問題とか言われる
たくさんの参加者を集めて，その人たちにランダムに処置（投与するかしないか）を割り振る
ランダムに割り振った集団間の比較をすることで薬の「平均的な」効果を推定することができる
個人レベルで見ると因果関係はそもそも検証が不可能
集団レベルでランダムに処置を割り振ることで，平均的な効果の推定を通した因果関係が可能
このことを使って
(星野, 田中, and 北川 2023 , CRESCO Tech Blog)
# 平均値、分散を指定していい感じに作る
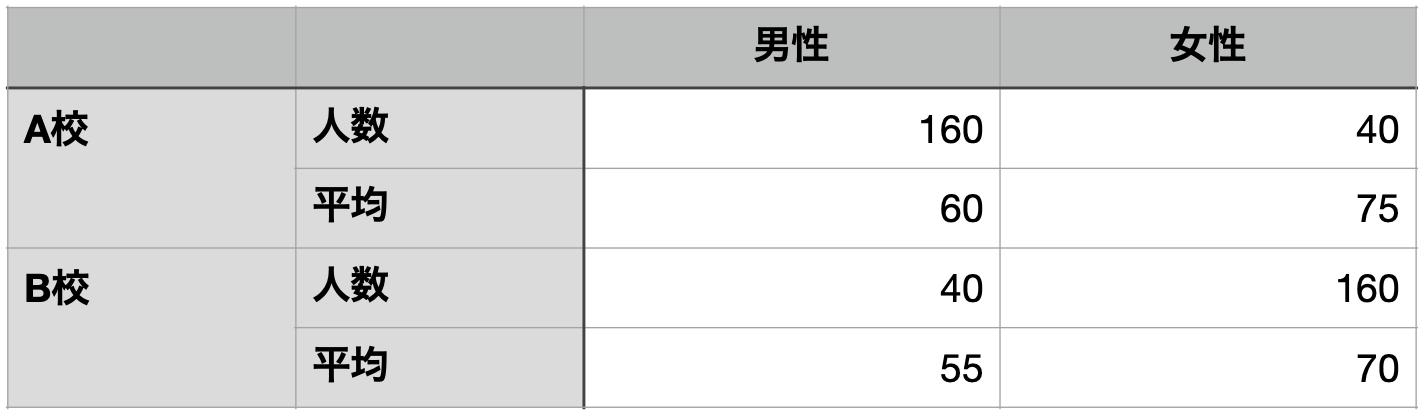
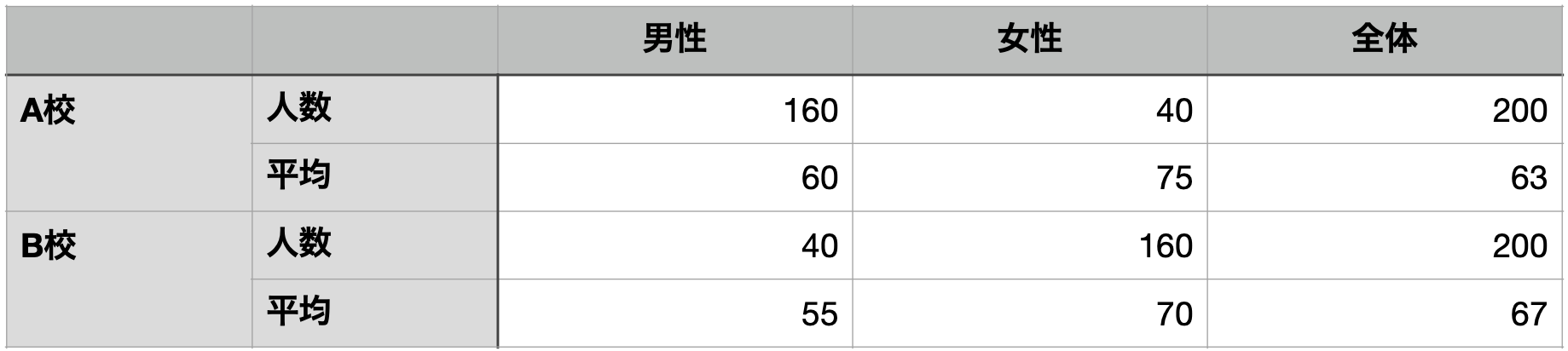
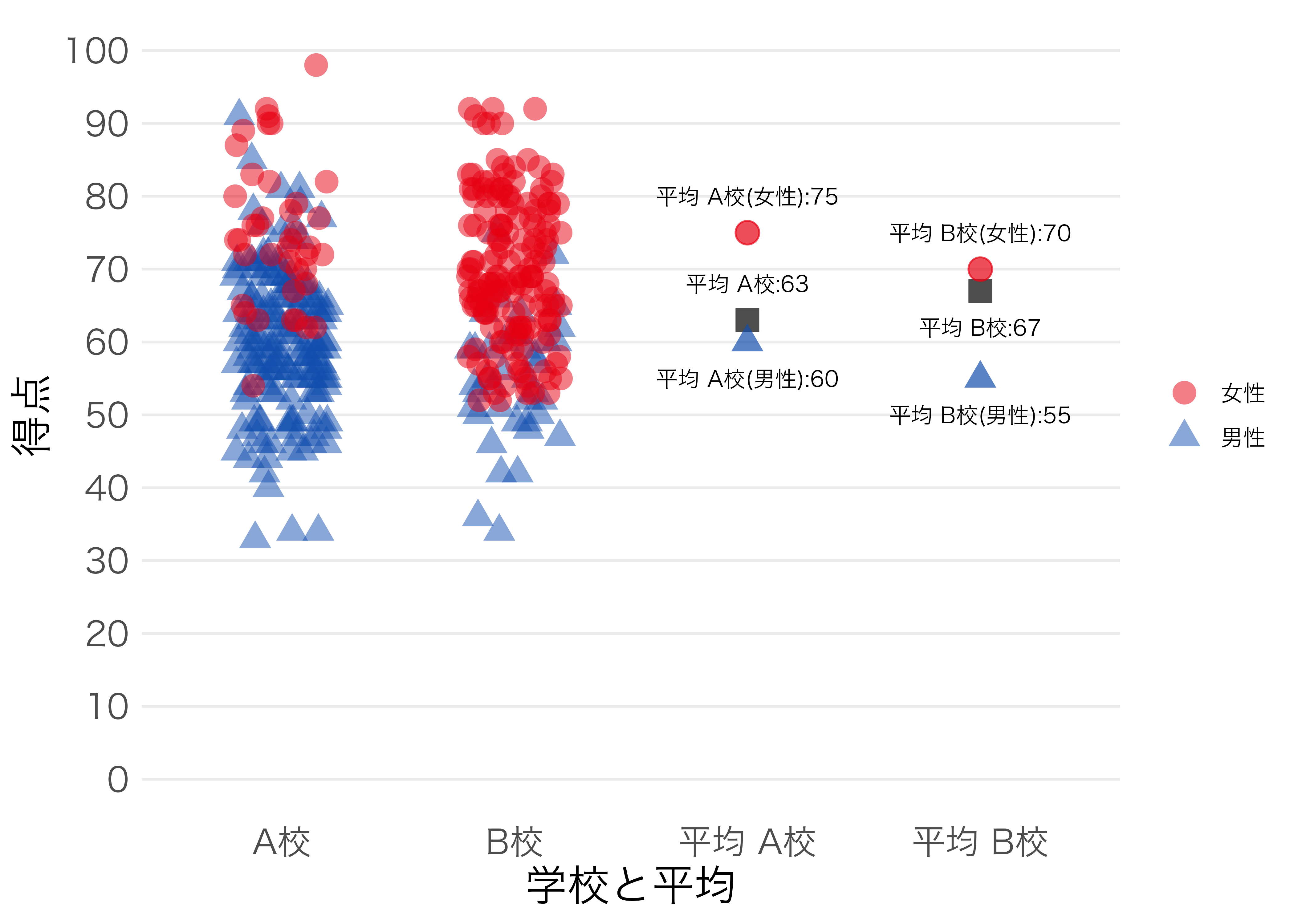
a_male <- round(rnorm(n = 160, mean = 60, sd = 10), 0)
a_female <- round(rnorm(n = 40, mean = 75, sd = 10), 0)
b_male <- round(rnorm(n = 40, mean = 55, sd = 10), 0)
b_female <- round(rnorm(n = 160, mean = 70, sd = 10), 0)
# その後、四捨五入しているので結局、微調整を手でしています。
a_male <- c(
45, 63, 55, 68, 60, 66, 64, 71, 46, 56,
71, 60, 42, 46, 53, 68, 72, 56, 64, 46,
47, 66, 65, 55, 55, 49, 66, 60, 44, 64,
60, 60, 34, 66, 63, 58, 62, 45, 66, 66,
60, 64, 53, 58, 69, 59, 65, 55, 58, 57,
76, 56, 67, 56, 76, 34, 53, 67, 49, 63,
59, 44, 53, 63, 48, 59, 60, 66, 53, 58,
40, 49, 56, 63, 57, 55, 74, 58, 61, 68,
74, 63, 64, 68, 77, 49, 69, 69, 63, 56,
67, 54, 49, 79, 60, 62, 63, 71, 71, 57,
56, 70, 81, 81, 58, 57, 54, 69, 64, 70,
56, 62, 66, 85, 63, 75, 59, 68, 65, 57,
59, 69, 91, 78, 59, 60, 55, 48, 52, 55,
52, 57, 70, 70, 58, 45, 49, 61, 46, 64,
50, 57, 71, 65, 47, 69, 59, 72, 49, 54,
71, 33, 61, 66, 53, 49, 47, 61, 57, 48)
a_female <- c(
80, 73, 92, 98, 75, 72, 65, 72, 62, 63,
83, 90, 82, 77, 79, 70, 73, 87, 72, 76,
70, 76, 82, 72, 67, 68, 71, 54, 78, 74,
90, 91, 74, 64, 63, 74, 77, 89, 63, 62)
b_male <- c(
56, 64, 61, 60, 53, 66, 65, 51, 50, 54,
50, 52, 51, 59, 59, 52, 61, 72, 42, 55,
42, 58, 49, 59, 60, 36, 75, 48, 34, 64,
53, 62, 46, 60, 47, 54, 59, 49, 55, 57)
b_female <- c(
90, 80, 62, 73, 60, 76, 75, 68, 82, 82,
67, 79, 71, 81, 54, 82, 65, 77, 71, 61,
62, 76, 71, 76, 62, 90, 55, 64, 83, 92,
66, 90, 71, 66, 80, 57, 63, 65, 71, 62,
55, 52, 68, 72, 79, 81, 76, 65, 65, 76,
75, 85, 74, 60, 59, 67, 63, 64, 81, 84,
81, 81, 55, 76, 80, 69, 84, 57, 78, 72,
63, 72, 82, 79, 58, 73, 52, 57, 58, 69,
73, 70, 83, 76, 58, 92, 65, 65, 65, 59,
80, 78, 68, 61, 64, 78, 62, 69, 81, 65,
91, 79, 68, 74, 68, 67, 81, 83, 67, 92,
67, 84, 75, 67, 67, 53, 62, 55, 68, 74,
65, 77, 75, 70, 68, 56, 74, 60, 65, 61,
54, 69, 68, 71, 67, 62, 66, 80, 69, 74,
69, 59, 69, 79, 69, 64, 67, 56, 66, 78,
85, 83, 53, 56, 56, 80, 53, 55, 70, 53)
# 表を作る関数
create_table <- \(male, female, school){
table_male <- tibble(male) |>
rename(得点 = male) |>
mutate(性別 = "男性")
table_female <- tibble(female) |>
rename(得点 = female) |>
mutate(性別 = "女性")
return(bind_rows(table_male, table_female) |>
mutate(学校 = school))
}
# A校とB校をユニオンする
data <- bind_rows(
create_table(a_male, a_female, "A校"),
create_table(b_male, b_female, "B校")
) |>
select(学校, 性別, 得点)
data %<>%
group_by(学校,性別) |>
mutate(平均点 = mean(得点)) 共通テストの結果をA校とB校，それぞれ男女別に集計した。男性，女性ともに成績が良いのはA校
ところが，全体を見ると
B予備校の方が高い…
これは，「シンプソンのパラドックス」として有名な現象
# プロパティとして使用する項目の関数
properties <- \() {
prop <- NULL
prop$add_mean_A_x <- "平均 A校"
prop$add_mean_A_y <- round(mean(data[data$学校 == "A校", ]$得点), 0)
prop$add_mean_B_x <- "平均 B校"
prop$add_mean_B_y <- round(mean(data[data$学校 == "B校", ]$得点), 0)
prop$add_mean_a_male_x <- "平均 A校"
prop$add_mean_a_male_y <- round(mean(data[data$学校 == "A校" &
data$性別 == "男性", ]$得点), 0)
prop$add_mean_b_male_x <- "平均 B校"
prop$add_mean_b_male_y <- round(mean(data[data$学校 == "B校" &
data$性別 == "男性", ]$得点), 0)
prop$add_mean_a_female_x <- "平均 A校"
prop$add_mean_a_female_y <- round(mean(data[data$学校 == "A校" &
data$性別 == "女性", ]$得点), 0)
prop$add_mean_b_female_x <- "平均 B校"
prop$add_mean_b_female_y <- round(mean(data[data$学校 == "B校" &
data$性別 == "女性", ]$得点), 0)
return(prop)
}
# ggplotで描画する関数
my_ggplot <- \(data, prop) {
g <- ggplot(
data = data,
mapping = aes(
x = data$学校,
y = data$得点)) + # ベースとなるデータの指定
geom_jitter(
size = 4,
alpha = 0.5,
height = 0,
width = 0.2,
mapping = aes(
shape = 性別,
colour = 性別
)
) + # 揺らぎを持たせたグラフ描画
scale_color_manual(values = c("#E60012", "#124DAE")) + # 配色指定
annotate(geom = "point",
x = prop$add_mean_A_x,
y = prop$add_mean_A_y,
size = 4, shape = 15, alpha = 0.7) + # A校の平均
annotate(geom = "point",
x = prop$add_mean_B_x,
y = prop$add_mean_B_y,
size = 4, shape = 15, alpha = 0.7) + # B校の平均
annotate(geom = "point",
x = prop$add_mean_a_male_x,
y = prop$add_mean_a_male_y,
size = 4, shape = 17, alpha = 0.7,
colour = "#124DAE") + # A校男性の平均
annotate(geom = "point",
x = prop$add_mean_b_male_x,
y = prop$add_mean_b_male_y,
size = 4, shape = 17, alpha = 0.7,
colour = "#124DAE") + # B校男性の平均
annotate(geom = "point",
x = prop$add_mean_a_female_x,
y = prop$add_mean_a_female_y,
size = 4, shape = 19, alpha = 0.7,
colour = "#E60012") + # A校女性の平均
annotate(geom = "point",
x = prop$add_mean_b_female_x,
y = prop$add_mean_b_female_y,
size = 4, shape = 19, alpha = 0.7,
colour = "#E60012") + # B校女性の平均
annotate(geom = "text",
family = "Hiragino Sans",
size = 3,
x = c("平均 A校", "平均 B校"),
y = c(prop$add_mean_A_y + 5,
prop$add_mean_B_y - 5),
label = c(paste0("平均 A校:",
prop$add_mean_A_y),
paste0("平均 B校:",
prop$add_mean_B_y))) + # A校の平均
annotate(geom = "text",
family = "Hiragino Sans",
size = 3,
x = c("平均 A校", "平均 B校"),
y = c(prop$add_mean_a_male_y - 5,
prop$add_mean_b_male_y - 5),
label = c(
paste0("平均 A校(男性):",
prop$add_mean_a_male_y),
paste0("平均 B校(男性):",
prop$add_mean_b_male_y))) + # 男性の平均
annotate(
geom = "text", family = "Hiragino Sans", size = 3,
x = c("平均 A校", "平均 B校"),
y = c(prop$add_mean_a_female_y + 5, prop$add_mean_b_female_y + 5),
label = c(
paste0("平均 A校(女性):", prop$add_mean_a_female_y),
paste0("平均 B校(女性):", prop$add_mean_b_female_y))) + # 女性の平均
xlab("学校と平均") + # X軸のラベル
ylab("得点") + # Y軸のラベル
scale_y_continuous(
breaks = seq(0, 100, by = 10),
limits = c(0,100),
minor_breaks = NULL) + # 縦軸の書式設定
theme_minimal(base_family = "Hiragino Sans") + # テーマとフォント
theme(legend.title = element_blank(),
axis.title.x = element_text(size = rel(1.5)),
axis.title.y = element_text(size = rel(1.5)),
axis.text.x = element_text(size = rel(1.5)),
axis.text.y = element_text(size = rel(1.5)),
panel.grid.major.x = element_blank()) # 凡例と縦軸の削除
return(g)
}
# 描画
print(my_ggplot(data, properties()))
アメリカ海軍は第二次世界大戦中，任務を終えて戻った飛行機の損傷箇所を検証
これは生存者バイアスというセレクションバイアスの一つ
某国の自治体の職業安定所は無料の職業訓練を実施している。資格取得のための講座を提供したりコンピュータースキルの研修を行ったりして，就職を支援する。
職業訓練プログラムの有効性を検証するため，一定期間の間に求職に訪れた人のうち支援を受けた人，受けなかった人それぞれ100人ずつをランダムに選んで比較することとした。
ここから，職業訓練をすることで，就職率が（70-50）/ 50 = 40%向上したと結論づけた。
この結論には問題があります。どのような問題があると考えられますか？
\[ Y_i= \beta_0 + \beta_1 X_i + \epsilon_i \tag{1}\]
という単回帰分析を考えます（\(E[\epsilon_i] = 0\)）。
ここで，説明変数が外生変数であるとは，\(X_i\)と誤差項\(\epsilon_i\)が相関しないことを意味しています。これは，
\[ \mathrm{E}[X_i\epsilon_i]=\mathrm{Cov}(X_i\epsilon_i) = 0 \]
が成立することを意味し，この性質を外生性 (exogeneity)と言います。
Equation 1 の両辺の期待値を取ると
\[ \begin{split} \mathrm{E}[Y_i] &= \beta_0 + \beta_1 \mathrm{E}[X_i] \\ \beta_0 &= \mathrm{E}[Y_i] - \beta_1 \mathrm{E}[X_i] \end{split} \]
となり，これを Equation 1 に代入して
\[ \begin{split} Y_i - \mathrm{E}[Y_i] &= \beta_1 (X_i -\mathrm{E}[X_i]) \end{split} \]
となります。ここで，両辺に\(X_i\)をかけて期待値をとったら
\[ \begin{split} \mathrm{E}[X_i ( Y_i - \mathrm{E}[Y_i]] &= \beta_1\mathrm{E}[X_i ( X_i - \mathrm{E}[X_i]] + \mathrm{Cov}(X_i\epsilon_i) \\ \mathrm{Cov}(X_iY_i) &= \beta_1\mathrm{Var}(X_i)+ \cancel{\mathrm{Cov}(X_i\epsilon_i)} \\ \beta_1 &=\frac{\mathrm{Cov}(X_iY_i) }{\mathrm{Var}(X_i)} \end{split} \tag{2}\]
となります。分散・共分散を標本分散・標本共分散に置き換えることで，実際のデータから\(\beta_1\)を推定可能です。
もし， Equation 1 の\(X_i\)が外生変数ではない，つまり\(\epsilon_i\)と相関しているとする
\[ \mathrm{E}[X_i\epsilon_i]=\mathrm{Cov}(X_i\epsilon_i) \not= 0 \]
この時，\(X_i\)は内生性(endogeneity)を持つ内生変数と言います。この時 Equation 2 において，\(\mathrm{Cov}(X_i\epsilon_i)\)が消えないので
\[ \begin{split} \beta_1 + \frac{\mathrm{Cov}(X_i\epsilon_i)}{\mathrm{Var}(X_i)} & =\frac{\mathrm{Cov}(X_iY_i) }{\mathrm{Var}(X_i)} \end{split} \]
となり，\(\mathrm{Cov}(X_i\epsilon_i) / \mathrm{Var}(X_i)\)分推定値がズレる（バイアスがかかる）ことになります。
バイアスがかかってなかったら
\[ \beta_1 =\frac{\mathrm{Cov}(X_iY_i) }{\mathrm{Var}(X_i)} \]
でした
n <- 200
e <- rnorm(n)
X <- (1 + 0.4*e) * runif(n)
b0 <- 1
b1 <- 2
Y <- b0 + X * b1 + en個作成
runif() は，[0,1]の一様分布を作成する関数。
これらを使って回帰分析を行う
lm(Y~X) |>
summary()
Call:
lm(formula = Y ~ X)
Residuals:
Min 1Q Median 3Q Max
-1.6126 -0.6132 -0.0656 0.4686 3.2316
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.1855 0.1060 1.75 0.0816 .
X 3.4862 0.1808 19.28 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9055 on 198 degrees of freedom
Multiple R-squared: 0.6525, Adjusted R-squared: 0.6507
F-statistic: 371.7 on 1 and 198 DF, p-value: < 2.2e-16切片の値は真の値1より小さく，計数の値は真の値2より大きく誤推定されている。これは，説明変数と誤差項の相関が引き起こしていて，それらの相関が正だから係数がより大きく推定されている。
もし，真のモデルが
\[ Y_i= \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + \epsilon_i \]
で，\(X_1\)と\(X_2\)がともに共に誤差項と相関しないとします。この場合，重回帰分析を行うことで，\(X_1\)と\(X_2\)が\(Y_i\)に与える影響を正しく推定できます。
ここで，\(X_2\)が得られない場合を考えます。推定に使えるのは\(X_1\)だけなので
\[ Y_i= \gamma_0 + \gamma_1 X_i + \eta_i \]
を推定することになります。この際には，
\[ E(\gamma_1)=\beta_1+\beta_2\frac{\mathrm{Cov}({X_1X_2})}{\mathrm{Var}({X_1})} \]
となり，\(\beta_2\mathrm{Cov}({X_1X_2})/\mathrm{Var}({X_1})\)分のバイアスがかかります。このバイアスは，\(\mathrm{Cov}({X_1X_2})=0\)でない限り存在します。これは，疑似相関の際に起こるバイアスを表しています。
社会調査で多く用いられる「アンケート調査」のデータは，本来測定したいものを正確に測定できていない可能性があります（アンケート調査に適当に回答した経験はありませんか？）
もし，測定したいものの測定に誤差があった場合，本来は， Equation 1 式
\[ Y_i= \beta_0 + \beta_1 X_i + \epsilon_i \]
を検証したいのに，Xが誤差のあるWでしか測定しかできないとします。
\[ W_i = X_i + u_i \]
そうすると， Equation 1 式は
\[ Y_i= \beta_0 + \beta_1 W_i + \eta_i \]
となります。ここで，\(\eta_i = \epsilon_i - \beta_1u_i\)です。\(u_i\)の期待値は0で\(X_i,\epsilon_i\)と独立と仮定します。外生性の条件である\(\mathrm{E}[W_i\eta_i]\)は
\[ \begin{split} \mathrm{E}[W_i\eta_i] &= \mathrm{E}[W_i(\epsilon_i - \beta_1u_i)] \\ &= \mathrm{E}[W_i\epsilon_i] - \beta_1 \mathrm{E}[W_iu_i] \\ &=\mathrm{E}[(X_i+u_i) \epsilon_i] - \beta_1 \mathrm{E}[(X_i+u_i)u_i] \\ &= - \beta_1 \mathrm{Var}(u_i) \end{split} \]
となるので，\(\beta_1 \not= 0\)である限り0ではない，つまり外生性が満たされなくなります。
実際，\(\beta_1\) の推定値は，
\[ \frac{\mathrm{Cov}(W_iY_i)}{\mathrm{Var}(W_i)}= \beta_1 \left( \frac{\mathrm{Var}(X_i)}{\mathrm{Var}(X_i) + \mathrm{Var}(u_i)} \right) \]
となります。
\[ 0<\left( \frac{\mathrm{Var}(X_i)}{\mathrm{Var}(X_i) + \mathrm{Var}(u_i)} \right)<1 \]
なので，\(\beta_1 > 0\)の時
\[ \beta_1 > \beta_1\left( \frac{\mathrm{Var}(X_i)}{\mathrm{Var}(X_i) + \mathrm{Var}(u_i)} \right)>0 \]
となるため，\(\beta_1\)は過小推定されます。この推定のずれは，\(\mathrm{Var}(u_i)\)が大きければ大きいほど強くなります（より過小に推定されます）。
n <- 200
e <- rnorm(n)
X <- rnorm(n)
u <- runif(n,-1,1)
W <- X + u
b0 <- 1
b1 <- 2
Y <- b0 + X * b1 +e lm(Y~W)|>
summary()
Call:
lm(formula = Y ~ W)
Residuals:
Min 1Q Median 3Q Max
-3.4083 -1.0580 0.0565 1.0832 2.9572
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.92086 0.10274 8.963 2.37e-16 ***
W 1.47199 0.08762 16.800 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.451 on 198 degrees of freedom
Multiple R-squared: 0.5877, Adjusted R-squared: 0.5856
F-statistic: 282.2 on 1 and 198 DF, p-value: < 2.2e-16真の関係よりも過小に評価されるはずです。
同時性は，従属変数と独立変数が，相互に依存している場合に起きます。
警察官の配置が犯罪抑止にどれぐらい役立つのかを検証しようとしました。地域別の警察官の配置人数と犯罪発生件数のデータを集め，地域\(i\)の警察官の数を\(X_i\)，犯罪件数を\(Y_i\)として以下のようなモデルの回帰分析を行いました。
\[ Y_i= \beta_0 + \beta_1 X_i + \epsilon_i \]
分析の結果，Xの係数は有意に正でした。
警察官の数を増やすと犯罪件数がどの程度減少するかを調べるならば， Equation 1 のように，YをXに回帰すれば良さそうです。しかし，警察官を配置すると犯罪は減少しそうですが，犯罪が多い地域に重点的に配置されそうです。つまり
\[ \left\{ \, \begin{aligned} & Y_i = \beta_0 + \beta_1 X_i + \epsilon_i \\ & X_i = \gamma_0 + \gamma_1 Y_i + u_i \end{aligned} \right. \]
ただし，\(\epsilon_i, u_i\)は相関しないものとします。ここで，上の式の外生性を確認すると
\[ \begin{split} \mathrm{E}[X_i\epsilon_i] &= \mathrm{E}[ (\gamma_0 + \gamma_1 X_i + u_i)\epsilon_i] \\ &=\mathrm{E}[Y_i\epsilon_i]\gamma_1 \end{split} \]
となり\(\gamma_1 \not=0\)となる限り0にはならず外生性は満たされません。
内生性を，データ分析の結果だけから見抜くことは無理（内生性の検定はあるけれど…）
それよりも重要なのは分析対象の知識
データだけを見て（分析対象の知識がないまま）うまく分析することはできない
n <- 200
b0 <- 1
b1 <- 2
Estimate <- \(lambda){
e <- rnorm(n)
X <- (1 + lambda * e ) * runif(n)
Y <- b0 + X * b1 + e
lm(Y~X)$coefficient
}
simulate <- \(lambda){
estimates <- matrix(0,100,2)
for(i in 1:100) estimates[i, ] <-Estimate(lambda)
colMeans(estimates)
}
lambdas <-(0:60) / 100
results <- mapply(simulate, lambdas)
bias0 <-results[1, ] -b0
bias1 <-results[2, ] -b1
#par(family= 'Hiragino Sans')
#plot(lambdas, bias0, xlab='λ', ylab = 'バイアス')
#plot(lambdas, bias1, xlab='λ', ylab = 'バイアス')
a <- tibble(lambdas,bias0,bias1)
ggplot(a,
aes(x = lambdas,
y = bias0)
) +
geom_point()+
theme(text = element_text(family = 'Hiragino Sans')) +
labs(title= "切片のバイアス",
x = 'λ',
y = 'バイアス')
ggplot(a,
aes(x = lambdas,
y = bias1)
) +
geom_point()+
theme(text = element_text(family = 'Hiragino Sans')) +
labs(title= "係数のバイアス",
x = 'λ',
y = 'バイアス')
Yに対するAの効果を知りたい
\[ Y_i = \beta_0+\beta_1A_i+u_i \]
最小二乗法*を使って推定する。
\[ \hat{\beta}_1=\sum\frac{(A_i-\bar{A})Y_i}{(A_i-\bar A)^2}=\frac{S_{AY}}{S_{AA}} \]
\[ \hat{\beta_0}=\bar{Y}-\hat{\beta_1}\bar{A} \]
ただし
\(\bar{A}=\frac{1}{n}\sum A_i\)
uに関する仮定
\(E[u_i]=0\)
\(V(u_i)=\sigma^2\)
ここで，Aと Yの関係が歪みなく推定されるためには
\(E[u|A]=0\)
(Yと関係するA以外の要因が，Aと関係ない) 時
真のモデルは
\[ Y_i=\beta_0+\beta_1A_i+\beta_2L_i+u_i \]
でも，推定するモデルは
\[ Y_i=\alpha_0+\alpha_1A_i+v_i \]
つまり，実際には含まれるべきLが含まれていない。どうなる？
推定するモデルの推定値に真のモデルを代入すると
\[ \begin{split}\hat\alpha_1&=\frac{S_{AY}}{S_{AA}} = \frac{\sum (A_i-\bar A)(Y_i-\bar Y)}{ \sum (A_i-\bar A)^2}\\&=\sum w_{Ai}Y_i \\&=\sum w_{Ai}(\beta_0+\beta_1A_i+\beta_2L_i+u_i)\\&=\beta_1+\beta_2\frac{S_{AL}}{S_{AA}}+\sum w_{2i}u_i\end{split} \]
期待値を取ると
\[ E(\alpha_1)=\beta_1+\beta_2\frac{S_{AL}}{S_{AA}} \]
\(\beta_2\frac{S_{AL}}{S_{AA}}\)の部分がLを入れなかったことによって生じる推定値のずれ（バイアス）1
\(S_{AL}=0\)でない限り不偏性が保たれないので，間違った推定値が計算される。一致性もない。
\(S_{AY} = \sum (A_i-\bar A)(Y_i-\bar Y), S_{AA} = \sum (A_i-\bar A)^2\), \(w_{Ai}=\frac{A_i - \bar A}{\sum(A_i - \bar A)}\)↩︎