--- title: "9 株式投資への応用例" subtitle: "会計発生高アノマリーの検証" date: 2025/06/13 format: html: default revealjs: output-file: 9_anomaly_slide.html bibliography: references.bib --- ## 会計利益とアクルーアルズ ### 会計利益の構成要素 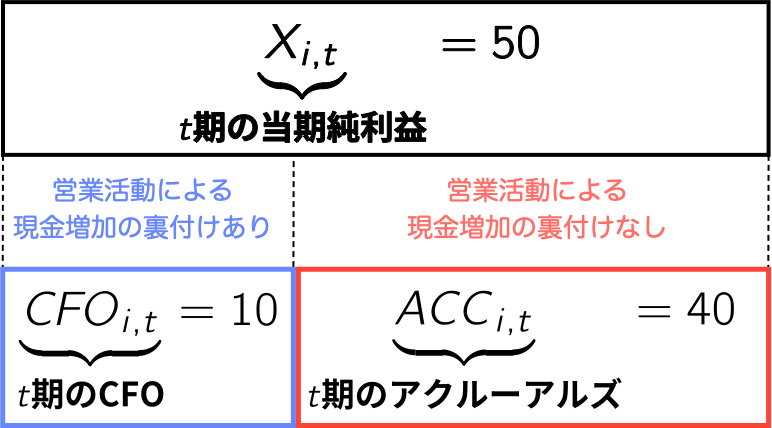 {width="50%"}- アクルーアルズと一口に言っても定義は多様.詳細は[ @larson2018 ] を参照.### CFOとアクルーアルズの持続性の相違 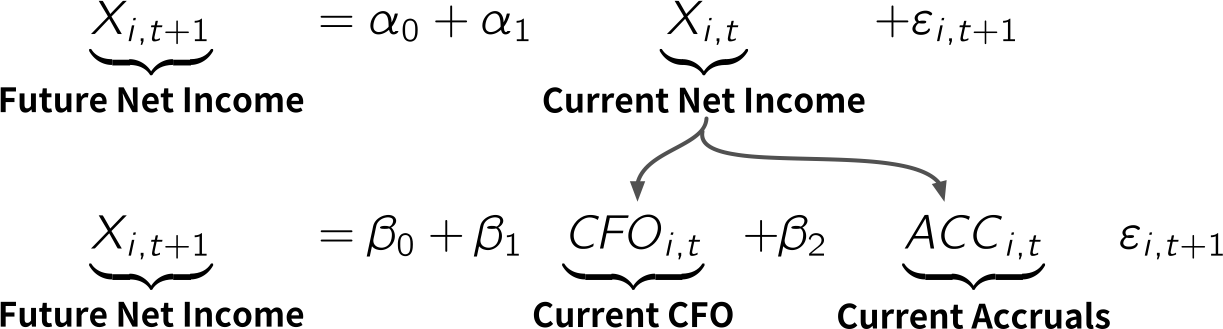 {width="60%"}- 実際,推定してみるとざっくり...\\ {\textbf{0.60}}}}### 両者を区別することなく投資すれば... 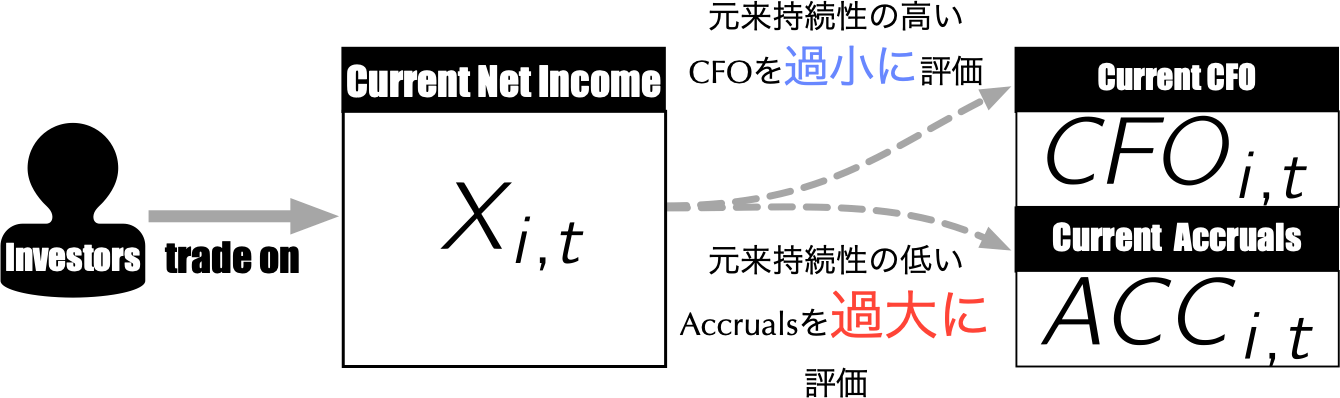 {width="60%"}- Sloan (1996)の主張 --- Stock prices are found to [ **act as if investors "fixate" on earnings** ] {style="color: blue"}, failing to reflect fully information contained in the accrual and cash flow components of current earnings...- [ **予測:** ] {style="color: red"} 過大に評価された[ $ACC_{i,t}$が大きい銘柄ほど,将来リターンは有意に低い ] {style="color: red"}.## アクルーアルズ・アノマリーの分析 ### 検証の大まかな流れ - 検証の大まかな流れは,以下の通りである. {width="80%"}### $\mathit{ACC}_{i,t}$を計算しよう 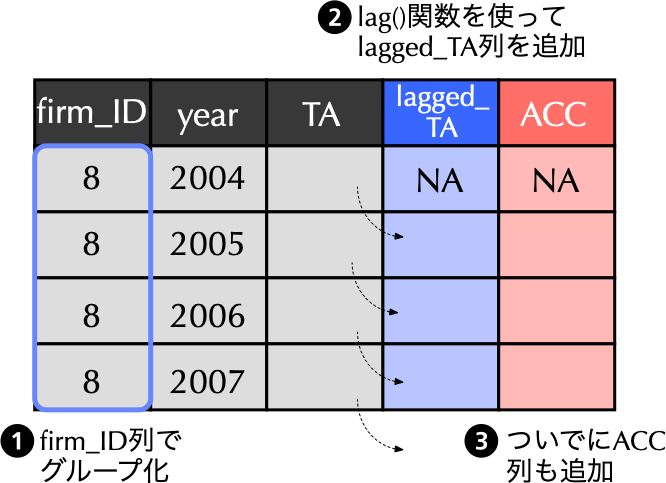 {width="50%"}### 財務データの読み込みと`ACC`の計算 - $\mathit{ACC}_{i,t}$を計算するため,`simulation_data` フォルダに格納されている財務データ`financial_data2.csv` を改めて読み込もう[ **(5行目)** ] {style="color: blue"}.- その上で,`group_by()` 関数により`firm_ID` でグループ化[ **(9行目)** ] {style="color: blue"}した後,1年前の資産合計を`lagged_TA` として計算[ **(10行目)** ] {style="color: blue"}し,$t$期のアクルーアルズ`ACC` も前スライドの定義に従って計算[ **(11行目)** ] {style="color: blue"}したのが以下のコードである.```{r} # tidyverseの読み込み :: p_load (tidyverse) # 財務データの読み込み <- read_csv ("../simulation_data/financial_data2.csv" )# アクルーアルズACCを計算し,データフレームに追加 <- financial_data %>% group_by (firm_ID) %>% # firm_IDでグループ化 mutate (lagged_TA = lag (TA), # 前期末の資産合計をlagged_TAと定義 ACC = ifelse (macc == 12 , (X - CFO) / lagged_TA, NA )) %>% # 定義に従いACCを計算 ungroup () # グループ化の解除 ``` ### 投資ユニバースの確定 #### 目標 - - [ **(1) `ACC`が計算可能** ] {style="color: red"}で,かつ,[ **(2) 3月決算企業のみ** ] {style="color: red"}を抽出し,そのデータフレームを投資ユニバース`universe` として定義しよう.```{r} # lubridateの読み込み :: p_load (lubridate) # ACCが計算可能で,かつ3月決算企業のみを抽出してuniverseとして保存 <- financial_data %>% drop_na (ACC) %>% # ACCが欠損のものを除外 filter (month (fiscal_year_end) == 3 ) # 3月決算企業のみを抽出 ``` - 初出の`lubridate` パッケージは,[ **日付型を扱うのに便利な関数を提供** ] {style="color: red"}している[ (教科書376頁) ] {style="color: red"}.- 例えば,上述のコードではYYYY-MM-DD形式で収録されている`fiscal_year_end` に`lubridate` パッケージの[ **`month()`関数を適用** ] {style="color: blue"}することにより,決算月を取り出している.### 年度ごとに十分位ポートフォリオの作成 #### 目標 - 先に作成した`universe` を用いて,[ **年度`year`ごと`ACC`の大きさに応じた十分位ランク`ACC_rank10`列を作成** ] {style="color: red"}し,それを新しいデータフレーム`ACC_rank10_data` として定義しよう.- ただし,`ACC_rank10_data` は,`firm_ID` , `year` , `ACC_rank10` の三列のみによって構成すること. - **(ヒント)** ランク分けには`dplyr` パッケージに含まれる`ntile()` 関数を使うのが便利である.`ntile()` 関数は,最初の引数としてグループ分けしたいデータ(ここでは`ACC` )を取り,その次の引数にグループの数(ここでは10)を取る. {width="50%"}### 目標を達成するためのコード例 ```{r} # 年度ごとにACCの大きさに応じて十分位ポートフォリオを作成 <- universe %>% group_by (year) %>% # 年でグループ化 mutate (ACC_rank10 = as.factor (ntile (ACC, 10 ))) %>% # 十分位ランクを作成 ungroup () %>% # グループ化の解除 select (firm_ID, year, ACC_rank10) # 必要なデータだけ残す ``` - [ **3行目:** ] {style="color: blue"} `group_by()` 関数を使って`year` でグループ化- [ **4行目:** ] {style="color: blue"} `ntile()` 関数を使って`ACC` の大きさに基づいて十分位ランク`ACC_rank10` を作成.`ntile()` 関数の返り値は整数型であることを思い出そう.十分位ランクを表す`ACC_rank10` はカテゴリカル変数[ (教科書第3.6.1節) ] {style="color: red"}であるため,ファクター型へと変換することを目的として`as.factor(ntile(ACC, 10))` を用いている.- [ **5行目:** ] {style="color: blue"} `ungroup()` 関数によってグループ化の解除.- [ **6行目:** ] {style="color: blue"} 三変数のみ選択.### クロス集計による確認 ```{r} # table()関数を用いてクロス集計 table (ACC_rank10_data$ year, ACC_rank10_data$ ACC_rank10)``` - 基本パッケージに含まれる `table()` 関数は,引数に集計対象となる変数(数値ベクトル)を与えると,[ **クロス集計の結果** ] {style="color: red"}を返してくれる.### 月次リターンデータの読み込み - 次に,分析の中心となる月次リターンデータ(`simulation_data` フォルダの`monthly_return_data.csv` )を`read_csv()` 関数により読み込もう.```{r} # 月次リターン・データの読み込み <- read_csv ("../simulation_data/monthly_return_data.csv" )head (monthly_return_data)``` - `date` : 年月 (YYYY-MM-DD形式)- `Re` : 各銘柄の無リスク金利に対する月次超過リターン ($= \underbrace{R_{i,t}}_{\textbf{銘柄iの月次リターン}} - \underbrace{R_{F,t}}_{\textbf{同月の無リスク金利}}$)### `ACC_rank10`情報結合に向けた前処理 - $t$年6月末時点でポートフォリオを組成することを鑑み,$t$年7月から$t + 1$年6月までの月次リターンデータに$t$年度の`ACC_rank10` を結合する必要がある点がポイントである. {width="75%"}- それを実現するために,次頁のコードでは`monthly_return_data` に`year` 列を追加する際,`if_else()` 関数を適用して`year` を調整している. - `date` が7月以上ならば,`date` の年をそのまま適用 - そうでなければ(`date` が6月以下ならば),`date` の年から1を差し引く### コードの実行結果 ```{r} # t年7月から運用を開始することを前提にyear列の追加 <- monthly_return_data %>% mutate (year = if_else (month (date) >= 7 , year (date), year (date) - 1 )) ```  {width="75%"}### `ACC_rank10`情報の結合 - こうして`firm_ID` と`year` をキーとして,`monthly_return_data` と`ACC_rank10_data` を結合させることができるので,`monthly_return_data` を基に`left_join()` 関数を使って`ACC_rank10_data` を結合したのが以下のコードである.```{r} # firm_IDとyearをキーに,月次リターン・データにACC_rank10情報を結合 <- monthly_return_data %>% left_join (ACC_rank10_data, c ("firm_ID" , "year" )) # 結合後のデータ確認 head (monthly_return_data) ``` ### 各ポートフォリオの運用結果を集計 - 等加重ウェイトで運用した場合の各月各ポートフォリオの実現超過リターンは,ポートフォリオ内の[ **各銘柄の超過リターンを単純平均する** ] {style="color: blue"}ことで求められる[ (等加重ポートフォリオと時価総額加重ポートフォリオとの計算方法の相違は,教科書コラム6.1参照) ] {style="color: red"}.- `date` と`ACC_rank10` でグループ化し,`summarize()` 関数を使って各ポートフォリオの運用結果を集計し,新しいデータフレーム`ACC_sorted_portfolio` を作成しよう.```{r} # 等加重ウェイトでの運用を前提に,各月各ポートフォリオの実現超過リターンを計算 <- monthly_return_data %>% group_by (date, ACC_rank10) %>% # dateとACC_rank10でグループ化 summarize (Re = mean (Re)) %>% # 月次超過リターンの平均値を計算 ungroup () # グループ化の解除 ``` ### 最小アクルーアルズ・ポートフォリオの運用結果 ```{r} # 最小アクルーアルズ・ポートフォリオの運用結果のみを抽出して表示 %>% filter (ACC_rank10 == 1 ) %>% # 最小アクルーアルズ・ポートフォリオを抽出 head () # head()関数により確認 ``` ## アルファの実務的な意味合い ### CAPMを前提としたアルファ  {width="80%"}### パフォーマンス評価尺度としてのアルファ[(教科書第6.4節)]{style="color: red"} - 証券投資の実務においては,アルファはファンド運用者の運用スキルの評価基準として利用される.- この場合,CAPMを始めとする[ **ファクター・モデル** ] {style="color: blue"}[^1] はファンド運用のリスクに応じた適切なリターンのベンチマークとして利用されており,<u>アルファはファンド運用者の固有の付加価値</u>を表すものとして,彼らの報酬決定の基準となる. {fig-align="center"}### FF3アルファの推定 - 手始めに,アクルーアルズが最小のポートフォリオ (`ACC_rank10` が`1` )のアルファを推定する方法を考えてみよう.- なお,ベンチマークとするモデルはCAPMではなく,より実践的に[ **Fama-Frenchの3ファクター・モデル** ] {style="color: blue"} (FF3モデル)としよう.そのモデルを前提とした場合のアルファ,すなわちFF3アルファは,次の回帰モデルを推定することによって求められる.\\ \textbf{実現超過リターン}}} \\ ### ファクター・データの読み込み ```{r} # ファクター・データの読み込み <- read_csv ("../simulation_data/factor_data.csv" ) head (factor_data) # head()関数を用いて確認 ``` - `date` : 年月 (YYYY-MM-DD形式)- `R_F` : 無リスク金利- `R_Me` : 市場ポートフォリオの実現超過リターン- `SMB` : サイズ・ファクターの実現リターン- `HML` : バリュー・ファクターの実現リターン### ファクター・データの結合 - `ACC_sorted_portfolio` に,先ほど読み込まれた`factor_data` を`date` をキーとして結合したのが以下のコードである.```{r} # ACC_sorted_portfolioにファクター・データを追加 <- ACC_sorted_portfolio %>% left_join (factor_data, by = "date" )head (ACC_sorted_portfolio) # ファクター・データ結合後のデータ確認 ``` ### 時系列回帰 - ここでは手始めにアクルーアルズが最小のポートフォリオ(`ACC_rank10` が`1` ) のデータのみを抽出して,先に提示した回帰モデルを推定してみよう.- これは[ **時系列回帰** ] {style="color: red"} (time-series regression)といって,個々の銘柄やポートフォリオの実現超過リターンが,市場ポートフォリオの実現超過リターンなどのファクター・リターンによってどの程度説明できるかを回帰したモデルである.### 時系列回帰の実行コード ```{r} # アクルーアルズが最小のポートフォリオのみで時系列回帰 <- ACC_sorted_portfolio %>% filter (ACC_rank10 == 1 ) %>% #最小ポートフォリオを抽出 lm (Re ~ R_Me + SMB + HML, data = .) # .を使ってlm()関数の第二引数にデータを代入 ``` - [ **2行目:** ] {style="color: blue"} これから行う線形回帰の結果を`lm_results` へと保存- [ **3行目:** ] {style="color: blue"} `filter()` 関数により,`ACC_rank10` が最小のポートフォリオのみを抽出.- [ **4行目:** ] {style="color: blue"} 線形回帰は`lm()` 関数によって実行できる.その関数は,第一引数で`∼` 演算子を用いて回帰モデルを記述(従属変数 `∼` 独立変数1 `+` 独立変数2 `+` 以降省略)し,第二引数でデータを指定.`data` 引数内で登場するピリオド(`.` ) は,パイプ演算子`%>%` を用いてデータフレームを第一引数以外に代入する場合に用いられる[ (教科書211頁) ] {style="color: red"}.### リスト形式からデータフレーム形式へ - `lm()` 関数の返り値は[ **リスト形式** ] {style="color: red"}のため,そのままだと扱いが厄介.例えば,`lm_results` の1つ目の要素には係数推定値のみが格納されている.```{r} # リスト形式のlm_resultsの1つ目の要素を参照 print (lm_results[[1 ]])``` - `broom` パッケージに含まれる`tidy()` 関数を使って,係数推定値のみならず,標準誤差,$t$値,$p$値の情報をも含んだ一つのデータフレームへ変換するのが便利である.```{r} # broomパッケージの読み込み library (broom)``` ### `tidy()`関数の挿入 ```{r} # アクルーアルズが最小のポートフォリオのみで時系列回帰 %>% filter (ACC_rank10 == 1 ) %>% #最小ポートフォリオを抽出 lm (Re ~ R_Me + SMB + HML, data = .) %>% # .を使ってlm()関数の第二引数にデータを代入 tidy () %>% # リスト形式からデータフレームへと変換 mutate (ACC_rank10 = 1 ) # 失われたACC_rank10情報を追加 ``` - [ **5行目:** ] {style="color: blue"} `broom` パッケージの`tidy()` 関数を使って,係数推定値等をデータフレームに変換している.- [ **6行目:** ] {style="color: blue"} どのポートフォリオの結果であるかが分かるように,`ACC_rank10` 列を追加.### `for`文を使って分位ごとに推定  {width="80%"}### `for`文を使ったコードの書き方 #### `for`文とは? `for (` [ **Variable Name** ] {style="color: blue"} `in` [ **Sequence** ] {style="color: green"}`) {` <br> [ **Do Something** ] {style="color: orange"} <br> `}` ```{r} # ACC_rank10ごとにFF3モデルを推定し,FF3_resultsに保存 <- list (NA ) # ①推定結果を保存するために空のリストを準備 # ②for文を使ってACC_rank10ごとに時系列回帰を行い,FF3_resultsの第i要素に代入 for (i in 1 : 10 ) {<- ACC_sorted_portfolio %>% filter (ACC_rank10 == i) %>% lm (Re ~ R_Me + SMB + HML, data = .) %>% tidy () %>% mutate (ACC_rank10 = i) ``` - 第1ポートフォリオから第10ポートフォリオまで次々に推定を行いたいわけだから`for (i = 1:10) {}` と書き,`{}` には先の第1ポートフォリオの推定コードをそのまま適用し,[ **`1`の部分を`i`に変更** ] {style="color: blue"}すれば良い.### データフレームへの統合 - 異なるポートフォリオ間で推定結果を比較するには,リスト内に格納されている各データフレームを一つのデータフレームに統合する方が便利である.`FF3_results` 内に保存されている各データフレームを[ **縦方向に統合していくには`dplyr`の`bind_rows()`関数を用いる** ] {style="color: blue"}のが簡単な方法である[^2] .```{r} # 各ポートフォリオの推定結果を一つのデータフレームに統合 <- bind_rows (FF3_results) head (binded_FF3_results) # binded_FF3_resultsの確認 ``` ### 年次換算されたFF3アルファを出力 #### 目標 - `binded_FF3_results` からFF3アルファ`(Intercept)` の結果だけ抽出し,`FF3_alpha.csv` として`tables` フォルダに出力しよう. - ただし,`estimate` 列は`FF3_alpha` に,`p.value` 列は`p_value` へと名称変更しよう. - `FF3_alpha` を年次換算するため,12を掛け,また小数第三位までが表示されるよう桁数調整. - 出力するのは,`ACC_rank10` , `FF3_alpha` , `p_value` の三変数のみ.- **(ヒント1)** `term` 列から`(Intercept)` の行だけ抽出する場合,`term` 列は文字列`<chr>` であるため,`(Intercept)` を指定する際はダブルクォーテーション (`"` )で囲み,`"(Intercept)"` とする必要がある.- **(ヒント2)** 変数の名前変更は,`rename(新しい変数名 = 古い変数名)` により可能である.### 目標を達成するためのコード例 ```{r} # FF3アルファの結果だけをまとめてFF3_alpha.csvとして保存 %>% filter (term == "(Intercept)" ) %>% # 定数項に関する推定結果のみを抽出 rename (FF3_alpha = estimate, p_value = p.value) %>% # 列名を変更 mutate (FF3_alpha = round (FF3_alpha * 12 , 3 )) %>% # 年率に換算 select (ACC_rank10, FF3_alpha, p_value) %>% # 出力したい列を指定 write_csv ("../tables/FF3_alpha.csv" ) # tablesフォルダに出力 ``` - [ **3行目:** ] {style="color: blue"} `filter()` 関数により`(Intercept)` 行のみ抽出.注意すべきは,`term` 列は文字列`<chr>` であるため,`(Intercept)` を指定する際はダブルクォーテーション (`"` )で囲む.- [ **4行目:** ] {style="color: blue"} `rename()` 関数を使って,`estimate` と`p.value` のそれぞれを適切な名前へと変更.- [ **5行目:** ] {style="color: blue"} `FF3_alpha` を年次換算するため,12を掛け,また`round()` 関数により桁数の調整も行う.- [ **6行目:** ] {style="color: blue"} `select()` 関数に出力したい列のみ選択.- [ **7行目:** ] {style="color: blue"} `write_csv()` 関数によりファイルを出力.## 参考文献 [^1]: [ **ファクター・モデルの概要については,** ] {style="color: blue"}[ **教科書第6.3.1節** ] {style="color: red"}**を参照されたい.以降では,FF3モデルを前提として話を展開していくが,リサーチデザインなど基本的な考え方は任意の線形ファクター・モデルにも応用可能である.**[^2]: 教科書では`do.call()` 関数と`rbind()` 関数を併用しているが,返り値は同じである.









