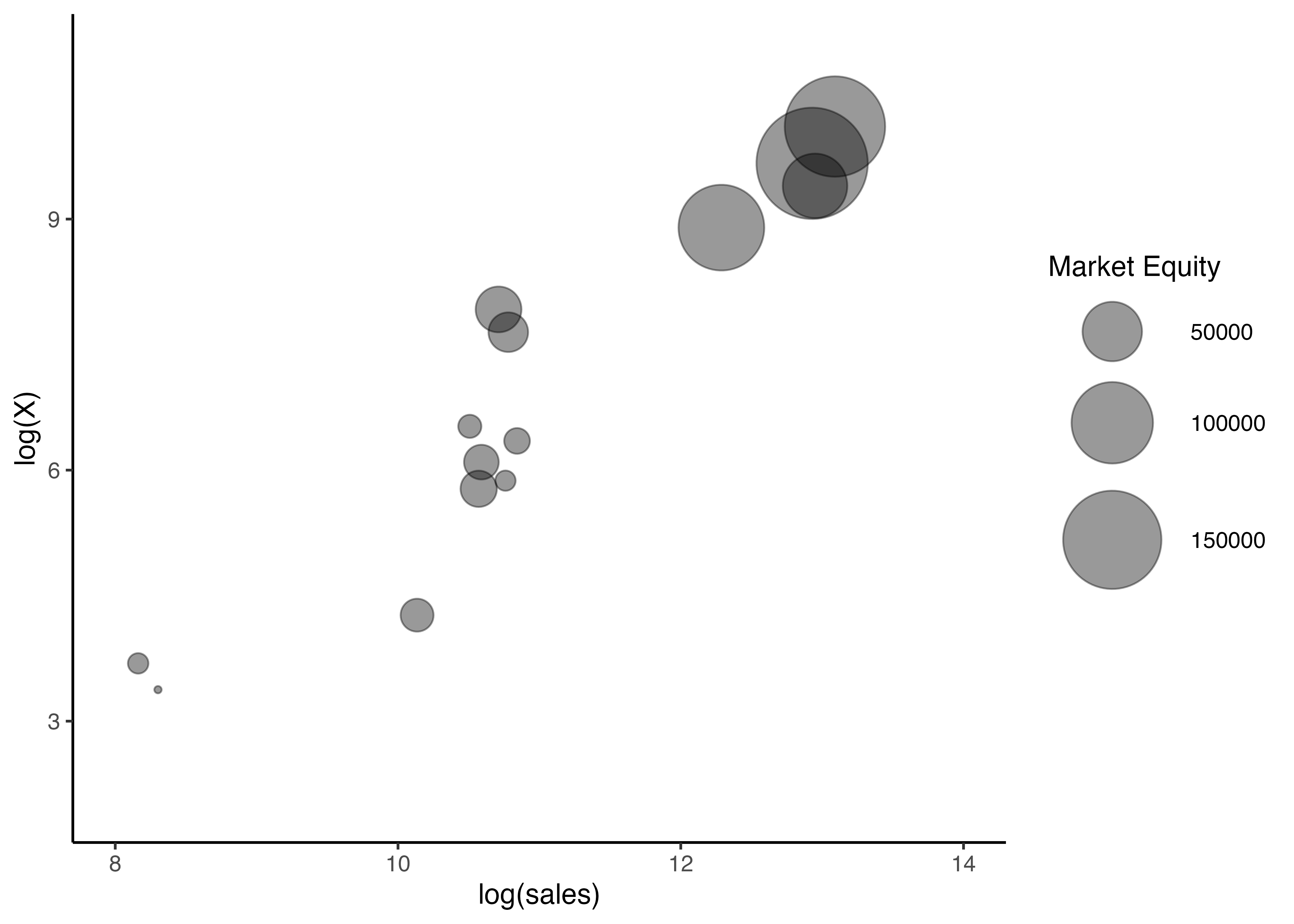
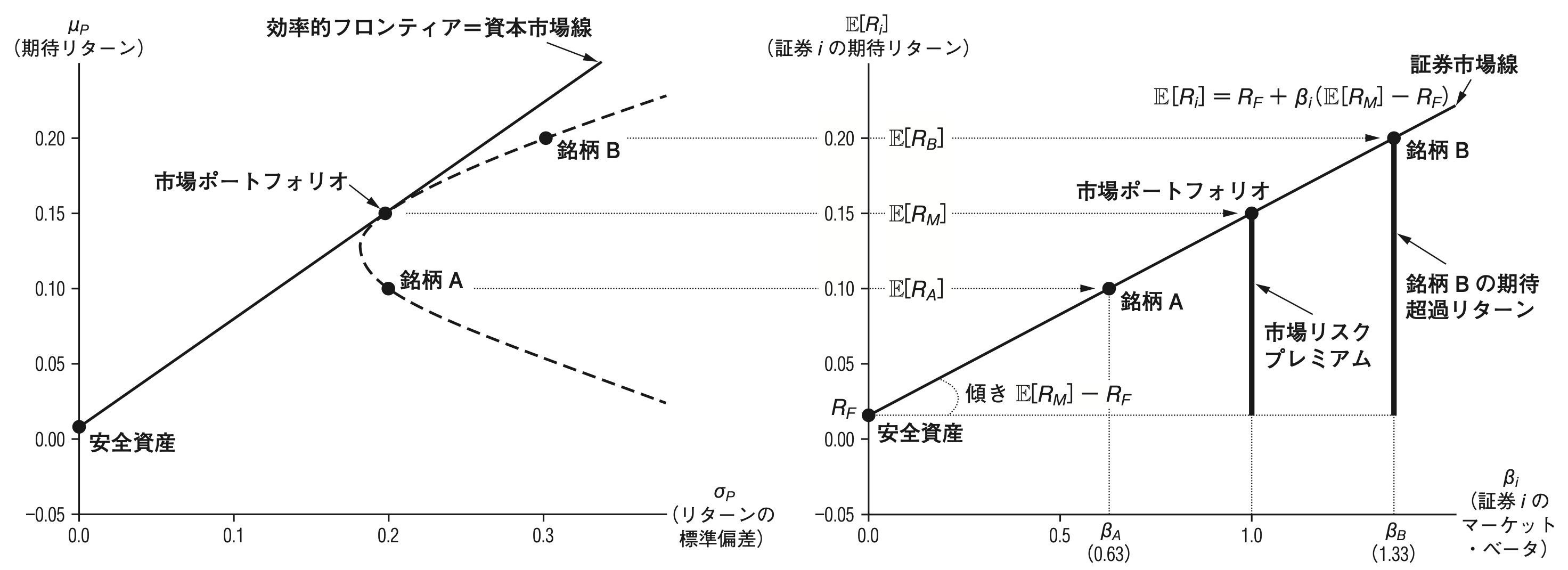
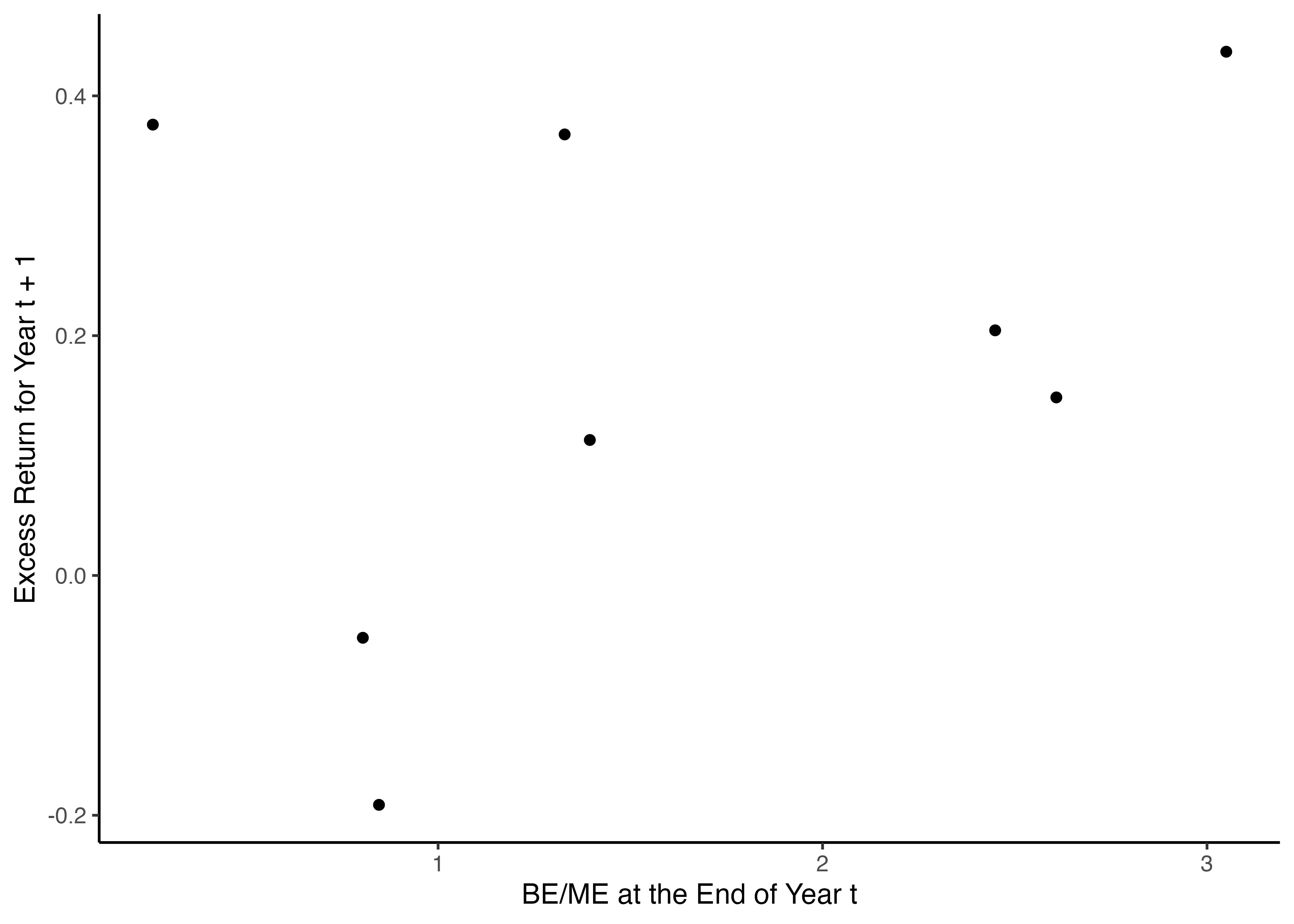
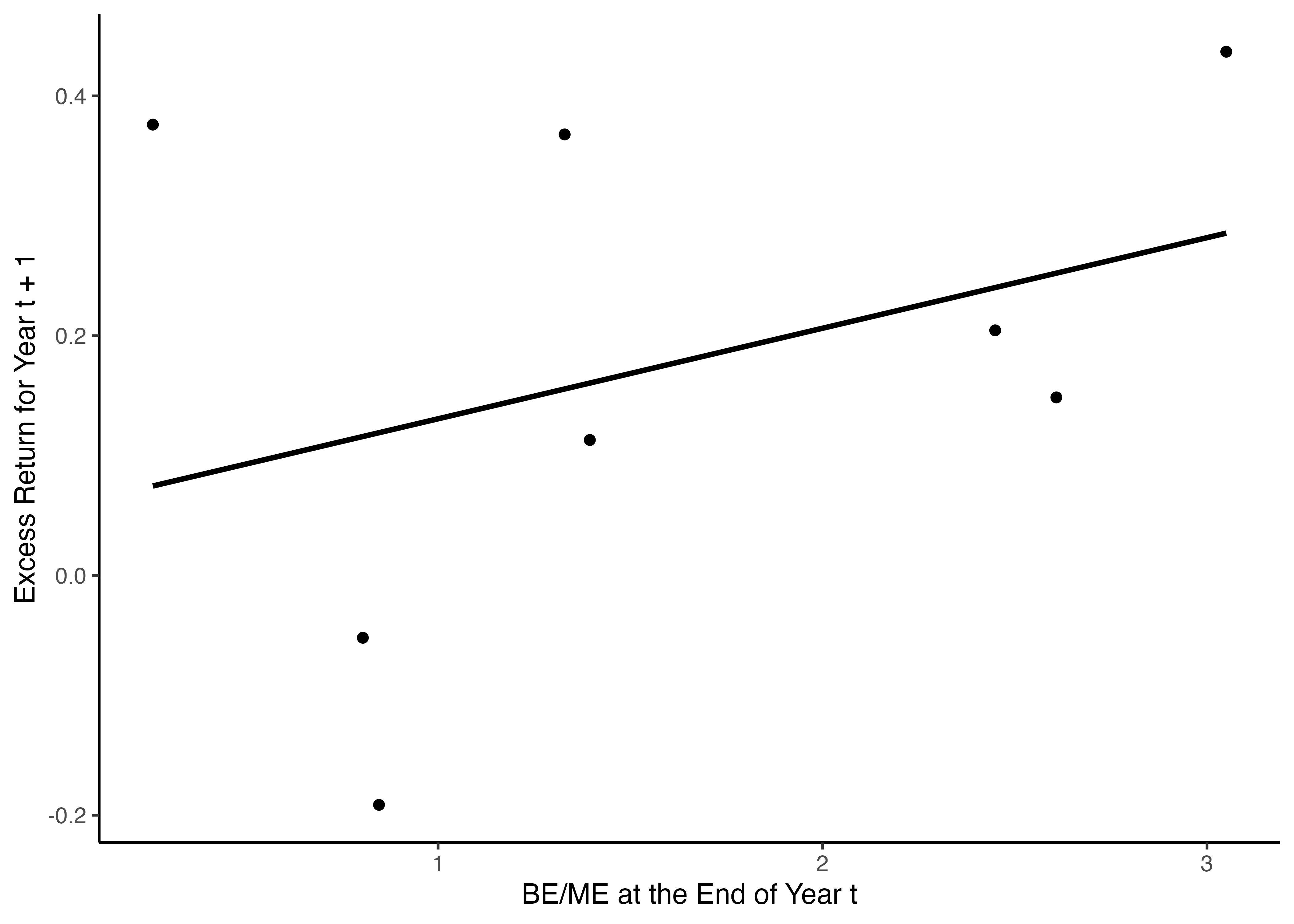
--- title: "7 財務データと株式データを組み合わせた分析" date: 2025/05/23 format: html: default revealjs: output-file: 7_earnings_stock_slide.html --- ## 株式データと財務データを組み合わせた分析(教科書第5.4節) ### 二つのデータセットを組み合わせて年次データの作成 - まずは,`full_join()` 関数を利用して,株式データ`annual_stock_data` と財務データ`financial_data` を結合し,年次のデータフレーム`annual_data` を作成してみよう.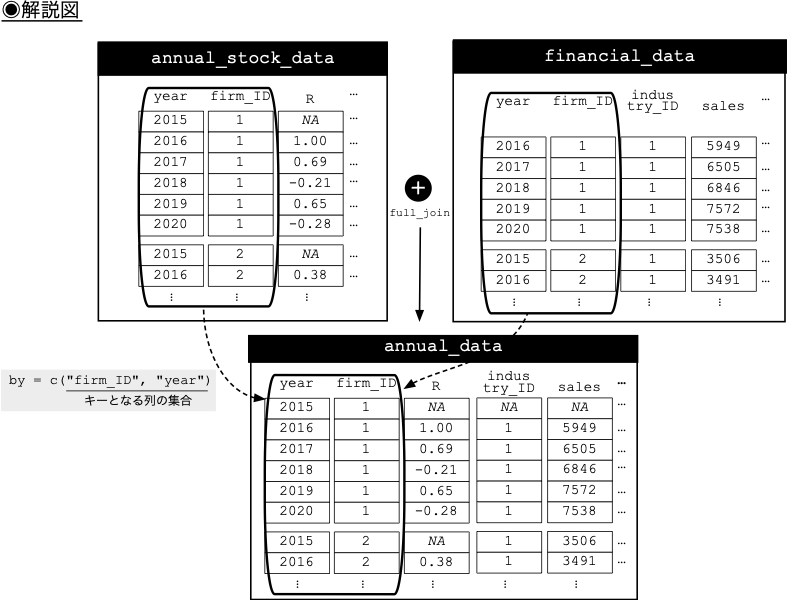 {width="80%"}```{r} :: p_load (tidyverse) # 財務データの読み込み <- read_csv ("../simulation_data/ch04_output.csv" )# 先週保存したannual_stock_data.csvを読み込み <- read_csv ("../simulation_data/annual_stock_data.csv" )# 両データフレームの結合 <- annual_stock_data %>% full_join (financial_data, by = c ("firm_ID" , "year" )) # firm_IDとyearのペアをキーとして設定 ``` ### バブル・チャートの描画 #### 目標 - まずは,`simulation_data` フォルダにある月次データ`ch05_output1.csv` を`stock_data` として読み込もう.- `stock_data` から各年の12月末時点の時価総額`ME` を抽出して,`annual_data` に追加してみよう. - **(注意点)** 財務データと株式データでは単位が違うので,`ME` に適切な処理を施して単位を統一するのを忘れずに.- その上で,`firm_ID` が`2` から`20` の企業に関して,2015年度の売上高`sales` ,当期純利益`X` ,時価総額`ME` の関係をバブルチャートで図示してみたい.$x$軸を売上高,$y$軸を当期純利益として,時価総額を円で表すことが目標である.なお,一部の大企業に影響を受けないように,売上高や当期純利益は自然対数を取り,描画する - **(注意点)** 当期純利益が赤字,すなわちマイナスの企業が散見され,そうした企業は本分析には適さないため,事前に描画対象から外しておくことを忘れずに.### 目標を実現するためのコード例 ```{r} # 月次データの読み込み <- read_csv ("../simulation_data/ch05_output1.csv" )<- stock_data %>% filter (month == 12 ) %>% # 12月のデータのみを抽出 select (year, firm_ID, ME) %>% # 追加したい列のみ選択 full_join (annual_data, ., by = c ("year" , "firm_ID" )) %>% # 年次データと結合 mutate (ME = ME / 1e6 ) # 時価総額の単位を百万円に ``` - 4 行目に登場するピリオド (`.` ) は,パイプ演算子`%>%` を用いてデータフレームを第一引数以外に代入する場合に用いられる.- 上記のコードではピリオド (`.` ) を用いてパイプ演算子から受け取ったデータフレームを第二引数に代入して,`annual_data` を`full_join()` 関数 の第一引数として扱っている.### (続)目標を実現するためのコード例 - バブルチャートを描くのには,散布図を描画するのと同様に`geom_point()` 関数を用いるが,`aes()` 関数の中に`size` 引数を追加すれば良いだけである.その関数内の`alpha` は透過度を表す引数であり,`0` から`1` までの適当な値を指定しよう.ここでは,仮に`0.4` を指定している.- `scale_size()` 関数を用いて時価総額を表す円の幅を指定している.```{r} %>% filter (year == 2015 ,%in% 2 : 20 , # firm_IDが2から20のデータを抽出 > 0 ) %>% # 対数を取るため当期純利益(X)が正のデータのみ抽出 ggplot () + geom_point (aes (x = log (sales), y = log (X), size = ME), alpha = 0.4 ) + # バブルチャートを描くにはsize引数を指定 scale_size (range = c (1 , 20 ), name = "Market Equity" ) + # range引数でバブルの最小・最大面積を指定 scale_x_continuous (limits = c (8 , 14 )) + # 両軸の範囲を指定 scale_y_continuous (limits = c (2 , 11 )) + theme_classic ()``` ## CAPM(教科書第2.4節) ### 諸仮定 ### 背後にある仮定 - [ **(選好)** ] {style="color: blue"} 全ての投資家はポートフォリオを期待値と標準偏差の基準で評価する.- [ **(取引コスト)** ] {style="color: blue"} 取引に際して手数料や税金が存在せず,空売りが自由に可能であ る.- [ **(流動性)** ] {style="color: blue"} どれだけ売買しても証券の価格は変化しない.- [ **(情報集合)** ] {style="color: blue"} 全ての投資家は同じ情報を共有している.[ **完全資本市場** ] {style="color: red"}(完全市場)と呼ぶ.「取引を行う上で完全に摩擦のない市場」といったイメージである.### CAPMの概要 #### 二つの命題 - [ **(第一命題)** ] {style="color: blue"} 市場ポートフォリオは接点ポートフォリオと一致し,効率的フロンティア(資本市場線)上に位置する.- [ **(第二命題)** ] {style="color: blue"} 各証券のリスクプレミアムは,その証券のマーケット・ベータに比例する.[ R_i\right ] -R_F}_{\textbf{証券$i$のリスクプレミアム}} & =\underbrace{\beta_i}_{\textbf{証券$i$のマーケット・ベータ}}\underbrace{\left(\mathbb{E}\left[R_M\right]-R_F\right)}_{\textbf{市場リスクプレミアム}}\\ [ R_i,\ R_M ] }{{\rm Var}[ R_M ] } ### CAPMが成立している世界におけるリスクとリターンの関係  ### その世界では,マーケット・ベータこそ全て - 第二命題は期待値に関する主張なので,実際に観察されるリターンはこれに誤差項$\varepsilon_{i,t}$が加わったものと考えることができる.\\ - 表記をシンプルとするため,$R_{i,t}^e$という記号を用いたが,これは$t$期における証券$i$の無リスク金利に対する実現超過リターン$R_{i,t}-R_{F,t}$ を意味する.### 誤差項の仮定 1. $\varepsilon_{i,t}$は独立同一分布に従う2. $\mathbb{E}[ \varepsilon_{i,t} ] = 0$3. ${\rm Cov}[ \varepsilon_{i,t}, R_{M,t}^e ] = 0$- このように定式化すると,CAPMの実証的な検証は線形回帰に帰着させることができる.つまり,超過リターンの時系列データを用意し,個別銘柄の超過リターンを市場ポートフォリオのそれで線形回帰する.- その際の[ **回帰係数がマーケット・ベータ** ] {style="color: blue"}である.### 規模効果とバリュー効果 - CAPMが成立する世界では,各銘柄のリスクプレミアムの差異は,唯一マーケット・ベータの差異によってのみ説明される.したがって,マーケット・ベータ以外の変数が,銘柄間の実現超過リターンのばらつきを説明することはないのである.- 2013年にノーベル経済学賞を受賞したユージン・ファーマ (Eugene F. Fama)や,彼の長年の共同研究者であるケネス・フレンチ (Kenneth R. French)らが行ってきた一連の研究によると,日本を含む世界中の多くの国々において,マーケット・ベータ以外の変数が,リターンの平均的な動きを説明することが明らかにされている.その中でも典型的な変数は,銘柄の規模を表す時価総額や,株主資本の簿価と時価の比である簿価時価比率 (BE/ME)である.#### 規模効果とバリュー効果 - 時価総額で測った場合の小型株ほど,また,BE/MEが高いバリュー株[^1] ほど,平均的にリターンが高い傾向にあることを明らかにしてきた.前者を[ **規模効果** ] {style="color: blue"} (size effect)と呼び,後者を[ **バリュー効果** ] {style="color: blue"} (value effect)と呼ぶ.## 線形回帰入門(教科書第5.6節) #### 目標 - `annual_data` にある全てのデータは使わず,小標本をもとに「年度末のBE/MEが高い銘柄ほど,翌年に実現する超過リターンが高い」という傾向が観察されるかの検証を試みたい.- 2016年の`firm_ID` が`10` 以下のものをサンプリングして,$n = 8$の標本を用い,線形回帰により上記の関係が観察されるか検証しよう.- まずは,最初のステップとして,前年度末の簿価時価比率`lagged_BEME` を定義し,上記の基準に沿うデータだけを抽出し,`firm_ID` , `year` , `Re` , `lagged_BEME` の四変数のみを残し,そのデータフレームを`lm_sample_data` として定義しよう.- その後,`lagged_BEME` と実現超過リターン`Re` の関係を散布図により可視化してみよう.### 簿価時価比率と株式リターンの関係を可視化 ```{r} <- annual_data %>% group_by (firm_ID) %>% mutate (lagged_BEME = lagged_BE / lag (ME)) %>% # 前年度の簿価時価比率を計算 ungroup () %>% filter (year == 2016 , # firm_IDが1から10までの企業の2016年のデータを抽出 <= 10 ) %>% select (firm_ID, year, Re, lagged_BEME) %>% # 必要な列のみ抽出 drop_na () # 欠損データを削除 ggplot (lm_sample_data) + geom_point (aes (x = lagged_BEME, y = Re)) + # x軸に簿価時価比率, y軸に超過リターン labs (x = "BE/ME at the End of Year t" , y = "Excess Return for Year t + 1" ) + theme_classic ()```  {width="80%"}### 線形関係を想定 - 出力された散布図を見てみると,全体として右肩上がりの分布となっており,両者の間には何らかの直線関係で表すことができる関係,すなわち,線形関係が存在しうる.そこで,次は実際に両者の間に線形関係を想定して,観察されたデータに最も適合する一本の直線を描いてみよう.- 以下では,`geom_smooth()` 関数を用いて,散布図上に新しく直線を追加している.この関数の引数を見てみると,`method` 引数で指定されている`"lm"` は`linear model` (線形モデル)の略で,以下で詳細に説明する線形回帰を用いて直線を描くよう指定している.```{r} ggplot (lm_sample_data) + geom_point (aes (x = lagged_BEME, y = Re)) + geom_smooth (aes (x = lagged_BEME, y = Re), method = "lm" , se = FALSE , color = "black" ) + # 回帰直線を追加するにはgeom_smooth()関数を用いる labs (x = "BE/ME at the End of Year t" , y = "Excess Return for Year t + 1" ) + theme_classic ()``` ### 出力結果  {width="50%"}- 年度末のBE/MEが1単位増加すれば,翌年の超過リターンが約0.076ポイント増加するという関係があることが分かる.- $(x_{i}, y_{i})~(i = 1, 2, \ldots, 8)$の全てが直線上に全ての点が並ぶわけではないので,各々のデータは,(a) 直線によって説明できる部分と(b)直線によって説明できない部分に分けられるのである.したがって,八つのデータの全てを適切に描写するのは,次のような式である. $$[ **残差** ] {style="color: red"} (residual)と呼ばれる.### 線形回帰モデルの導入 - 翌年のリターンと年度末のBE/MEを$y$と$x$に見立て,両者の関係を直線で表そうとした.この直線のことを線形モデルと呼ぶ.- そのモデルこそが,上式であり,モデルによって説明される変数$y$のことを[ **被説明変数** ] {style="color: blue"}(従属変数)と呼び,他方,説明に利用する変数$x$のことを[ **説明変数** ] {style="color: blue"}(独立変数)と呼ぶ.- 被説明変数の平均的な動きの説明を試みようとする線形回帰モデルでは,残差$e_{i}$を不規則な動きをする確率変数の実現値として捉える.そして,その確率変数のことを[**誤差項**]{style="color: blue"} (error term)とか,単に誤差と呼び,残差と区別するために$\varepsilon_{i}$として定義しよう.一般に線形回帰モデルでは,誤差項をうまくモデルに取り入れて,$(X_i, Y_i)$の間に以下のような関係が成立すると想定する. $$- ここで取り上げた例だと,$X_i$は$t$年度末の簿価時価比率$\mathit{BE/ME}_{i,t}$で,$Y_i$は$t+1$年の無リスク金利に対する超過リターン$R_{i,t+1}^e=R_{i,t+1} - R_{F,t+1}$,添字の$i$は`firm_ID` に該当する.したがって,より具体的に書けば, $$- (\ref{eq:linear_model})式において,$(\beta_0, \beta_1)$は回帰係数と呼ばれ,$X_i$と$Y_i$の線形関係を表すパラメータである.- 回帰係数の値はデータから直接観察することはできないので,線形回帰モデルではその推定値が関心の対象となる.- 例えば,先ほどの散布図では,$\hat{\beta}_0 \approx 0.055$,$\hat{\beta}_1 \approx 0.076$であるが,ここで$(\hat{\beta}_0, \hat{\beta}_1)$という変数名を使ったのは,$(\beta_0, \beta_1)$の推定値であることを強調するためである.### 最小二乗推定量 - 観察されたデータから$(\beta_0, \beta_1)$を推定する方法として最もよく用いられるのが[ **最小二乗法** ] {style="color: blue"} (Ordinary Least Squares),略してOLSである.\{ Y_i - ({\beta_0} + {\beta_1} X_i ) \right\} ^2 \{ Y_i - (\hat{\beta}_0 + \hat{\beta}_1 X_i ) \right\} ^2[ **最小二乗推定量** ] {style="color: blue"}$(\hat{\beta}_0, \hat{\beta}_{1})$によって,未知の回帰係数$(\beta_0, \beta_{1})$を推定する.### OLSの実装 - `lm()` 関数では,第一引数で`~` 演算子を用いて回帰モデルを記述する.- 同一のデータフレームに属する列同士で線形回帰を行う場合,`data` 引数でそのデータフレームそのものを指定すると,回帰モデルではデータフレーム名は省略して,列名のみの記述が可能になる. `lm()` 関数は,返り値として[ **名前付きのリスト** ] {style="color: blue"}を返すので,以下では`names()` 関数を用いて,その一覧を表示させている.```{r} <- lm (Re ~ lagged_BEME, data = lm_sample_data) # ~の左に従属変数, 右に独立変数を記す names (lm_results)``` - `lm()` 関数で計算した回帰係数を確認するためには,リスト`lm_results` 内の一つ目の要素を`print()` 関数により表示すれば良い.リストの要素へのアクセスの仕方は,第2回資料を参照.```{r} print (lm_results[[1 ]])``` - なお,名前付きリストに限れば,`$` 演算子を使って以下のようにアクセスすることも可能.```{r} print (lm_results$ coefficients)``` ### `broom`パッケージを利用した結果の確認方法 - `lm()` 関数は線形回帰の結果をリスト形式で詳細に返す.ただし,返り値がリストのままだと分析が不便であるので,代わりに外部パッケージの`broom` を用いて,データフレームに変換しよう.- 例えば,係数の推定値や標準誤差,$t$値,$p$値をデータフレーム形式で得るために,`tidy()` 関数が準備されている.```{r} # broomパッケージの読み込み :: p_load (broom)# lm_resultsをデータフレーム形式に変換 tidy (lm_results) ``` ### 様々な種類の回帰モデルと結果の解釈 - 今期の研究開発投資を$X_{i}$,翌期の売上高を$Y_{i}$に見立て(単位はいずれも百万円),それぞれのモデルをOLSによって推定した結果をどのように解釈すべきか考えてみよう.- 以下の表で示すとおり,いずれのモデルを前提にしても,有意水準を1%と定めたとき,$\hat{\beta}_{1}$は統計的に有意に正であり,今期の研究開発投資は,翌期の売上高向上に繋がることが分かる.その一方で,モデルによって$\hat{\beta}_{1}$の推定値やその解釈は異なる点に注意してほしい.[^1]: 株主資本や利益など,企業のファンダメンタルズを表す数値をベンチマークとして株価(延いては時価総額)が割安な銘柄をバリュー株と呼び,その対極にあるのはグロース株と呼ぶ.