Code
pacman::p_load(tidyverse)
# 株式データの読み込み
stock_data <- read_csv("../simulation_data/ch05_stock_data.csv") 2025/05/16
2025/02/23
simulation_dataフォルダ内に格納している株式データch05_stock_data.csvを読み込もう.stock_dataに格納されている各変数stock_price: 月末時点での終値DPS: 一株当たり配当額 (Dividend Per Share; DPS)shares_outstanding: 月末時点での発行済株式数adjustment_coefficient: 調整係数R_F: 月次無リスク金利\[ \text{配当性向}_{t+1} = \frac{D_{t+1}}{X_{t+1}} \]
\[ \text{DOE}_{t+1} = \frac{D_{t+1}}{Y_{t}} \] - 分母の1株当たり株主資本は,期首期末の平均 (\(=(Y_{t}+Y_{t+1})/2\))を採用したり,期末の\(Y_{t+1}\)を採用する場合などもある.
month_ID %in% 27:30はmonth_IDが27, 28, 29, 30を含んでいるという意味.DPSであるが,権利確定月,及び一株当たりの受け取り配当を記録するデータである.firm_IDが1の企業について見てみると,2017年6月の月末時点の株主に対して,一株当たり43円の配当が支払われたことが分かる.1以外の値を取る例adjustment_coefficientは,株式分割や併合などに伴う株式数の変化を調整するためのデータである.2として,リターンを計算する際に調整する必要がある.stock_dataに時価総額ME列をmutate()関数を使って追加してみよう.\[ R_t = \frac{({\rm stock\_price}_t + {\rm DPS}_t) \times {\rm adjustment\_coefficient}_t - {\rm stock\_price}_{t-1}}{{\rm stock\_price}_{t-1}} \label{eq:definition_R} \tag{5.1} \]
lagged_stock_priceを定義してから,(5.1)式に基づいて月次のトータル・リターンRをデータフレームstock_dataに追加している.ここで,\(R_{F,t}\)は同期間に安全資産で運用した場合のネット・リターンを指し,\(R_{t}^e\)の\(e\)は超過を意味するexcessの略である.
# 月次超過リターンの追加も加える
stock_data <- stock_data %>%
group_by(firm_ID) %>%
mutate(lagged_stock_price = lag(stock_price)) %>% # 前月株価をlagged_stock_priceと定義
ungroup() %>%
mutate(R = ((stock_price + DPS) * adjustment_coefficient - lagged_stock_price) / lagged_stock_price, # (5.1)式に従って月次リターンを計算
Re = R - R_F) # 月次超過リターンを計算\[ \begin{align*} \underbrace{\left(\frac{W_{\text{3月}}}{W_{\text{12月}}}\right)}_{\textbf{グロスの3ヶ月間のリターン}} = \underbrace{\left(\frac{\cancel{W_{\text{1月}}}}{W_{\text{12月}}}\right)}_{1 + R_{\text{1月}}} \times \underbrace{\left(\frac{\cancel{W_{\text{2月}}}}{\cancel{W_{\text{1月}}}}\right)}_{1 + R_{\text{2月}}} \times \underbrace{\left(\frac{W_{\text{3月}}}{\cancel{W_{\text{2月}}}}\right)}_{1 + R_{\text{3月}}} \end{align*} \]
\[ \begin{align*} \underbrace{\left(\frac{W_{\text{翌年12月末}}}{W_{\text{12月末}}}\right)}_{\textbf{グロスの年次リターン}} & = (1 + R_{\text{1月}})\times (1 + R_{\text{2月}})\times \cdots \times (1 + R_{\text{12月}}) \nonumber\\ & = \prod_{t = \text{1月}}^{\text{12月}}(1 + R_{t}) \end{align*} \]
stock_dataを基に,新しくannual_stock_dataというデータフレームを作成し,各銘柄の年次リターン,及びそれに対応する年次超過リターンをネットで計算してみよう.annual_stock_dataは,firm_ID, year, R, Re, R_Fの五変数で構成されるようにすること.simulation_dataフォルダにannual_stock_data.csvとして出力しておこう.(ヒント1) ネットの年次リターンは,単純にグロスの年次リターンから1を差し引けば良い.
(ヒント2) 各要素の積は,prod()関数により求めることができる.
以下のコードでは,group_by()関数を用いてfirm_ID,及びyearの各ペアに関して,stock_dataをグループ化し,summarize()関数を用いて年次リターンR,及びそれに対応する年次無リスク金利R_Fを計算した後,年次超過リターンReを定義している.
# 月次リターンを累積して年次リターンを計算
annual_stock_data <- stock_data %>%
group_by(firm_ID, year) %>% # firm_IDとyearのペアでグループ化
summarize(R = prod(1 + R) - 1, # バイ・アンド・ホールドの年次リターン
R_F = prod(1 + R_F) - 1) %>%
mutate(Re = R - R_F) %>% # 年次超過リターンの計算
select(firm_ID, year, R, Re, R_F) %>% # 必要な変数のみ選択
ungroup()
# head()関数により確認
head(annual_stock_data)firm_IDが1の銘柄の月次超過リターン\(R_{1,t}^e\)は,期待値の意味でゼロより大きいだろうか?
drop_na()関数を利用して欠損値を除去した後の月次超過リターンのベクトルをRe_firm_ID_1として定義している.# 月次超過リターンの期待値に関するt検定 (1)
Re_firm_ID_1 <- stock_data %>%
filter(firm_ID == 1) %>% # firm_IDが1の企業のみ抽出
select(Re) %>% # 月次超過リターンのみ抽出
drop_na() %>% # 欠損値を削除
unlist() # データフレームからベクトルに変換
mu0 <- 0 # 帰無仮説を期待値0と設定
n <- length(Re_firm_ID_1) # 標本サイズ
t_value <- (mean(Re_firm_ID_1) - mu0) / sqrt(var(Re_firm_ID_1) / n) # 定義に従ってt値を計算
## [1] 2.121296t.test()関数が用意されている.---
title: "6 株式データ分析入門"
date: 2025/05/16
format:
html: default
revealjs:
output-file: 6_stock_slide.html
---
## Rを利用した株式データ分析入門(教科書第5.1節)
### 株式データの読み込み
- まずは,`simulation_data`フォルダ内に格納している株式データ`ch05_stock_data.csv`を読み込もう.
```{r}
pacman::p_load(tidyverse)
# 株式データの読み込み
stock_data <- read_csv("../simulation_data/ch05_stock_data.csv")
```
------------------------------------------------------------------------
### `stock_data`に格納されている各変数
```{r}
head(stock_data)
```
- `stock_price`: 月末時点での終値
- `DPS`: 一株当たり配当額 (Dividend Per Share; DPS)
- `shares_outstanding`: 月末時点での発行済株式数
- `adjustment_coefficient`: 調整係数
- `R_F`: 月次無リスク金利
------------------------------------------------------------------------
### (余談)日本企業が採用する配当政策
- [**安定配当政策**]{style="color: blue"}・・・日本企業の多くが採用していた伝統的な配当政策.業績に関わらず,毎期一定の配当を支払うことを目標にする考え方.
- 代表例:井村屋(年一回1株当たり28円)
- [**配当性向 (payout ratio)政策**]{style="color: blue"}・・・業績に応じて,配当額を変化させる考え方
- 代表例:伊藤忠商事(配当性向目標30%)
{width="60%"}
::: {.callout-note icon="false"}
#### $t+1$期の配当性向 ($\text{配当性向}_{t+1}$)の計算方法
$$
\text{配当性向}_{t+1} = \frac{D_{t+1}}{X_{t+1}}
$$
:::
- 例えば,東京エレクトロンは,両者を組合せて配当性向50%を目処とするとともに,安定的に還元するため,1株当たりの年間配当金は50円を下回らないようにしている.
### 近年では,DOEを意識する企業も
- [**株主資本配当率 (Dividend on Equity ratio; DOE)政策**]{style="color: blue"}・・・1株当たりの株主資本に対して,一定の割合の配当を支払うことを目標にする考え方
- 代表例:エーザイ(DOE目標15%)
::: {.callout-note icon="false"}
#### $t+1$期のDOE ($\text{DOE}_{t+1}$)の計算方法
$$
\text{DOE}_{t+1} = \frac{D_{t+1}}{Y_{t}}
$$ - 分母の1株当たり株主資本は,期首期末の平均 ($=(Y_{t}+Y_{t+1})/2$)を採用したり,期末の$Y_{t+1}$を採用する場合などもある.
:::
- 一般的に,利益よりも株主資本の方が分散が少ないので,配当性向政策を採用する企業よりも,DOE政策を採用する企業の方が,安定的な配当が見込める.
------------------------------------------------------------------------
### 配当支払いの例
```{r}
stock_data %>%
filter(firm_ID == 1 & month_ID %in% 27:30)
```
- `month_ID %in% 27:30`は`month_ID`が`27`, `28`, `29`, `30`を含んでいるという意味.
- 6列目の`DPS`であるが,権利確定月,及び一株当たりの受け取り配当を記録するデータである.
- 例えば,`firm_ID`が`1`の企業について見てみると,2017年6月の月末時点の株主に対して,一株当たり43円の配当が支払われたことが分かる.
------------------------------------------------------------------------
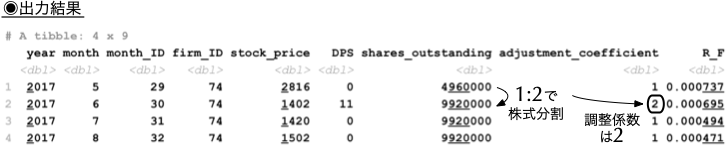
### 調整係数が`1`以外の値を取る例
```{r}
#| eval: false
stock_data %>%
filter(firm_ID == 74 & month_ID %in% 29:32)
```
{width="60%"}
- 8列目の`adjustment_coefficient`は,[**株式分割や併合などに伴う株式数の変化を調整するためのデータ**]{style="color: blue"}である.
- 例えば,株式分割により旧1株が新しく2株になったとしよう.理論株価は半分になる一方で,元の株主はそれを相殺するように2倍の株式数を手にする.ここで単純に株価だけを用いてプライス・リターンを計算してしまうと,株主の資産の変化を誤って捉えてしまう.したがって,この場合は調整係数を`2`として,リターンを計算する際に調整する必要がある.
::: callout-tip
#### プライス・リターンとは?
- 株価の変化のみに着目したリターンであり,月次$t$の株価を$P_{t}$と表すと以下のように計算することができる. $$
\frac{P_{t} - P_{t-1}}{P_{t-1}}
$$
:::
------------------------------------------------------------------------
### 時価総額の計算
- データフレーム`stock_data`に時価総額`ME`列を`mutate()`関数を使って追加してみよう.
```{r}
stock_data <- stock_data %>%
mutate(ME = stock_price * shares_outstanding)
```
------------------------------------------------------------------------
### トータル・リターンの計算
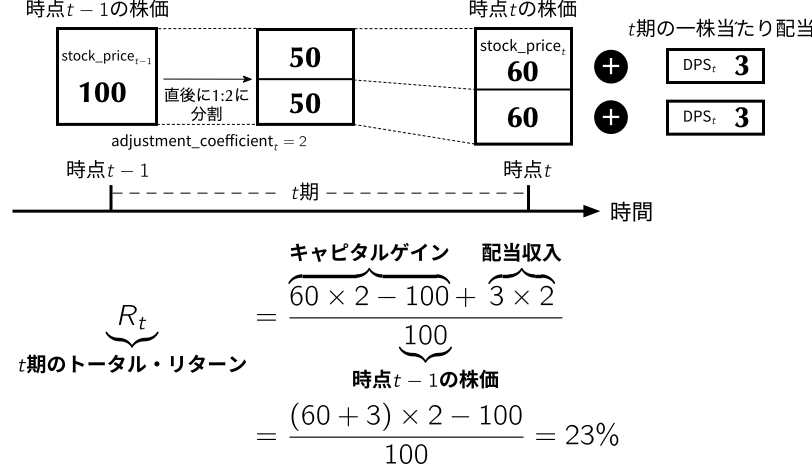
- ここで計算するリターンはトータル・リターンや配当込みリターンと言われ,[**株価の変化に加え配当収入も加味したリターン**]{style="color: blue"}である.
- 例えば,ある投資家が保有する銘柄が株式分割を行ったとしよう.定義より,月末時点でその投資家は元の保有株数の${\rm adjustment\_coefficient}_t$倍の株式を保有することになる.そして,ポートフォリオの時価評価は一株当たり${\rm stock\_price}_t$であり,更に${\rm DPS}_t$の配当を受け取る.したがって,この株式の$t$期のトータル・リターンは以下のように計算できる.
::: {.callout-note icon="false"}
#### トータル・リターンの計算式
$$
R_t = \frac{({\rm stock\_price}_t + {\rm DPS}_t) \times {\rm adjustment\_coefficient}_t - {\rm stock\_price}_{t-1}}{{\rm stock\_price}_{t-1}} \label{eq:definition_R} \tag{5.1}
$$
:::
{width="80%"}
------------------------------------------------------------------------
### 月次リターンの計算を実現するコード例
- 以下のコードでは,先に前月株価`lagged_stock_price`を定義してから,(5.1)式に基づいて月次のトータル・リターン`R`をデータフレーム`stock_data`に追加している.
```{r}
# 月次リターンの追加
stock_data <- stock_data %>%
group_by(firm_ID) %>%
mutate(lagged_stock_price = lag(stock_price)) %>% # 前月株価をlagged_stock_priceと定義
ungroup() %>%
mutate(R = ((stock_price + DPS) * adjustment_coefficient - lagged_stock_price) / lagged_stock_price) # (5.1)式に従って月次リターンを計算
```
------------------------------------------------------------------------
### 様々なリターンの定義(教科書コラム2.1)
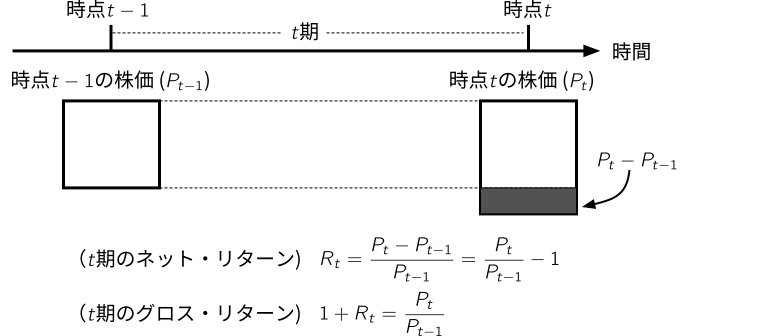
- 例えば,昨日の株価が100円で,今日の株価が110円になった場合,ネット・リターンは10% ($=$ 0.1)である.一方,[**元本分も含める場合はグロス・リターン**]{style="color: blue"}と呼び,ネット・リターンに1を足して110% ($=$ 1.1)となる.
- 単純にリターンと言った場合にどちらを指すかは文脈によるが,本書では原則としてネット・リターンの意味で用いる.
{width="80%"}
------------------------------------------------------------------------
### 無リスク金利に対する超過リターンの計算
- ネット・リターンから無リスク金利を差し引いた値を,[**(無リスク金利に対する)超過リターン**]{style="color: red"}と呼ぶ. $$
\text{($t$期の超過リターン)~~~~~} R_{t}^e = R_{t}-R_{F,t}
$$
ここで,$R_{F,t}$は同期間に安全資産で運用した場合のネット・リターンを指し,$R_{t}^e$の$e$は超過を意味するexcessの略である.
```{r}
# 月次超過リターンの追加も加える
stock_data <- stock_data %>%
group_by(firm_ID) %>%
mutate(lagged_stock_price = lag(stock_price)) %>% # 前月株価をlagged_stock_priceと定義
ungroup() %>%
mutate(R = ((stock_price + DPS) * adjustment_coefficient - lagged_stock_price) / lagged_stock_price, # (5.1)式に従って月次リターンを計算
Re = R - R_F) # 月次超過リターンを計算
```
------------------------------------------------------------------------
## リターンの累積(教科書第5.3節)
### バイ・アンド・ホールド・リターンの考え方 - 1ヶ月間を例に
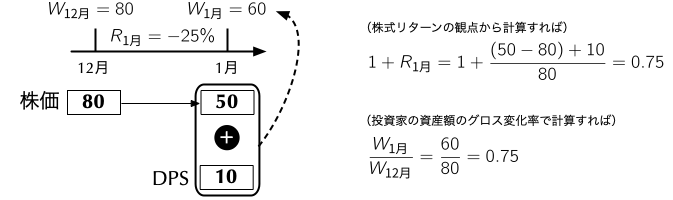
- 例えば,ある銘柄に12月末に投資をして,1ヶ月保有し続けた場合の1ヶ月間のリターンを考えてみよう.この例のように,一度投資すれば,後は売買することなく保有し続けた場合のリターンのことを明示的に強調するために,[**バイ・アンド・ホールド・リターン**]{style="color: blue"} (buy-and-hold return)と呼ぶ.
- バイ・アンド・ホールド・リターンは元本を再投資し続けた場合のリターンと言い換えられるので,[**運用を継続することによる複利の効果を反映**]{style="color: red"}した値である.
{width="80%"}
------------------------------------------------------------------------
### バイ・アンド・ホールド・リターンの考え方 - 3ヶ月間を例に
- 1ヶ月が3ヶ月に伸びたところで同じように考えることができる.すなわち,バイ・アンド・ホールドで3ヶ月間のリターンを累積するには,12月末から3月末にかけての投資家の資産額の変化率を計算すれば良い.ここでのポイントは,[**(得られた配当はすぐにその同銘柄に再投資すると考える限りにおいて)**]{style="color: blue"}資産額のグロス変化率は,以下のように積の形で分解できる点である.
$$
\begin{align*}
\underbrace{\left(\frac{W_{\text{3月}}}{W_{\text{12月}}}\right)}_{\textbf{グロスの3ヶ月間のリターン}} = \underbrace{\left(\frac{\cancel{W_{\text{1月}}}}{W_{\text{12月}}}\right)}_{1 + R_{\text{1月}}} \times \underbrace{\left(\frac{\cancel{W_{\text{2月}}}}{\cancel{W_{\text{1月}}}}\right)}_{1 + R_{\text{2月}}} \times \underbrace{\left(\frac{W_{\text{3月}}}{\cancel{W_{\text{2月}}}}\right)}_{1 + R_{\text{3月}}}
\end{align*}
$$
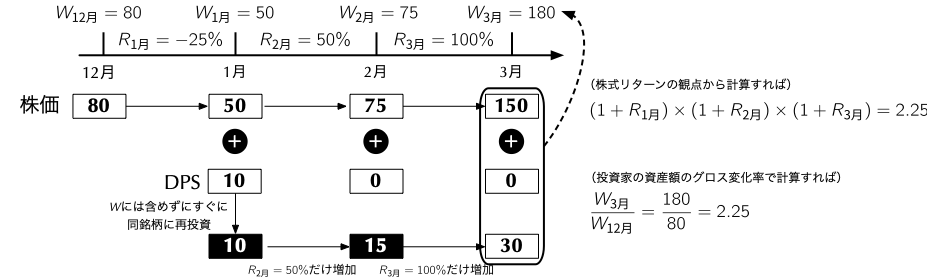{width="80%"}
------------------------------------------------------------------------
### バイ・アンド・ホールド・リターンの計算 - 12ヶ月間を例に
- 月次リターンを年次リターンに累積するには,上の計算例を3ヶ月から12ヶ月に伸ばすだけで良いことが分かるだろう.
$$
\begin{align*}
\underbrace{\left(\frac{W_{\text{翌年12月末}}}{W_{\text{12月末}}}\right)}_{\textbf{グロスの年次リターン}} & = (1 + R_{\text{1月}})\times (1 + R_{\text{2月}})\times \cdots \times (1 + R_{\text{12月}}) \nonumber\\
& = \prod_{t = \text{1月}}^{\text{12月}}(1 + R_{t})
\end{align*}
$$
::: {.callout-note icon="false"}
#### 目標
- `stock_data`を基に,新しく`annual_stock_data`というデータフレームを作成し,各銘柄の年次リターン,及びそれに対応する年次超過リターンを**ネット**で計算してみよう.`annual_stock_data`は,`firm_ID`, `year`, `R`, `Re`, `R_F`の五変数で構成されるようにすること.
- こうして完成したデータフレームを次週の講義に備えて,`simulation_data`フォルダに`annual_stock_data.csv`として出力しておこう.
**(ヒント1)** ネットの年次リターンは,単純にグロスの年次リターンから1を差し引けば良い.
**(ヒント2)** 各要素の積は,`prod()`関数により求めることができる.
:::
------------------------------------------------------------------------
### 目標を実現するためのコード例
以下のコードでは,`group_by()`関数を用いて`firm_ID`,及び`year`の各ペアに関して,`stock_data`をグループ化し,`summarize()`関数を用いて年次リターン`R`,及びそれに対応する年次無リスク金利`R_F`を計算した後,年次超過リターン`Re`を定義している.
```{r}
# 月次リターンを累積して年次リターンを計算
annual_stock_data <- stock_data %>%
group_by(firm_ID, year) %>% # firm_IDとyearのペアでグループ化
summarize(R = prod(1 + R) - 1, # バイ・アンド・ホールドの年次リターン
R_F = prod(1 + R_F) - 1) %>%
mutate(Re = R - R_F) %>% # 年次超過リターンの計算
select(firm_ID, year, R, Re, R_F) %>% # 必要な変数のみ選択
ungroup()
# head()関数により確認
head(annual_stock_data)
# write_csv()関数を用いて出力
write_csv(annual_stock_data, "../simulation_data/annual_stock_data.csv")
```
------------------------------------------------------------------------
## 統計的推論入門
### リターン・データを用いた統計的推論
::: {.callout-note icon="false"}
#### 目標
`firm_ID`が`1`の銘柄の月次超過リターン$R_{1,t}^e$は,期待値の意味でゼロより大きいだろうか?
:::
- すなわち,月次リターン$R_{1,t}$が期待値の意味で無リスク金利$R_{F,t}$より大きいかどうかを統計的に検定したい.
- 中心極限定理に基づくと,真の期待値がゼロという仮定の下で,以下で定義される\textcolor{blue}{\textbf{$t$値}} ($t$-value)は近似的に標準正規分布に従う($\stackrel{d}{\approx }$は「分布が近似できる」の意味). $$
\begin{align}
t=\frac{\bar{X}-\mu_0}{\sqrt{s^2/n}} \; \stackrel{d}{\approx } \; {\rm N}(0, 1) \label{eq:t-value} \tag{5.2}
\end{align}
$$ ここで,$\bar{X}$は標本平均,$s^2$は標本分散,$n$は標本サイズである.また,$\mu_0$は帰無仮説(後述)の値で,ここでは真の期待値と等しくゼロとする.$t$値は超過リターンに限らず一般的に定義されるため,ここではあえて$\bar{R}_1^e$でなく,$\bar{X}$という記法を採用している.$\mu_0=0$を省略しなかったのも同様の理由である.
------------------------------------------------------------------------
### 関数に頼らない$t$検定
- 以下のコードでは,まず`drop_na()`関数を利用して欠損値を除去した後の月次超過リターンのベクトルを`Re_firm_ID_1`として定義している.
- その後,(5.2)式を定義通りに計算すると,この場合の$t$値は約2.12であることが分かる.
```{r}
# 月次超過リターンの期待値に関するt検定 (1)
Re_firm_ID_1 <- stock_data %>%
filter(firm_ID == 1) %>% # firm_IDが1の企業のみ抽出
select(Re) %>% # 月次超過リターンのみ抽出
drop_na() %>% # 欠損値を削除
unlist() # データフレームからベクトルに変換
mu0 <- 0 # 帰無仮説を期待値0と設定
n <- length(Re_firm_ID_1) # 標本サイズ
t_value <- (mean(Re_firm_ID_1) - mu0) / sqrt(var(Re_firm_ID_1) / n) # 定義に従ってt値を計算
## [1] 2.121296
```
------------------------------------------------------------------------
### 既成の関数を使うやり方
- Rでは$t$検定を行うために`t.test()`関数が用意されている.
- この関数は第一引数に標本集合を取り,第二引数以降に検定の詳細を指定する.第二引数以降が省略された場合,自動的に帰無仮説は期待値ゼロに設定される.
```{r}
#| eval: false
# 月次超過リターンの期待値に関するt検定 (2)
t.test(Re_firm_ID_1) # t.test()関数で第二引数以降を省略
```
{width="80%"}