14 実習課題

佐久間 智広
sakuma@port.kobe-u.ac.jp

神戸大学大学院経営学研究科

2024/07/15


0.1 準備

0.1.1 パッケージの読み込み

Code 
1if (!require("pacman")) install.packages("pacman")
pacman::p_load(tidyverse,magrittr, ggpubr,
               estimatr,car,modelsummary,ggrepel,
               patchwork,broom,psych,datarium,
2               sjPlot,dae,AER,causaldata,wooldridge)
1
複数のパッケージを一度に読み込めるpacmanパッケージが入っていない場合は，インストールする
2
パッケージの読み込み
pacman

複数のパッケージを読み込めるパッケージ。そのパッケージの中のp_loadコマンドを使うと，（）内に指示したパッケージを読み込める。さらにそのパッケージがそもそもインストールされていない場合にはインストールした後に読み込んでくれる

tidyverse

Rのコードを楽にするたくさんのパッケージをパッケージにしたもの

magrittr

tidyverseに含まれる%>%などのコードをさらに拡張するもの。これがあると%$%とか%<>%が使える

1 前回の課題

1.1 問題（ハンバーガー統計学より引用）

ある小学校で、算数の分数の計算を教えるためのマンガを使った新しい教材を開発した。この教材の効果は従来のものと比べ、効果があるようだということはわかっているが、さらにその効果が子どもの算数に対する好みによってどう違うのかを調べたいと思う。

この効果を調べるために、あるクラスでは従来の教材で教え（統制群）、別のクラスではマンガ教材で教えた（マンガ群）。一日おいて、分数の計算テストをした。このとき、各クラスで、算数が好きか嫌いかというアンケートをあらかじめ取っておき、算数が好きな子ども10人と嫌いな子ども10人とで比較することにした。

テストの点数データ（10点満点）は次のようになった。これを分散分析したい。

統制群 マンガ群
算数が好き 7, 8, 6, 8, 10, 7, 8, 8, 9, 7 8, 9, 10, 10, 8, 8, 9, 7, 10, 8
算数が嫌い 4, 6, 5, 4, 3, 7, 5, 6, 4, 5 8, 7, 8, 6, 9, 7, 8, 8, 10, 8

(1)　この検定での帰無仮説を言いなさい。

(2)　この検定での対立仮説を言いなさい。

(3)　4つの条件におけるそれぞれの平均と標準偏差を計算しなさい。

(4)　分散分析を行いなさい。

(5)　有意水準を1%としたとき、この分散分析表から言えることを書きなさい。

(6)　以上の検定の結果を、わかりやすいことばで説明しなさい。

1.1.1 データ作成

Code 
score <- c(7, 8, 6, 8, 10, 7, 8, 8, 9, 7,
           8, 9, 10, 10, 8, 8, 9, 7, 10, 8,
           4, 6, 5, 4, 3, 7, 5, 6, 4, 5,
           8, 7, 8, 6, 9, 7, 8, 8, 10, 8)
like <- c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
          1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
          0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
          0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
manga <-c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
          1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
          0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
          1, 1, 1, 1, 1, 1, 1, 1, 1, 1)
kadai <- tibble(score,like,manga) %>% 
  mutate(like = factor(like, levels = c(1, 0), labels = c("like", "dislike")),
         manga = factor(manga, levels = c(1, 0), labels = c("manga", "normal")))

1.2 解答例

(1) この検定での帰無仮説を言いなさい

マンガ教材の効果は，算数の好き嫌いによって変わらない（差がない）

Note

問題文から，マンガ教材の効果自体はすでに明らかになっています。今回知りたいのはその効果が算数の好き嫌いによって変わるのかどうか（例えば，算数が元々嫌いな人ほどマンガ教材の効果が高い，など）です。帰無仮説は否定可能な形で設定する必要があるので「マンガ教材の効果は，算数の好き嫌いによって変わらない」になります。

(2) この検定での対立仮説を言いなさい。

マンガ教材の効果は，算数の好き嫌いによって変わる（差がある）

Important

「帰無仮説は否定可能な形で」という点について，考え方は中学？高校？で習う背理法と似ています。

  • 背理法では証明したい内容を否定するような形で仮説を立てます。そしてその仮説が矛盾することを示す→証明したい内容が正しい，みたいな論理で証明するものでした。
  • 統計的仮説検定でも似たように，証明したいこと（多くの場合AとBには差がある，とかAは0ではないとか）の否定（AとBには差がない（=差が0），とかAは0である）を帰無仮説としておきます。その帰無仮説が正しいとして，データの推定結果が得られる確率が十分に低い（p値が0.1以下とか，0.05以下とか）ときに，帰無仮説を棄却→証明したいことの方が正しそうだと判断する，という論法です。

(3)　4つの条件におけるそれぞれの平均と標準偏差を計算しなさい。

  1. 最もアナログな方法
Code 
#マンガ教材かつ算数好き
1kadai_manga_like <-kadai %>%
2  filter(manga == "manga") %>%
  filter(like == "like")  
mean(kadai_manga_like$score)
sd(kadai_manga_like$score)
1
マンガ教材かつ算数好きの人だけのデータを新たに作る
2
filter()関数は，()内の条件に当てはまるものだけを取り出す関数 
[1] 8.7
[1] 1.05935

これを各条件ごとに繰り返すと4条件それぞれの平均と標準偏差がわかる

  1. スマートな方法
Code 
kadai %>% 
1  group_by(manga, like) %>%
  summarise(mean(score), 
2            sd(score))
1
group_by()関数は，()内の変数（ダミー変数やカテゴリ変数）ごとに分ける関数。%>%で繋いだその後の処理をグループごとに行ってくれる
2
summarise()関数は，()内の処理を表形式でまとめる関数。group_byとセットで使われる（参考リンク）
  1. 表の形で出力する方法
Code 
datasummary(score  ~ manga * like * (mean + sd) ,
1            data = kadai)
1
modelsummaryパッケージのdatasummary()関数を使う。論文とかレポートにそのまま貼れる表が作れる。上級者向け。
manga normal
like dislike like dislike
mean sd mean sd mean sd mean sd
score 8.70 1.06 7.90 1.10 7.80 1.14 4.90 1.20

(4)　分散分析を行いなさい。

Code 
aov(score ~ like * manga, data = kadai) |>  
  summary()
            Df Sum Sq Mean Sq F value   Pr(>F)    
like         1  34.22   34.22  27.079 8.05e-06 ***
manga        1  38.03   38.03  30.086 3.39e-06 ***
like:manga   1  11.02   11.02   8.723  0.00551 ** 
Residuals   36  45.50    1.26                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(5)　有意水準を1%としたとき、この分散分析表から言えることを書きなさい。

例：likeとmangaの交互作用は，1%水準で統計的に有意。（likeとmangaそれぞれの単純な効果も1%水準で有意。これは今回知りたいこととは違うけど）

(6)　以上の検定の結果を、わかりやすいことばで説明しなさい。

例：マンガ教材の効果は，算数の好き嫌いによって変わらない（差がない）という帰無仮説は1%水準で棄却され，対立仮説を採択する。つまり，マンガ教材の効果は算数の好き嫌いによって変わると結論づけられる。

参考までにグラフも作成

Code 
ggline(data = kadai, #データを指定
       x = "manga", #x軸
       y = "score", #y軸
       color = "like", #色分けしたい条件
       add = c("mean") #それぞれの条件での平均値を載せる
       ) +
  theme_minimal()

  • 算数好きの人はどちらの教材でも点数が高いのであんまり差がない。
  • 一方で，算数嫌いの人は，マンガの教材を使ったグループの方が普通の教材グループよりもかなり高い平均点をとっている。

2 期末課題

2.1 概要

2.1.1 趣旨

  • 今回の課題は，これまで扱ってきた内容を包括的に扱います。
  • また，下記課題の1にある，データを見て明らかにする課題を自分で決めるという点は，この授業で主に扱った分析の知識や技法とは違うけれど，社会調査には必要な発想です。
  • 今回の課題の順にデータを扱い，分析をするのが社会調査の基本的な流れです。
    • 一連の流れがうまくできたら，（統計学や計量経済学，心理統計学が専門の先生のゼミに所属している方以外は）データを扱う分析を伴う卒業論文に必要なことはほとんどできていると言えそうです（ただし，アンケートなど，研究方法によって別の分析手法の知識を補足する必要がある）

2.1.2 提出方法と締め切り

  • 提出期限は立命館大学の春セメスター授業終了日である7月31日水曜日とします。
  • wordやpdf，html等ファイルの形で提出してください。 ファイル名は「課題_お名前」としてください。
  • ファイルの本文の冒頭に学籍番号とお名前を記載してください。
  • 問題は1から7まであります。どれについて取り組んでいるかわかるように作成してください
  • 最終授業は7月20日です。簡単なまとめの後，質問等があれば受け付けます。
    • ただし，できる限り「こうやってみたけどうまくいかない」等の質問にしてください。まだ何も手をつけていない状態で「何をすれば良いかわからない」というのはちょっと困ります。

Note

課題とデータの説明の後に（課題とは違うデータを使った）取り組み例を載せています。参考にされてください。

Note

なお，課題候補データの一部は特定のパッケージ内のデータです。授業資料冒頭のパッケージの読み込みコマンドを実行してから取り組んで下さい。

2.2 課題

今まで授業で扱ってきた内容を踏まえ，次ページ以降に示す5種類のデータのどれかを使ってデータ分析をしてもらいます。データを使って明らかにできそうな問いを考え，実際にデータを使って検証する，という一連の流れをやってもらうことを意図しています。

具体的にはデータの内容を確認した上で，以下の課題に取り組んでください。書式は自由ですが，コードと結果両方がわかるように一つのファイルにまとめてください(wordやpdfなどの形で報告書としてまとめてください)

  1. 明らかにするべき問い（疑問）を決めてください。問いの立て方は自由ですが，データを使って分析したら明らかにできるような問いを立ててください。
  2. 問いに対する予測（仮説）を考え，説明してください。(関連：第7回資料，それ以降の授業課題)
  3. データのどの変数をどのように分析するかを説明してください（使う変数と分析方法を明記してください）（関連：第8〜10，12回資料）
  4. データの中で，分析に用いる変数について，記述統計量（平均・標準偏差・最大値・最小値等）をまとめてください。（関連：第4回資料，それ以降の授業課題）
  5. 問いに関係する変数（もしくは複数の変数間の関係）を図示してください。(関連：第4回資料，第5回資料)
  6. 3. に書いた分析方法で分析し，その結果を解釈してください。
  7. 分析結果を踏まえて1. で設定した問いに対する答えを書いてください。

2.3 データ

2.3.1 データ1 : Determinants of Wages Data

Code 
data("CPS1988")
data1 <- CPS1988

US Census Bureau (日本の国勢調査に対応するようなことをしている組織)が1988年に行った質問票調査の結果です。

  • 7変数，28,155名分
  • 18 ~70歳 の男性で，1992年の年間収入が50ドル以上で，なおかつ自営業でも無給労働者でもない人が対象。
wage

週給（UDドル）

education

教育年数

experience

就業経験年数

ethnicity

人種(caucが白人，afamがアフリカ系アメリカ人)

smsa

アメリカ合衆国大都市統計地域に住んでいるかどうか

region

住んでいる地域（"northeast"北東部, "midwest"中西部, "south"南部, "west"西部）

parttime

パートタイマーかどうか

Tip

パッケージに組み込まれているデータなので，上記コードを実行するとデータを読み込めます。

2.3.2 データ2 : Titanic

タイタニック号の乗客の特性と生存に関するデータ

  • 2201名分，4変数
Code 
data2 <- titanic

data2 <- data2 |> 
  mutate(sex = factor(sex,  
                      levels = c(0,1), 
                      labels = c("Female", "Male")),
         class = factor(class,  
                      levels = c(1,2,3,4), 
                      labels = c("1st", "2nd", '3rd', 'Crew')),
         survived = factor(survived,  
                      levels = c(0,1), 
                      labels = c("No", "Yes")),
         age = factor(age,  
                      levels = c(0,1), 
                      labels = c("Child", "Adult")))
class

乗船クラス (ticket)

age

年齢 (Child vs. Adult)

sex

性別

survived

生き残ったかどうか

Tip

パッケージに組み込まれているデータなので，上記コードを実行するとデータを読み込めます。読み込んだ時点では，各変数の数値が何を表しているかわからないので，2行目以降でラベルを振っています。

2.3.3 データ3：attend

Professors Ronald Fisher と Carl Liedholm が，ミシガン州立大学 (Michigan State University) でミクロ経済学の授業を行った際に収集したデータ。

  • 11の変数，680名分
Code 
data3 <- attend

  • attend: 32回中何回授業に出席したか

  • termGPA: その期のGPA

  • priGPA: その期までのGPA

  • ACT: ACTのスコア （高校生が受ける標準テスト。センター試験にやや近い？）

  • final: 期末試験の点数

  • atndrte: 出席率

  • hwrte: 宿題提出率

  • frosh: 新入生は1を取るダミー変数

  • soph: 2回生は1を取るダミー変数

  • missed: 欠席回数

  • stndfnl: 期末テストのz値1 (final - mean)/sd

Tip

パッケージに組み込まれているデータなので，上記コードを実行するとデータを読み込めます。

2.3.4 データ4：housing

(14_housing.csvがmanabaにアップロードしてあります)

ニューヨーク州の不動産データ

  • Price: 価格

  • Living.Area: 広さ（平方フィート）

  • Bathrooms: バスルーム（ユニットバス等）の数

  • Bedrooms: 部屋数

  • Fireplaces: 暖炉の数

  • Age: 築年数

  • Fireplace: 暖炉があるかどうか（あるとき1）

2.3.5 データ5：rent

(14_rent.csvがmanabaにアップロードしてあります。)

千葉県市川市の家賃データ

（変数名が日本語なので説明省略）

2.4 実施例

以下では，課題1-7の実施例を挙げます。

（この通りに進めていただきたいというわけではなく，あくまでどんな感じで進めるかをイメージしやすくするためだけの例です。）

使うデータ

使うデータは，Cnet.com が集めた（米国？）市場に出回るタブレットPCの性能に関するデータです。

Code 
data <- read_csv("data/14_tablet.csv")
data

Model : モデル名

Battery life (hrs) ：電池の持ち(時間)

Max Brightness(cd/m2) ：最高照度(cd/m2)

Resolution ：画面縦横サイズ（ピクセル数）

Pixel density (ppi) ：ピクセル密度(ppi)

Screen size(in)：画面サイズ（インチ）

準備

1. 変数名を変える

変数名にスペースがあるのは望ましくないし，単位があるのも書きにくいので，変数の名前を変えます。

Code 
data <- data %>% 
  rename(battery = `Battery life (hrs)`,
         bright = `Max Brightness(cd/m2)`,
         pixel =`Pixel density (ppi)`,
         size = `Screen size(in)`)
2. 縦横比をカテゴリ変数に

縦横比は，×がついていて，数値データではなく文字データとして登録されています。画面サイズのバリエーションはいくつかに限られるので，カテゴリ変数とします。今回は特に（授業で扱っていない）順番付きのカテゴリ変数に変えてみています。

Code 
data <- data %>% 
  mutate(Resolution = factor(Resolution,ordered = TRUE))
data$Resolution
 [1] 1,024x768   1,280x800   1,920x1,200 2,560x1,600 2,048x1,536 2,048x1,536
 [7] 1,024x768   1,280x800   1,280x800   1,024x600   1,280x800   1,920x1,200
[13] 1,440x900   1,920x1,280 1,280x800   1,280x800   1,366x768   1,280x800  
[19] 1,920x1,200 2,560x1,600 1,024x600   1,280x800   1,920x1,200 1,280x800  
[25] 1,366x768   1,280x800   1,280x800   1,920x1,200 1,920x1,080 1,920x1,080
[31] 1,920x1,080 1,280x800   1,280x800   2,560x1,600 1,024x600   1,024x600  
[37] 1,280x800   1,280x800   1,280x800   1,920x1,200 1,024x600   2,560x1,600
[43] 1,280x800   2,560x1,600
10 Levels: 1,024x600 < 1,024x768 < 1,280x800 < 1,366x768 < ... < 2,560x1,600

2.4.1 明らかにするべき問い（疑問）を決めてください。問いの立て方は自由ですが，データを使って分析したら明らかにできるような問いを立ててください。


バッテリーの持ちは，画面の解像度が高くなったり，画面サイズが大きくなったりすると短くなるのか？つまり，バッテリーの持ちと画面の大きさや綺麗さはトレードオフの関係にあるのか？

2.4.2 問いに対する予測（仮説）を考え，説明してください。

画面の解像度が高くなると，たくさんの光の粒を発光させる必要があるそのため，バッテリーをたくさん食うことが考えられる。

仮説1

（他の画面の特性が一定ならば）画面の解像度とバッテリーの持ちは負の関係がある

画面のサイズが大きくなると，その分画面を表示させるのに必要な光の量が増える。結果としてバッテリーをたくさん食うかもしれない。一方で，画面のサイズが大きくなると，より大きなバッテリーを設置することが可能になる。そのため画面の大きいタブレットほど容量の大きなバッテリーを積んでいて，それゆえバッテリーが長持ちする（もしくは小さい画面と同等に長持ちする）可能性がある。どちらの予測も立つので，帰無仮説として以下のように仮説を設定する。

仮説2

（他の画面の特性が一定ならば）画面の大きさとバッテリーの持ちには関係がない

画面が明るければ明るいほど，よりたくさんのエネルギーを消費すると考えられる。結果としてバッテリーの持ちが悪くなることが考えられる。

仮説3

（他の画面の特性が一定ならば）画面の明るさとバッテリーの持ちは負の関係がある

解像度が高い画面は基本的にはより高性能であると考えられる。高性能な画面ほど明るさの性能も高い。高性能かつ明るい画面は，バッテリー性能も高いハイエンド商品で，バッテリーの持ちが良い可能性がある。

仮説4

解像度が高く，なおかつ明るい画面の場合，さらにバッテリーの持ちが良い。

Note

仮説は「説」なので，ただ仮説の文言を書くだけでなく，上のように各仮説が出てくるロジックを説明してください。

また，問いと違って仮説は統計的分析と対応している必要があります（つまりデータを何らかの方法で分析したら答えが出る形にする必要がある）

2.4.3 データのどの変数をどのように分析するかを説明してください（使う変数と分析方法を明記してください）

以下のような回帰分析によって仮説を検証する

\[ battery_i = \beta_0 + \beta_1 pixel_i + \beta_2 size_i + \beta_3 bright_i + \beta_4 bright_i \times pixel_i + \varepsilon_i \]

iは，各サンプル（各機種）を表す。ここで，

  • 仮説1は，\(\beta_1\)の推定値が負であることを，
  • 仮説2は，\(\beta_2\)の推定値が正または負であることを，
  • 仮説3は，\(\beta_3\)の推定値が負であることを，
  • 仮説4は，\(\beta_4\)の推定値が正であることを

それぞれ予測している。

有意水準を10%として仮説を検証する。

2.4.4 データの中で，分析に用いる変数について，記述統計量（平均・標準偏差・最大値・最小値等）をまとめてください。

Code 
data %>% 
  select(battery, pixel, size, bright) %>% 
  datasummary_skim()
Unique Missing Pct. Mean SD Min Median Max Histogram
battery 31 16 8.9 2.3 4.6 8.4 14.2
pixel 29 0 213.3 56.2 135.0 212.0 339.0
size 11 0 8.8 1.5 7.0 8.9 11.6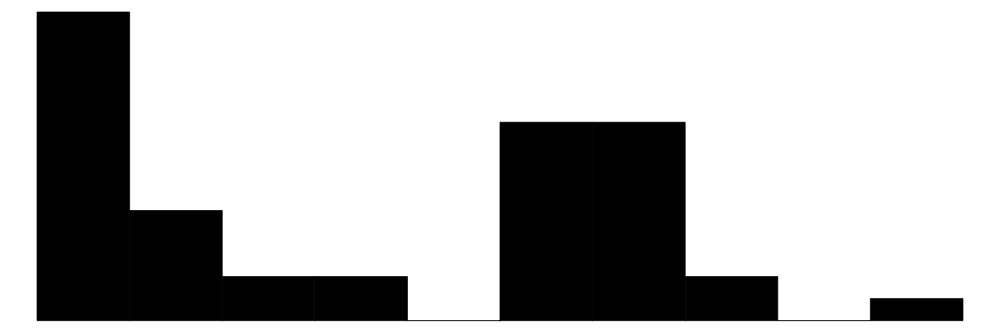
bright 36 7 386.7 91.1 232.0 379.0 676.0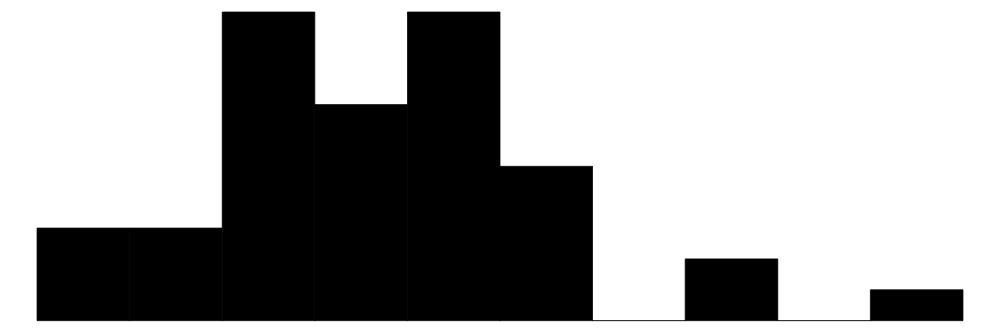

バッテリー持続時間の平均は8.9時間，解像度の平均は213.3ppi。サイズに関しては右のヒストグラムから，大きく二分化していることが見てとれる。

回帰分析により変数間の関係を見るので，相関行列も見ておく

Code 
data %>% 
  select(battery, pixel, size, bright) %>% 
  datasummary_correlation()
battery pixel size bright
battery 1 . . .
pixel .02 1 . .
size .18 -.07 1 .
bright .34 .19 -.01 1

sizeとbattery, brightとbatteryにそれぞれ正の相関が見て取れる。サイズが大きいものほどバッテリーの持ちがよく，明るいものほどバッテリーの持ちが良い。また，明るさとピクセルには正の相関がある。性能の良いディスプレーはピクセル数が多い（解像度が高い）かつ明るいということかもしれない。

2.4.5 問いに関係する変数（もしくは複数の変数間の関係）を図示してください。

すでにヒストグラムは記述統計の端っこについていたので，各変数間の散布図を一度に作る。

Code 
data %>% 
  select(battery, pixel, size, bright) %>% 
  plot()

解釈は相関表と同じ

2.4.6 3. に書いた分析方法で分析し，その結果を解釈してください。

Code 
result <- lm_robust(battery ~ pixel + size + bright + bright*pixel, data = data)
summary(result)

Call:
lm_robust(formula = battery ~ pixel + size + bright + bright * 
    pixel, data = data)

Standard error type:  HC2 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)   CI Lower  CI Upper DF
(Intercept)  10.9830872  4.923e+00   2.231  0.03357  9.152e-01 2.105e+01 29
pixel        -0.0469043  2.360e-02  -1.988  0.05635 -9.516e-02 1.356e-03 29
size          0.4468475  2.472e-01   1.807  0.08110 -5.882e-02 9.525e-01 29
bright       -0.0152618  1.369e-02  -1.115  0.27409 -4.326e-02 1.274e-02 29
pixel:bright  0.0001189  5.643e-05   2.108  0.04380  3.539e-06 2.343e-04 29

Multiple R-squared:  0.2633 ,   Adjusted R-squared:  0.1617 
F-statistic: 5.765 on 4 and 29 DF,  p-value: 0.001535

分析の結果，

  • 仮説1に関して，pixelの係数\(\beta_1\)の推定値が有意に負(p = 0.056)であった。ピクセルが1上がるとバッテリーの持ちが0.04時間短くなることを意味する。仮説1を支持する結果だった。

  • 仮説2に関して，sizeの係数は有意に正（p = 0.081）だった。サイズ1インチ上がるたびに電池の持ちが0.45時間長くなる。

  • 仮説3に関して，brightの係数は有意ではなかった。明るさと電池の持ちの良さに関係がないという帰無仮説を棄却できなかったことを意味する。仮説3は支持されなかった。

  • 仮説4に関して，pixel × brightの係数は有意に正（p = 0.044）だった。ピクセル数が多いかつ明るいディスプレイを持つタブレットの電池の持ちは良いことを意味し，仮説4を支持する。

  • ただし，自由度調整済み\(R^2\)は0.16と高くないため，今回扱ったディスプレイ性能ではバッテリー持続時間の差の一部しか説明できない。

Note

上のように，推定結果が何を意味しているか，それが事前に設定した仮説を支持したのか，それとも否定したのかについて記載してください。

2.4.7 分析結果を踏まえて1. で設定した問いに対する答えを書いてください。

当初の問いは

バッテリーの持ちは，画面の解像度が高くなったり，画面サイズが大きくなったりすると短くなるのか？つまり，バッテリーの持ちと画面の大きさや綺麗さはトレードオフの関係にあるのか？

だった。仮説1から4を検証した結果，この問いに対する答えは以下のようにまとめられる。

バッテリーの持ちは，解像度や画面サイズといった一見電力をたくさん消費しそうな特徴があるほど短くなる，という単純な関係にあるわけではなかった。解像度に関しては，高くなるほどバッテリーの持ちが短い傾向が見て撮れたが，サイズは大きくなるほどバッテリーの持ちが良い。後者に関しては，画面サイズが大きいほど本体が大きくなり，大きなバッテリーを搭載できるからだと考えられる。また，解像度が高く，なおかつ明るいような高性能のディスプレイを持つタブレットは，ハイエンド商品であることが予測され，それゆえバッテリー性能も高いようであった。

2024社会調査法（立命館大学）