参考:統計・データ分析の本
統計やデータ分析は,簡単ではありません。
確率論,計量経済学それぞれちゃんと勉強するのは難しいです。
大学院レベルの授業それぞれ15回分ずつ使うような内容です。
そのあと実際の分析手法についての授業,など
この授業でも,統計の仕組みについてはほんのさわりの触りぐらいしか扱っていません。
実際に分析できるように,という方を重視しています。
もし,ご自身でもっと勉強したいという方のためにいくつか本を紹介します。
とっかかりとして
統計・データサイエンスの役割について,事例を見ながら知りたい
伊藤公一朗(2017)データ分析の力: 因果関係に迫る思考法
中室牧子・津川友介(2017)原因と結果の経済学: データから真実を見抜く思考法
データ分析されたものを読めるようになりたい
森田果(2014)実証分析入門 データから「因果関係」を読み解く作法
山本勲(2015)実証分析のための計量経済学: 正しい手法と結果の読み方
勉強し始めるなら…
田中隆一(2015)計量経済学の第一歩:実証分析のススメ
星野匡郎・田中久稔・北川梨津 (2023) Rによる実証分析 : 回帰分析から因果分析へ. 第2版.
今井耕介(2018)社会科学のためのデータ分析入門 上・下
Jeffrey M. Wooldridge (2019) Introductory Econometrics: A Modern Approach
めっちゃちゃんと勉強するなら (大学院入門レベル)
DeGroot, M.H., and M.J. Schervish (2022訳書)確率と統計
Stock, J.H., and M.W., Watson (2016訳書)入門 計量経済学
準備
パッケージの読み込み
Code
1 rm (list= ls ()); gc (); gc ();if (! require ("pacman" )) install.packages ("pacman" ):: p_load (magrittr,2 conflicts_prefer (dplyr:: select ())
1
複数のパッケージを一度に読み込めるpacmanパッケージが入っていない場合は,インストールする
2
パッケージの読み込み
pacman
複数のパッケージを読み込めるパッケージ。そのパッケージの中のp_loadコマンドを使うと,()内に指示したパッケージを読み込める。さらにそのパッケージがそもそもインストールされていない場合にはインストールした後に読み込んでくれる
tidyverse
Rのコードを楽にするたくさんのパッケージをパッケージにしたもの
magrittr
tidyverseに含まれる%>%などのコードをさらに拡張するもの。これがあると%$%とか%<>%が使える
概要
これまでの話
独立変数が複数ある時の重回帰分析
重回帰分析では、推定された各独立変数の係数は「その他の要因を一定とした」上での独立変数と従属変数の関係を検証できる
独立変数Aと関係のある要因Bを含めることは、推定の歪みや、擬似相関の問題を防ぐ意味でも重要
「ラーメンの評価を決めるのはスープ」
単回帰分析をして,スープの係数\(\beta_1\) が正で,なおかつ統計的に有意か確認
\[
\text{ラーメン評価} = \beta_0 + \beta_1 スープ + \varepsilon
\]
でも…麺も大事だしチャーシューも大事じゃない?
重回帰分析をすることで,\(\beta_1\) は「麺とチャーシューに対する評価を一定とした上でのスープの評価とラーメン評価の関係」になる
\[
ラーメン評価 = \beta_0 + \beta_1 スープ + \beta_2 麺 + \beta_3 チャーシュー + \varepsilon
\]
今日の話
特別な種類の変数(ダミー変数)とそれを含めた回帰分析
独立変数間の交互作用を考慮した回帰分析
変数を対数化した上での回帰分析
非直線回帰
これらは回帰分析でよく使われる手法で、分析の幅が広がるという意味でも入門的かつ重要なものです。
ダミー変数
ダミー変数とは
名義尺度(復習)
第4回に出てきた変数の種類を思い出してください
様々な計算ができる比例尺度(例えば企業の売上や家計の収入)とは違い、名義尺度には数量的な意味はない。
(男性0、女性1という数字を割り当てた)性別変数は、足し算も引き算も掛け算も意味がない
回帰に含めるダミーの変数
しかし、このような尺度も、ダミー変数(偽の変数?)として回帰分析に含めることが可能。
\[
income = \beta_0 + \beta_1 age + \beta_2 gender + u
\]
\(income\) は年収(円)、 \(age\) は年齢(歳)、 \(gender\) は性別(男は0女は1)とします。この回帰モデルを推定した場合、 \(\beta_1\) の推定値は「年齢が1歳上がると年収が \(\beta_1\) 円上がる」ということを示します。一方で、 「性別が1上がると年収が \(\beta_2\) 円上がる」とは言えません。なぜなら性別に関して便宜的に数字を振っているだけで、数字それ自体には意味がないからです。このような便宜的に振った数字をダミー変数と言います。ダミー変数は0か1で属性をに分割しています。そのため,以下のように,男性と女性で違う式が推定されます。
\[
\begin{cases}
income = \beta_0 + \beta_1 age + u & gender = 0 \text{(男性)} \\
income = \beta_0 + \beta_1 age + \beta_2 + u & gender = 1 \text{(女性)}
\end{cases}
\]
\[
\begin{cases}
income = \beta_0 + \beta_1 age + u & gender = 0 \text{(男性)} \\
income = \beta_0 + \beta_1 age + \beta_2 + u & gender = 1 \text{(女性)}
\end{cases}
\]
式からわかるように,男女で切片が変わることが想定され,男女別に2本の式が推定されていることになります。
このようにダミー変数を使うと,名義尺度や順序尺度のような数字として意味のない尺度で集計される情報を回帰分析に取り込むことができます。
例
11_temperature_aug.csvは,時間単位で測った電力使用量のデータです (星野, 田中, and 北川 2023 )
date
日付
time
時間(24時間表示)
elec
電力使用量(万kw)
prec
1時間あたり降水量(mm)
temp
東京都の気温(℃)
Code
<- read_csv ("data/11_temperature_aug.csv" )
Code
|> select (- date, - time) |> describe ()
日付や時間以外の変数の記述統計です。
例えば電気使用量の平均は3398万kw,降水量は平均0.14mm,平均気温は27℃などがわかります。
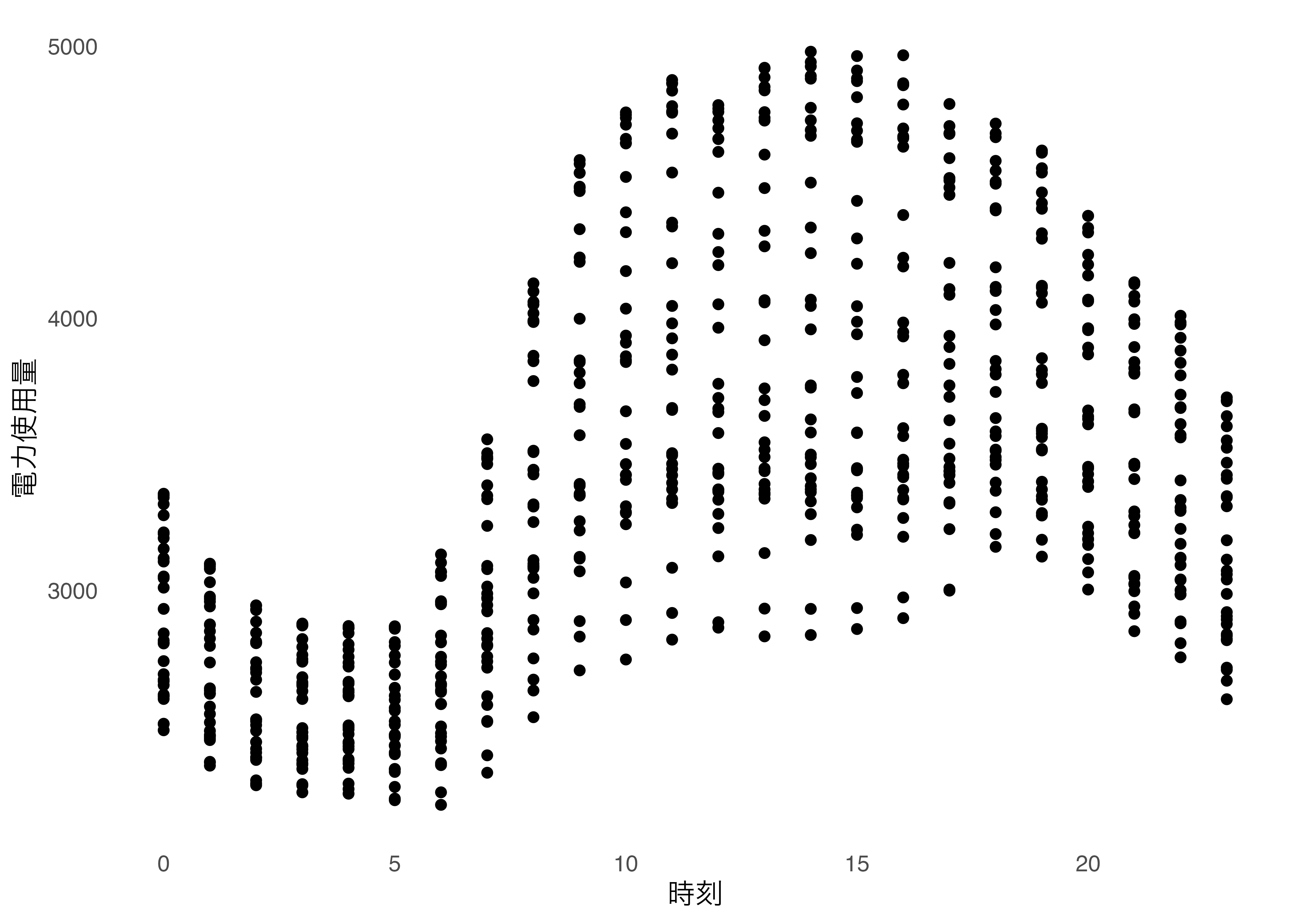
電力使用量と時間の関係を見てみるため,まず散布図を書いてみます
Code
|> ggplot (aes (x = time, y = elec)) + geom_point () + xlab ("時刻" ) + ylab ("電力使用量" ) + theme_minimal () + theme (panel.grid = element_blank ())
なんとなく日中の使用量が多い
そこで,日中の時間帯を午前,午後に分けて新しい変数を作ります。
Code
%<>% 1 mutate (morning = 1 * (6 <= time & time <= 12 ),2 afternoon = 1 * (13 <= time & time <= 18 ))
1
timeが6時から12時の時に1,それ以外で0となるmorningを作成
2
timeが13時から18時に1,それ以外で0となるafternoonを作成
変数と時間の関係
morning
1
0
0
afternoon
0
1
0
これらを電力使用量に回帰すると
\[
elec_i = \beta_0 + \beta_1 morning_i + \beta_2 afternoon_i + u_i
\]
Code
lm (elec ~ morning + afternoon, data = tem_aug) |> print ()
Call:
lm(formula = elec ~ morning + afternoon, data = tem_aug)
Coefficients:
(Intercept) morning afternoon
3043.7 457.7 885.2
ここでのmorning, afternoonそれぞれの解釈は
夜間と比べてmorningの時間帯は,電力使用量が平均的に457万kw多い
夜間と比べてafternoonの時間帯は,電力使用量が平均的に885万kw多い
\[
\begin{cases}
elec_i = \hat\beta_0 & \text{夜間}: morning == 0 & afternoon == 0 \\
elec_i = \hat\beta_0 + \hat\beta_1 & \text{午前}: morning == 1 & afternoon == 0 \\
elec_i = \hat\beta_0 + \hat\beta_2 & \text{午後}: morning == 0 & afternoon == 1 \\
\end{cases}
\]
Code
lm (elec ~ morning + afternoon, data = tem_aug) |> summary ()
Call:
lm(formula = elec ~ morning + afternoon, data = tem_aug)
Residuals:
Min 1Q Median 3Q Max
-1288.3 -489.9 -129.3 468.9 1573.3
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3043.69 33.38 91.176 <2e-16 ***
morning 457.65 53.53 8.549 <2e-16 ***
afternoon 885.25 56.19 15.754 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 616.4 on 741 degrees of freedom
Multiple R-squared: 0.2573, Adjusted R-squared: 0.2553
F-statistic: 128.4 on 2 and 741 DF, p-value: < 2.2e-16
ここで,新しく日付情報から変数を作る
土曜日(saturday)と日曜日(sunday)の変数を作る。
また,お盆休みの変数(recess)を作る。期間は2014/8/11から8/16まで
Code
%<>% 1 mutate (date = ymd (date),2 dow = wday (date,label = TRUE ))%<>% 3 mutate (saturday = 1 * (dow == "Sat" ),sunday = 1 * (dow == "Sun" ), 4 recess = 1 * ("2014-08-11" <= date & date <= "2014-08-16" ))
1
ymd()関数で,文字データとして読み込まれたdate変数を日付データに変換
2
wday()関数で,date変数から曜日を抽出して,曜日変数dowを作成
3
dowが土曜,日曜を識別するダミー変数(それぞれsaturday, sunday)を作成
4
お盆休みを識別するrecess変数を作成
Code
<- lm (elec ~ temp + prec + sunday + recess + morning + afternoon + saturday, data = tem_aug)summary (reg4_1)
Call:
lm(formula = elec ~ temp + prec + sunday + recess + morning +
afternoon + saturday, data = tem_aug)
Residuals:
Min 1Q Median 3Q Max
-900.25 -282.76 19.38 287.56 932.70
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 88.889 119.530 0.744 0.457
temp 119.712 4.357 27.474 < 2e-16 ***
prec 25.199 15.336 1.643 0.101
sunday -497.751 40.695 -12.231 < 2e-16 ***
recess -446.610 36.748 -12.153 < 2e-16 ***
morning 201.870 34.800 5.801 9.79e-09 ***
afternoon 571.845 37.087 15.419 < 2e-16 ***
saturday -256.122 39.716 -6.449 2.04e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 386.3 on 736 degrees of freedom
Multiple R-squared: 0.7104, Adjusted R-squared: 0.7076
F-statistic: 257.9 on 7 and 736 DF, p-value: < 2.2e-16
気温,午前(深夜と比べて),午後(深夜と比べて)は,有意に正の関係
日曜,土曜は(平日に比べて)有意に負の関係
お盆休みであることは(他の時期に比べて)有意に負の関係
Code
<- lm (elec ~ temp, data = tem_aug)<- lm (elec ~ temp + prec, data = tem_aug)<- lm (elec ~ temp + prec + sunday + saturday, data = tem_aug)<- lm (elec ~ temp + prec + sunday + saturday + recess, data = tem_aug)<- lm (elec ~ temp + prec + sunday + saturday + recess + morning + afternoon, data = tem_aug)list (reg4_1, reg4_2, reg4_3, reg4_4, reg4_5) |> msummary (gof_omit = "Log.Lik.|AIC|BIC|RMSE" , stars = TRUE )
(1)
(2)
(3)
(4)
(5)
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept)
-614.272***
-646.492***
-413.385**
-284.530*
88.889
(143.223)
(145.367)
(142.999)
(133.997)
(119.530)
temp
145.030***
146.068***
140.986***
140.151***
119.712***
(5.134)
(5.196)
(5.035)
(4.699)
(4.357)
prec
24.898
41.142*
46.319**
25.199
(19.493)
(18.800)
(17.550)
(15.336)
sunday
-374.277***
-482.532***
-497.751***
(48.856)
(46.735)
(40.695)
saturday
-213.387***
-232.276***
-256.122***
(48.814)
(45.585)
(39.716)
recess
-444.282***
-446.610***
(42.223)
(36.748)
morning
201.870***
(34.800)
afternoon
571.845***
(37.087)
Num.Obs.
744
744
744
744
744
R2
0.518
0.519
0.559
0.617
0.710
R2 Adj.
0.517
0.518
0.557
0.614
0.708
F
797.860
400.085
234.230
237.348
257.871
交互作用
重回帰分析では,複数の独立変数が含められますが,それらの変数間の関係を明示的に含めることも可能です。
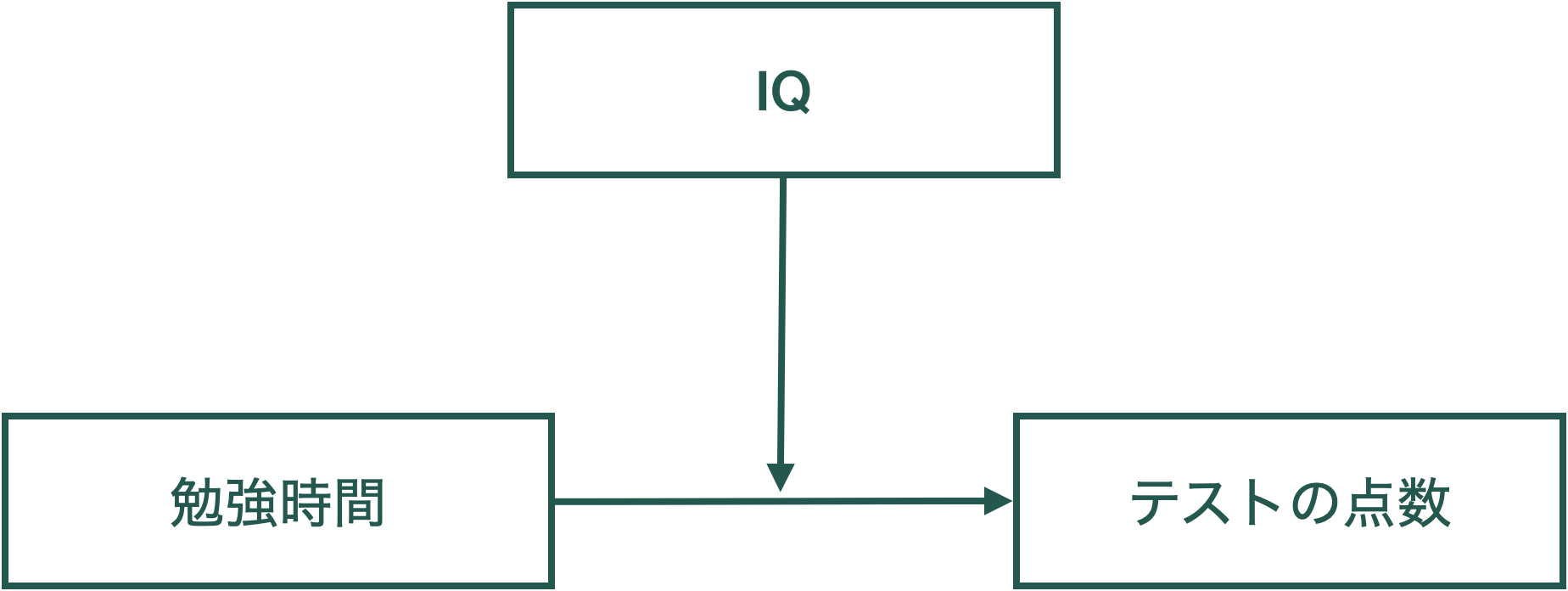
例1:テストの点数と勉強時間,IQ
ある学力テストについて,勉強時間との関係を推定します。
各受験者の学力テストの点数(test)と勉強時間(time),IQテストのスコア(IQ)が測定されていたとします。
ここで,分析者は「勉強時間がテストの点数に結びつく度合いは,IQによって違う」ことを予測しています。
\[
test_i = \beta_0 + \beta_1 time_i + \beta_2 IQ_i +\beta_3 time_i \times IQ_i + u_i
\]
\(\beta_3\) の項目は,時間とIQの掛け合わせになっています。これによって,テストの点数の時間に対する効果(の一部)は,IQに依存する,という関係が式に含まれることになります。
Code
<- read_csv ('data/11_timeiq.csv' )
time
勉強時間
IQ
IQテストのスコア
exam
テストの点(990点満点)
分析の際には,交互作用を検証したい独立変数間を「*」で繋いで書きます
lm(従属変数 ~ 独立変数1*独立変数2, data = データ名)
Code
lm (exam ~ time * IQ, data = timeiq) |> print ()
Call:
lm(formula = exam ~ time * IQ, data = timeiq)
Coefficients:
(Intercept) time IQ time:IQ
-55.93623 8.10315 3.69310 0.02524
ここから,
\[
exam = -55.9 + 8.10time+3.69IQ+0.02time\times IQ
\]
テストの点は,
で説明される
Code
<- lm (exam ~ time, data = timeiq)<- lm (exam ~ IQ, data = timeiq)<- lm (exam ~ time + IQ, data = timeiq)<- lm (exam ~ time * IQ, data = timeiq)list (r1, r2, r3, r4) |> msummary (gof_omit = "Log.Lik.|AIC|BIC|RMSE" , stars = TRUE )
(1)
(2)
(3)
(4)
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept)
290.791***
73.668
-166.666***
-55.936*
(8.975)
(53.111)
(6.662)
(24.970)
time
11.511***
10.704***
8.103***
(0.203)
(0.059)
(0.569)
IQ
6.879***
4.773***
3.693***
(0.513)
(0.064)
(0.243)
time × IQ
0.025***
(0.005)
Num.Obs.
500
500
500
500
R2
0.865
0.265
0.989
0.989
R2 Adj.
0.865
0.264
0.989
0.989
F
3201.821
179.930
22196.314
15403.316
例2:ダミー変数との交互作用
先ほど扱ったダミー変数と組み合わせるともう少しわかりやすくなります。
\[
income_i = \beta_0 + \beta_1 age_i + \beta_2 gender_i + \beta_3 age_i \times gender_i + u_i
\]
ただし,\(gender\) は,女性の場合に1,それ以外0のダミー変数です。この場合,genderは男女0,1しかないので
\[
\begin{cases}
income_i = \beta_0 + \beta_1 age_i + u_i & gender_i = 0 (女性以外) \\
income_i = (\beta_0 + \beta_2) + (\beta_1 + \beta_3) age_i + u_i & gender_i = 1 (女性)
\end{cases}
\]
となります。切片だけでなく,傾きも性別によって変わる,という仮定が置かれた分析になります。
変数を対数化した上での回帰分析
変数が正で,なおかつ大きな数字の時,変数を対数化する( \(\log_e\) の形にする)ことで,解釈がしやすかったり,よりデータにフィットした分析ができたりします。
特に, \(\log_e\) の形に変換することで,係数を弾力性として解釈できます。
つまり,解釈の際の単位を%とできます。
例:企業の株価と経営者の報酬
11_wage.csvはIQと年収が含まれた個人データです (Wooldridge 2013 )
Code
<- read_csv ('data/11_wage.csv' )
wage.csvに入っている変数のうち IQはその人のIQ, wageは月収です。また,lIQはIQの対数( \(\log _e IQ\) ), lwageは wageの対数 (\(\log _e wage\) )です。
wageとIQ
普通に回帰すると,IQの係数の解釈は,「IQが1高い時,年収が〇〇ドル高くなる」です。
Code
<- lm (wage ~ IQ, data = wage)summary (w1)
Call:
lm(formula = wage ~ IQ, data = wage)
Residuals:
Min 1Q Median 3Q Max
-898.7 -256.5 -47.3 201.1 2072.6
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 116.9916 85.6415 1.366 0.172
IQ 8.3031 0.8364 9.927 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 384.8 on 933 degrees of freedom
Multiple R-squared: 0.09554, Adjusted R-squared: 0.09457
F-statistic: 98.55 on 1 and 933 DF, p-value: < 2.2e-16
lwageとlIQ
対数化したもの同士を回帰すると,「IQが1%高い時,年収が〇〇%高くなる」という解釈になります
Code
<- lm (lwage ~ lIQ, data = wage)summary (w2)
Call:
lm(formula = lwage ~ lIQ, data = wage)
Residuals:
Min 1Q Median 3Q Max
-2.09743 -0.24828 0.02547 0.27542 1.21110
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.94218 0.38409 7.660 4.64e-14 ***
lIQ 0.83299 0.08334 9.995 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4005 on 933 degrees of freedom
Multiple R-squared: 0.09672, Adjusted R-squared: 0.09576
F-statistic: 99.91 on 1 and 933 DF, p-value: < 2.2e-16
lwageとIQ
従属変数や独立変数のどちらかだけを対数として回帰することもあります。wageだけを対数として回帰する場合「IQが1高い時,年収が〇〇%高くなる」です
Code
<- lm (lwage ~ IQ, data = wage)summary (w3)
Call:
lm(formula = lwage ~ IQ, data = wage)
Residuals:
Min 1Q Median 3Q Max
-2.09323 -0.25547 0.02261 0.27544 1.21487
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.8869942 0.0890206 66.13 <2e-16 ***
IQ 0.0088072 0.0008694 10.13 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3999 on 933 degrees of freedom
Multiple R-squared: 0.09909, Adjusted R-squared: 0.09813
F-statistic: 102.6 on 1 and 933 DF, p-value: < 2.2e-16
Code
<- lm (wage ~ lIQ, data = wage)list ("両方普通" = w1,"両方対数" = w2,"従属対数" = w3,"独立対数" = w4) |> msummary (gof_omit = "Log.Lik.|AIC|BIC|RMSE|F" , stars = TRUE )
両方普通
両方対数
従属対数
独立対数
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept)
116.992
2.942***
5.887***
-2628.053***
(85.642)
(0.384)
(0.089)
(369.814)
IQ
8.303***
0.009***
(0.836)
(0.001)
lIQ
0.833***
778.537***
(0.083)
(80.242)
Num.Obs.
935
935
935
935
R2
0.096
0.097
0.099
0.092
R2 Adj.
0.095
0.096
0.098
0.091
非直線回帰
回帰分析では,独立変数の2次関数を推定することを通して,直線ではない関係を推定することもできます。
例: MLB選手の給料
11_mlb.csvは過去のアメリカメジャーリーグの成績と給料のデータです(Wooldridge 2013 ) 。変数の説明のリンク
プレー年数 (years)と給料 (salary)を回帰すると,以下のようになります。
Code
<- read_csv ('data/11_mlb.csv' )lm (salary ~ years, data = mlb) |> summary ()
Call:
lm(formula = salary ~ years, data = mlb)
Residuals:
Min 1Q Median 3Q Max
-2971888 -665744 -382887 545184 4737399
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 248601 126132 1.971 0.0495 *
years 173429 17003 10.200 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1238000 on 351 degrees of freedom
Multiple R-squared: 0.2286, Adjusted R-squared: 0.2264
F-statistic: 104 on 1 and 351 DF, p-value: < 2.2e-16
年数と給料は有意かつ正の関係 (p < 0.001)。具体的には,年数が1年増えると,給料が173429ドル増えることが期待される。
しかし,年齢と給料は本当に直線関係でしょうか?野球選手の選手としてのピークは30歳前後で,多くが40歳までには引退します。引退前は成績も下がり,給料も最盛期よりも下がることが予想されます。つまり,年齢と給料の関係は(年功序列の)右肩上がりではなく,逆U字であると想定できます。
これを反映させるには,
\[
salary_i = \beta_0 + \beta_1 years_i + \beta_2 years^2_i + u_i
\]
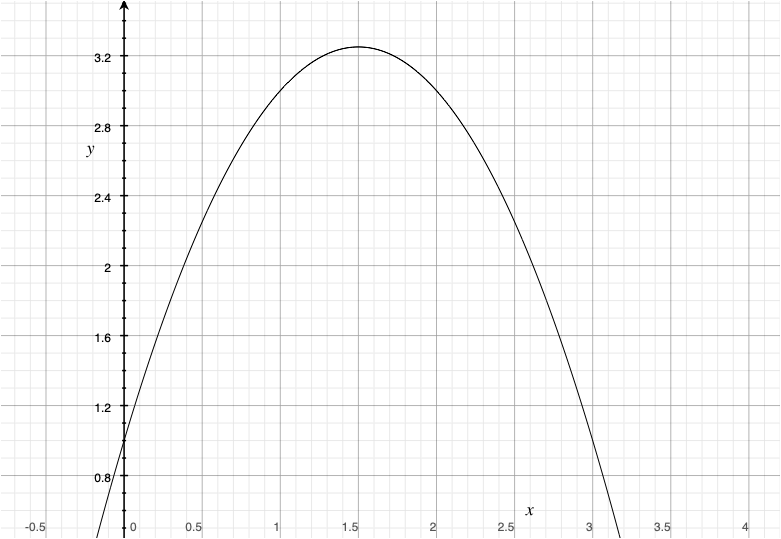
のような式を推定します。逆U時になるということは,給料は,プレー年数の二次関数で,なおかつ2乗の項がマイナス( \(\beta_2 <0\) )ということになるはずです。
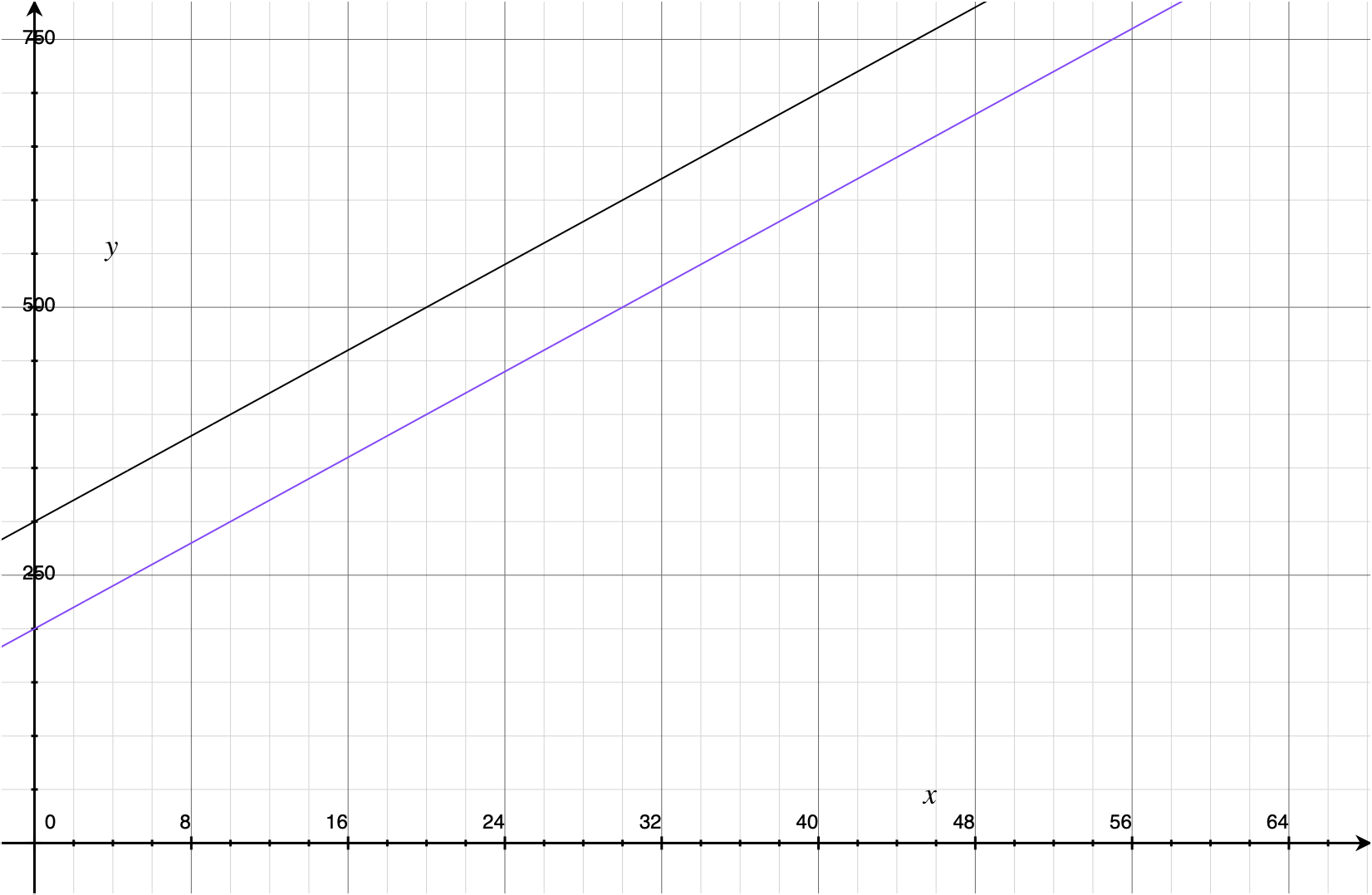
イメージ
Rでは,高次の項を含めるときには以下のように表現する
Code
lm (salary ~ years + I (years^ 2 ), data = mlb) %>% summary ()
Call:
lm(formula = salary ~ years + I(years^2), data = mlb)
Residuals:
Min 1Q Median 3Q Max
-2222264 -738297 -172264 546249 4466972
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -484233 190920 -2.536 0.0116 *
years 429943 53960 7.968 2.30e-14 ***
I(years^2) -16170 3240 -4.991 9.47e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1198000 on 350 degrees of freedom
Multiple R-squared: 0.2799, Adjusted R-squared: 0.2758
F-statistic: 68.02 on 2 and 350 DF, p-value: < 2.2e-16
実際分析すると, \(\beta_2\) の推定値は有意に負です。
このように,理論・論理上従属変数と独立変数との間の関係が直線関係ではないことが想定される場合,2乗項や3乗項を使って多次元の関数として推定することができます。
Code
list ("model1" = lm (salary ~ years, data = mlb),"model2" = lm (salary ~ years + I (years^ 2 ), data = mlb)|> msummary (gof_omit = "Log.Lik.|AIC|BIC|RMSE|F" , stars = TRUE ,title = "2乗を入れるか入れないか" )
2乗を入れるか入れないか
model1
model2
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept)
248601.059*
-484233.233*
(126132.314)
(190919.603)
years
173428.630***
429942.733***
(17003.299)
(53960.197)
I(years^2)
-16170.167***
(3239.590)
Num.Obs.
353
353
R2
0.229
0.280
R2 Adj.
0.226
0.276
2乗の項は統計的に有意。
モデルの当てはまり (\(R^2\) )も良くなっている
まとめ
重回帰分析の応用パターンについて幾つか紹介しました。
カテゴリ変数であるダミー変数を含める
独立変数間の交互作用を含める
独立変数を二次関数以上とする
様々な拡張をすることで,分析の幅が広がります。
参考
交互作用の例としてあげた以下の式について,
\[
test_i = \beta_0 + \beta_1 time_i + \beta_2 IQ_i +\beta_3 time_i \times IQ_i + u_i
\]
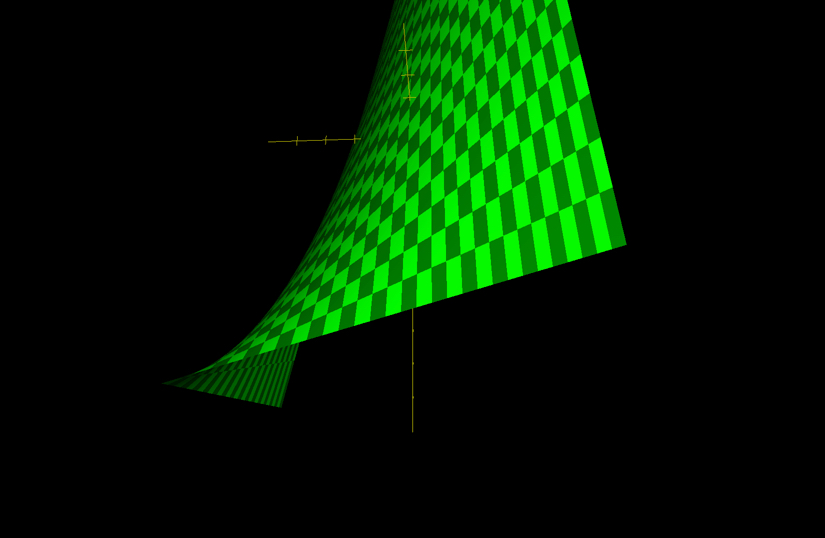
\(\beta_3\) の項目は,時間とIQの掛け合わせになっています。これによって,テストの点数の時間に対する効果(の一部)は,IQに依存する,という関係が式に含まれることになります。この式について推定式をtimeで微分すると以下のようになり,timeのtestに対する効果がIQに依存していることが分かります。また,図で表すと,次のような3次元の関係になります(交互作用が+の時の例)。
\[
\frac{\partial test}{\partial time}=\beta_1 + \beta_3 IQ
\]