12 公表データを用いた分析
2025/07/04
1 はじめに
前回は
- 企業の内部データ（をイメージしたもの）を使って，
- 企業内部者の視点で，
コスト構造を理解し，意思決定やコストマネジメントに役立てるためのコスト構造の推定を扱いました。
今回は，
- 公表データを使って
- 企業内部者の視点，及び企業外部者の視点から，
企業のコスト構造を推定し，それを通して投資の判断や政策判断に役立てよう，というイメージです。
具体的には公表財務諸表データを使ったコストビヘイビア分析を扱います。
1.1 準備
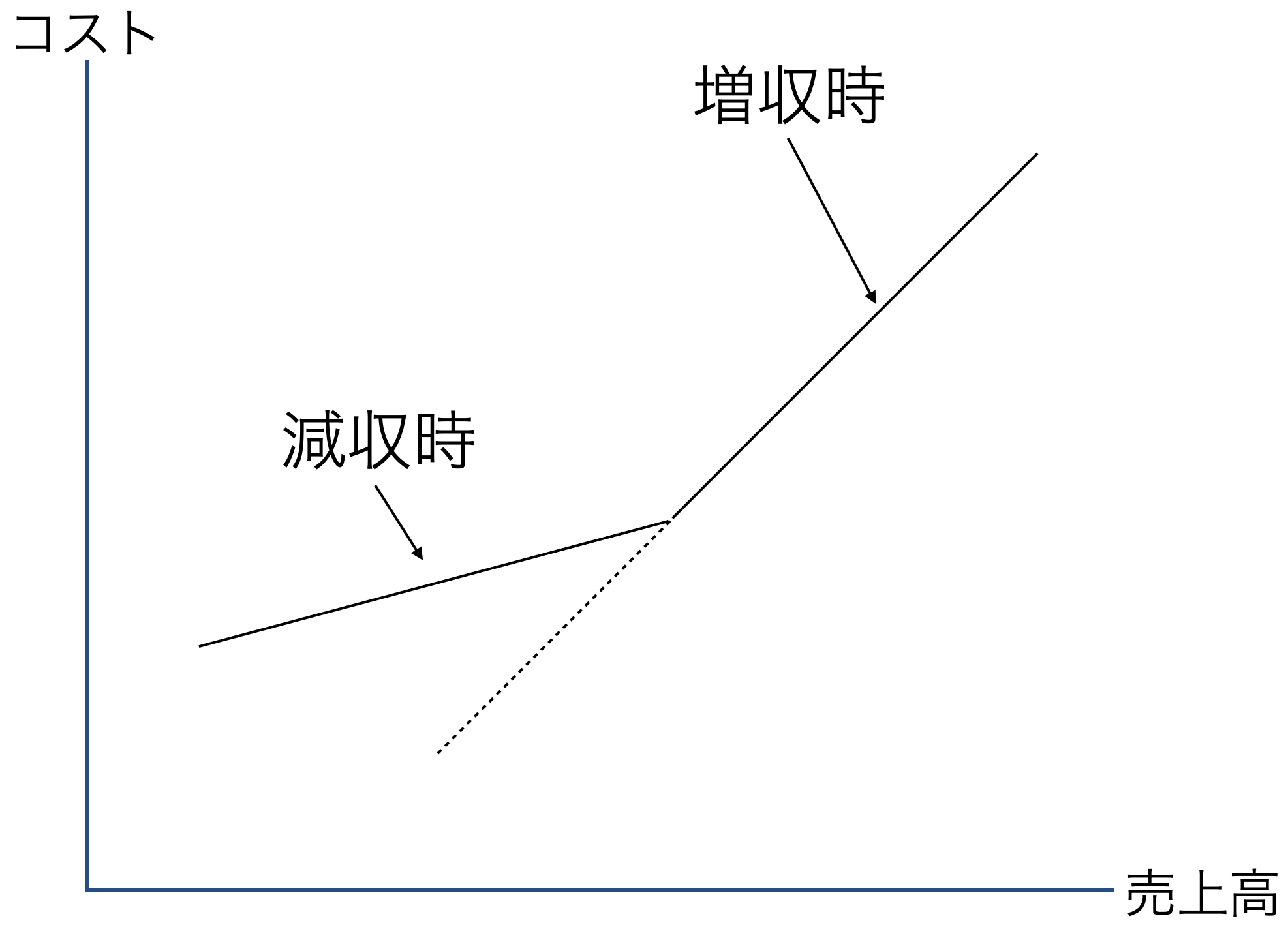
2 非対称なコスト変動
2.1 コストの下方硬直性
伝統的には，コストと活動量(売上高)は比例関係にあるとされてきた
- 売上高が1%上がったら（下がったら）コストも1％上がる（下がる）
だけど， Anderson, Banker, and Janakiraman (2003) は売上高の増加時におけるコストの増加率が，同額の売上高の減少時におけるコストの減少率より小さい場合があることを発見。
売上高の変化とコストの変化は単純な比例関係を想定していたけど，どうも違うみたいだ。
- 増収時のコスト増加率よりも，減収時のコスト減少率が低い。これをsticky cost と呼ぼう(日本では下方硬直性と呼ぶ)(Anderson et al. 2003)
- 後にstickyとは逆パターンが起こることも発見される。これはanti-sticky (Kama and Weiss 2013)
- 近年では両方の現象に同じ原因を想定して，asymmetric cost behavior (コストの非対称性)と呼ぶ (Banker and Byzalov 2014)
2.2 その後
なんでこんなことが起こるんだろう？
- コストの中にはそんな簡単に増減させられないものがある。売上高の変化にコストの変化が追いついていない (安酸 and 梶原 2009)
- 経営者は，合理的な意思決定の結果としてコストをstickyにするんじゃないか (安酸 and 梶原 2009)
- 経営者の利己的な行動の結果としてコストがstickyになるんじゃないか (Chen, Lu, and Sougiannis 2012)
それぞれの仮説に従う証拠を集めよう
- 経営者が特定の行動をとるインセンティブを持つときに，コストの動きはどうなる？ (Kama and Weiss 2013)
- 経営資源の需要が異なるときにコストの動きがどうなる？ (Banker, Byzalov, and Plehn-Dujowich 2014)
そもそもこの現象は方法論上のカラクリで生じているように見えるだけでは？
Balakrishnan, Petersen, and Soderstrom (2004)
- 変数の決め方が悪い？
- 固定費と変動費の話を言い換えているだけでは？
コストの非対称性があると何が困るの？
- コストの非対称性の経済的帰結は？ (佐久間福嶋濵村 2017)
- 市場はコストの非対称性を織り込んで企業を評価しているのか？ (Anderson, Banker, Huang, and Janakiraman 2007)
- 保守主義会計との関係は？ (Banker, Basu, Byzalov, and Chen 2016)
3 データ分析
公表財務データは基本的にすごく高いデータベースから入手します。
- 典型的には日経NEEDS FinancialQUESTっていうデータベースを使います。
政府の提供するEDINETからもデータをとってくることができますが
提供期間が限られる
XBRLというデータ格納形式の操作性
等の問題から使い勝手が悪く研究目的で使われているのをみたことがありません。
今回は，小笠原先生（甲南大学）と早田さん（神戸大学の大学院生のはず）が抽出し，教育目的で提供してくださっているEDINET経由で取得したデータを使います (小笠原 and 早田 2021) 。
| 変数名 | 内容 | 変数名 | 内容 |
|---|---|---|---|
| f1 | EDINETコード | x20 | 資本金 |
| f2 | 証券コード | x21 | 資本剰余金 |
| f3 | 会計期間終了日 | x22 | 利益剰余金 |
| f4 | 提出日 | x23 | 自己株式 |
| f5 | 当事業年度開始日 | x24 | 評価・換算差額等 |
| f6 | 当事業年度終了日 | y1 | 売上高 |
| x1 | 現金及び現金同等物の残高 | y2 | 売上原価 |
| x2 | 資産 | y3 | 売上総利益又は売上総損失 |
| x3 | 流動資産 | y4 | 販売費及び一般管理費 |
| x4 | 固定資産 | y5 | 給料及び手当 |
| x5 | 有形固定資産 | y6 | 減価償却費/販売費及び一般管理費 |
| x6 | 無形固定資産 | y7 | 研究開発費 |
| x7 | 投資その他の資産 | y8 | 営業利益又は営業損失 |
| x8 | 負債 | y9 | 営業外収益 |
| x9 | 流動負債 | y10 | 営業外費用 |
| x10 | 短期借入金 | y11 | 支払利息 |
| x11 | 1年内償還予定の社債 | y12 | 経常利益又は経常損失 |
| x12 | 1年内返済予定の長期借入金 | y13 | 特別利益 |
| x13 | 固定負債 | y14 | 特別損失 |
| x14 | 社債 | y15 | 税引前当期純利益又は税引前当期純損失 |
| x15 | 転換社債型新株予約権付社債 | y16 | 親会社株主に帰属する当期純利益又は親会社株主に帰属する当期純損失 |
| x16 | コマーシャル・ペーパー | y17 | 包括利益 |
| x17 | 長期借入金 | z1 | 営業活動によるキャッシュ・フロー |
| x18 | 純資産 | z2 | 減価償却費/営業活動によるキャッシュ・フロー |
| x19 | 株主資本 | z3 | 投資活動によるキャッシュ・フロー |
| z4 | 財務活動によるキャッシュ・フロー |
Code
ufo <- ufo |>
rename(
id = f1,
code = f2,
end = f3,
submit = f4,
year_start = f5,
year_finish = f6,
cash = x1,
asset = x2,
current_assets = x3,
fixed_assets = x4,
tangible = x5,
intangible = x6,
other_assets = x7,
liability = x8,
current_liability = x9,
short_debt = x10,
bonds_due_within_1_year = x11,
long_term_debt_due_within_1_year = x12,
fixed_liability = x13,
bonds = x14,
convertible_bonds = x15,
commercial_paper = x16,
long_debt = x17,
net_worth = x18,
shareholders_equity = x19,
capital_stock = x20,
capital_surplus = x21,
retained_earnings = x22,
treasury_stock = x23,
valuation_and_translation_adjustments = x24,
sales = y1,
cogs = y2,
gross = y3,
sga = y4,
salary = y5,
depreciation = y6,
r_and_d = y7,
operating_income_loss = y8,
non_operating_income = y9,
non_operating_expenses = y10,
interest = y11,
ordinary_income = y12,
extraordinary_income = y13,
extraordinary_losses = y14,
income_before_income_taxes = y15,
net_income_attributable_to_owners_of_the_parent = y16,
comprehensive_income = y17,
cf_from_operating_activities = z1,
depreciation_expenses_cf = z2,
cf_investing = z3,
cf_financing = z4
)
ufo <- ufo |>
mutate(code = code / 10) |>
mutate(code = as.character(code))企業名が欲しかったので，日本証券取引所グループから持ってきた会社コードと企業名一覧データをくっつける
3.1 統計モデル
\(Cost\)を何らかの費用（ Anderson et al. (2003) やそれに続く研究では販売費及び一般管理費 ），\(Sales\) を売上高とすると
\[ \log \frac{Cost_{i,t}}{Cost_{i,t-1}} = \beta_0 + \beta_1 \log \frac{Sales_{i,t}}{Sales_{i,t-1}} + \beta_2 Dec_{i,t} \log \frac{Sales_{i,t}}{Sales_{i,t-1}} + \varepsilon_{i,t} \tag{1}\]
ただし，\(i\)は企業，\(t\)は年度を表し，\(Dec\) は企業の売上高が減少した場合に 1，そうでない場合に0を取るダミー変数。
つまり
\[ \begin{cases} \log \frac{Cost_{i,t}}{Cost_{i,t-1}} = \beta_0 + \beta_1 \log \frac{Sales_{i,t}}{Sales_{i,t-1}} + \varepsilon_{i,t} & 増収時 \\ \log \frac{Cost_{i,t}}{Cost_{i,t-1}} = \beta_0 + (\beta_1 + \beta_2 ) \log \frac{Sales_{i,t}}{Sales_{i,t-1}} + \varepsilon_{i,t} & 減収時 \end{cases} \]
となる。ここで，\(\frac{Cost_{i,t}}{Cost_{i,t-1}}(\frac{Sales_{i,t}}{Sales_{i,t-1}})\)はコスト（売上高）の前年比，それにlogをとっているので，前年比コスト（売上高）の変化率，と解釈できる。
増収時と減収時の売上高の変化率に対するコストの変化率が違うかどうかを知りたいので，注目するのは，\(\beta_1\)（増収時）と\(\beta_1 + \beta_2\)（減収時）の差。
- 特に\(\beta_1 > \beta_1 + \beta_2\)，つまり\(0> \beta_2\)のときにコストの下方硬直性があるということになる。
3.2 変数の作成
3.3 記述統計量
3.4 分析
Code
model <- lm(
dlogsga ~ dlogsales + dec_dlogsales,
data = data
)
m <- summary(model)
modelsummary(
list(model),
stars = stars,
estimate = "{estimate}{stars}",
align = 'ld',
fmt = fmt_decimal(digits = 2, pdigits = 3),
gof_map = c("nobs", "r.squared", 'adj.r.squared')
) |>
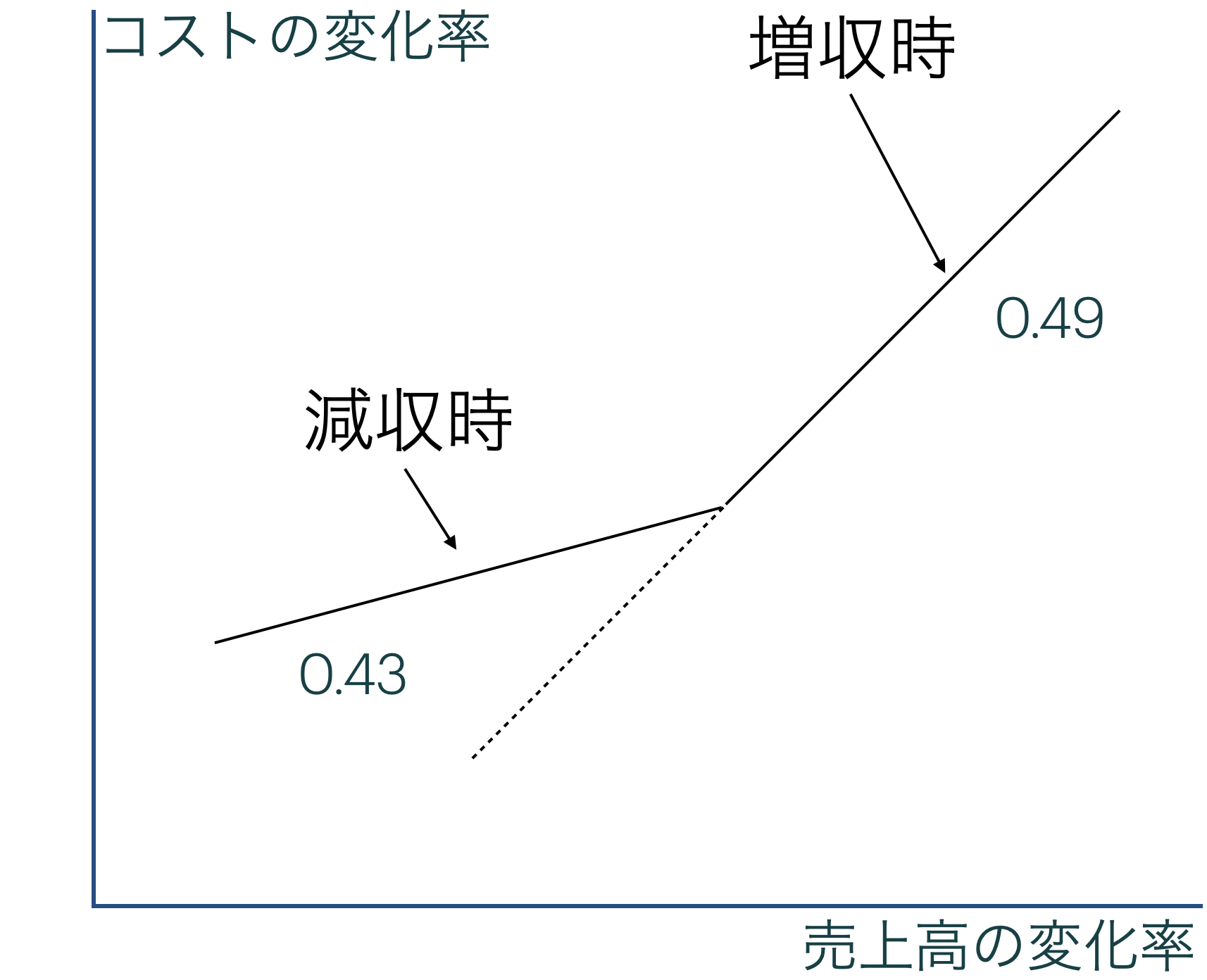
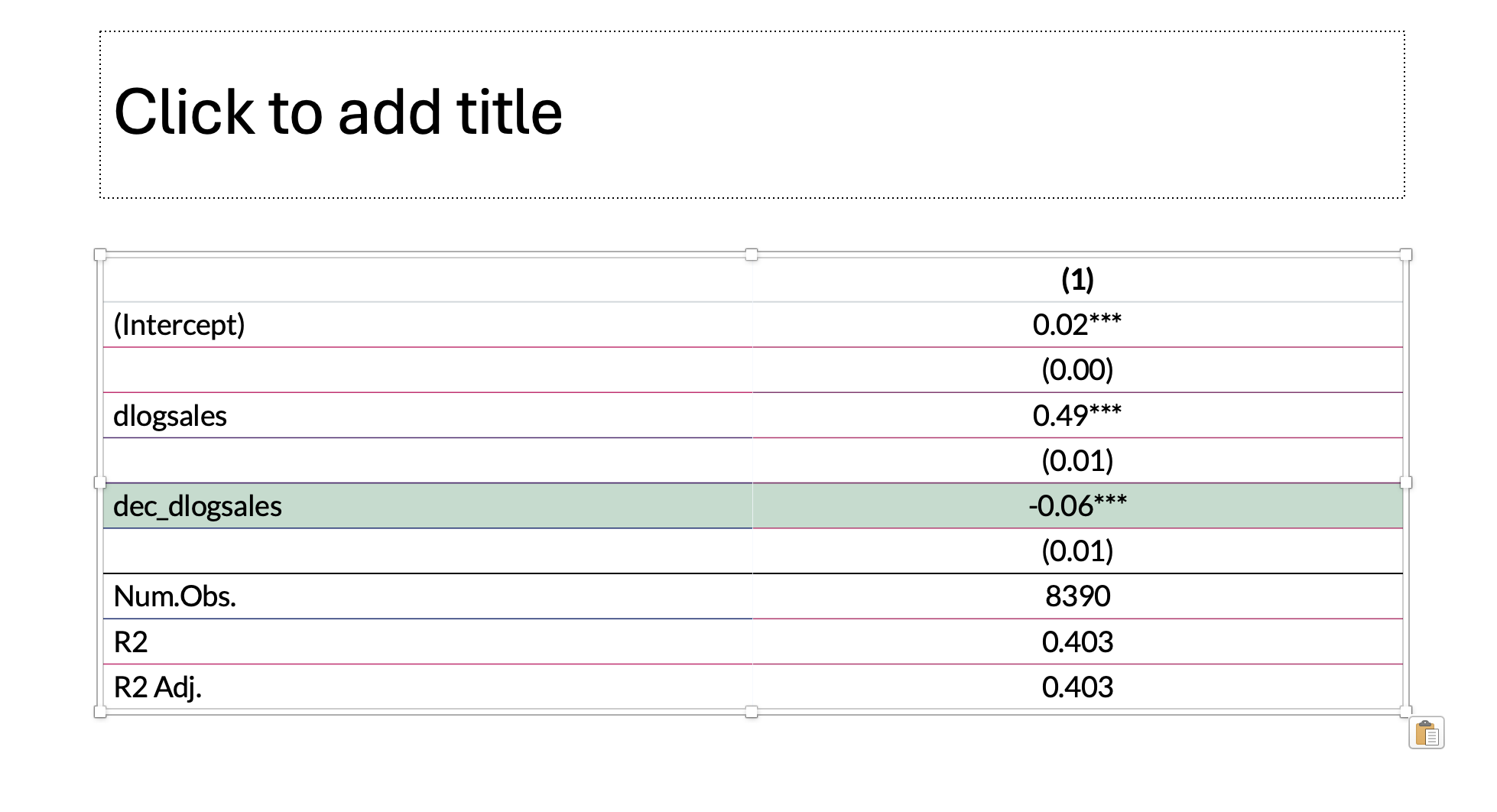
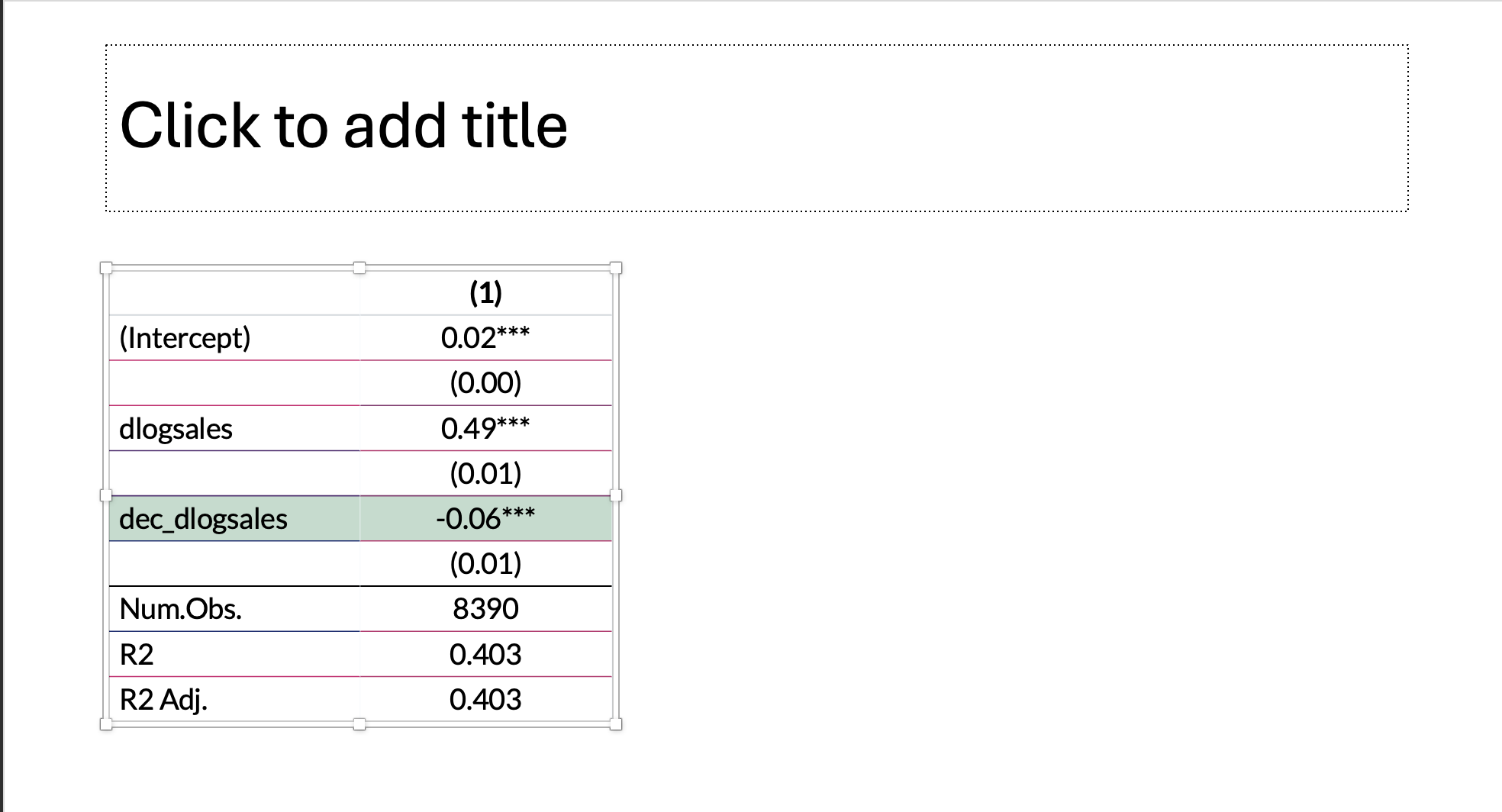
style_tt(i = 5, background = '#C6DBCE')| (1) | |
|---|---|
| (Intercept) | 0.02*** |
| (0.00) | |
| dlogsales | 0.49*** |
| (0.01) | |
| dec_dlogsales | -0.06*** |
| (0.01) | |
| Num.Obs. | 8390 |
| R2 | 0.403 |
| R2 Adj. | 0.403 |
- \(\beta_2\)の係数は有意に負（ -0.06 , p = 0 ）
- コストの下方硬直性が確認された。
3.5 その後の進展: 資源調整コストという考え方
その後の研究で，Bankerらは，このようなコストの非対称性が起こる理由を資源調整コストに求めるように(Banker and Byzalov 2014; Banker, Byzalov, Fang, and Liang 2018)
- 経営においてかかる費用は，経営資源に対する投資を含む
- 特に無形の経営資源（Intangibles）への投資
- 合理的な価値推定が難しく，資産として貸借対照表上に現れない (桜井 2015)
- 例えばブランド価値，研究開発力，営業力，組織文化…
- 合理的な価値推定が難しく，資産として貸借対照表上に現れない (桜井 2015)
- これらは費用，特に販管費に含まれがち
- 特に無形の経営資源（Intangibles）への投資
- 毎年の費用はこれらの経営資源の獲得・維持費だと考える
ある年の売上高が前年より下がったとしても，それに対応して，経営資源を削減できる？
- 前年よりも売上高が下がったから， 従業員(ヒト)の給料をそのぶん下げたり，クビにしたりする？
- 設備を処分する？
- 情報システムを安いのに切り替える？
シナリオA
今期の売上高が利用可能な資源レベルより大きいとき：需要に対応するために資源を所要量獲得
シナリオB
今期の売上高が利用可能な資源レベルより小さいとき：限界資源(marginal resource)を維持することとそれを削除することが無差別になるまで，資源を削減。 資源スラックの維持にかかるコストと資源の廃棄にかかるコストを判断。
シナリオC
利用可能な資源レベルが今期の売上高に対応するのに十分なとき：資源スラックは許容可能な範囲にあるので，元々の資源レベルを維持。
この考えに従うと，固定費と直接費も，資源調整コストの大きさによって区分し直すことができる。
4 Quarto
ところで，
- この資料は全てRstudio内で作成しています。
- 何なら，最近は論文自体も全部Rstudio内で作成しています。
文書なら
- html形式（.
html） - ワード形式（.
docx） - \(\LaTeX\) 形式（.
tex） - pdf形式（.
pdf）
スライドなら
- html形式（.
html） - パワーポイント（.
pptx） - beamer（.
pdf）
その他にも
- webサイト
- 電子書籍（ebook）
などなど色々な形で出力できます
また，
- R
- Python
- Julia
といった様々なプログラミング言語での分析結果を含めることができます
Note
詳しくはQuarto公式ページ
これらは，Rstudioと同じPosit社が提供するQuartoというサービスで実現されます。
ここからは，
- 慣れたらワードやパワポよりも便利
- 分析→修正を繰り返すとき超時短になる
- 再現性のある分析に寄与する
って話をした後で
- Markdown形式で書く
- Quartoでレポート作成
について簡単に説明します
4.1 慣れたらワードやパワポよりも便利
ワード文書は，文書の形式（フォントの種類とか大きさとか枠とか）を調整することと中身書くことを同時にやることになります。
パワポではさらに複雑で，文書や文字，図表の配置と中身を考えることを同時にやります
これってすごく非効率では？
- それぞれの作業に人間の限られた注意力を分散させてしまっている？
Quartoを使うと，中身はテキスト形式で書いていけます。
- スライドなら基本箇条書きです。
- 箇条書きで中身を考える
- 文書とかスライドにして，形式を整える
というふうに作業を分割できます。
使い回しもしやすいです
- テキスト形式で記録されているので，コピーしやすい
文献の引用→文献リスト作成も自動でできるように設定可能
- Zoteroというサービスと統合させると，文献リストを簡単に挿入できます。
数式の挿入はワードよりはるかに便利
- $ で囲むだけ \(y = ax +b\)
スライドのレイアウトはほぼ自動
- 最低限の設定で自動レイアウトしてくれるので，文字の大きさや配置等，いちいち調整しなくてもいい
- 一括設定なので，全体的に調和の取れた形で作れる
4.2 分析→修正を繰り返すとき超時短になる
普通？分析の結果はスライドや文書ファイルにまとめる。その際分析結果の図表をRなどの分析環境からコピーして貼る
通常分析はやってみて検討してやり直してを繰り返す
- 面倒臭いし間違いも増える
Quartoなら
- 分析コードを変えるだけ。結果だけ変わった図表が出力される
4.3 再現性のある分析に寄与する
データ分析において重要なことの一つが「再現性」
- 他の人がやっても同じ結果が再現できるようにする
- データ分析の処理方法を第三者が検証可能な形にしておく
Quartoを使って分析からレポート作成までしておくとコードとその出力結果を一つのドキュメントにまとめることができます。
- どんなデータを読み込んで
- どんな統計処理をして結果を出して
- どんなふうに結果を解釈してレポート・スライドを作ったのか
といったことが明確に記録される
これにより、どのようなコードが実行され、どのような結果が得られたかを一目で確認でき、他の人が同じコードを実行することで同じ結果を再現できます。
5 Quartoでレポート作成
Quartoでレポートやスライドを作るにあたって，分析コード（RとかPythonとか）以外に必要なのが，Markdown記法に関する知識
- ただし，Rstudioを使うのであれば，ほとんどの操作はワードとかと同じようにショートカットでもできる
特にスライドやWebページを作るとき，デザインに凝りたいならhtmlやcssの知識が必要です
- 特にこだわらないならなしでも大丈夫です。
5.1 Markdownの主な操作
見出し
「#」の後に半角スペースで見出しになります。「##」のように増やすと小見出しになります。
箇条書き
「-」の後に半角スペースで箇条書きになります。
「1.」の後に半角スペースで番号付きリストになります。
太字と斜め字
「*」で囲むとその間の文字が 「斜めに」（⌘ + Iでも）
「**」で囲むとその間の文字が 太字になります。（⌘ + Bでも）
コード
「`」で囲むとその間の文字がコードになります（⌘ + Dでも）
「```」と打つとコードブロックが作れます
1+1
lm(y~x,data=data)数式
「$」で囲むと数式になります : \(y = ax +b\)
「$$」で囲むと真ん中寄せの数式に
\[ y = ax +b \]
横線
「-」を3つ連続で打つと横線が出ます
5.2 Quartoでレポート作成
ファイルの作成
内容の編集
ページ分けはレベル2以上の見出し（##）か，水平線
その他色々できます（公式サイト）
完成したら，⇨Renderボタンを押す
5.3 YAMLヘッダー
文書の一番上，囲まれている部分はyamlヘッダーとかいって，タイトル，著者情報，日付なんかを入れられる。
スライドの細かい設定もここをいじったらできる（めちゃくちゃ色々設定できる）
revealjsというのはスライドの形式。ここをhtmlとかpdfとかdocxとかに変えたら，違う形式で出力できる
5.4 まとめ
Quartoを使うと，データ分析からレポート・スライド作成まで一気通貫にできます
- これは，データの操作から結果までを記録に残しつつ一元管理するという意味で再現性の意味でも望ましいです
慣れたらwordやpower pointよりも便利です
- 流石にイラストは描けないけど
分析・執筆作業と体裁を整える作業を分離できるので作業効率が上がる（気がします）
期末レポート作る際とかに試してみてください
6 実習
コストの下方硬直性の研究は，販売費及び一般管理費（SG&A）を対象として研究されてきました。
一方で，販管費には何百，何千もの費目が含まれているとも言われます(Tracy and Tracy 2014)
- つまり，複数の費目に関する意思決定が混ざった結果
経営者の戦略的な意思決定を捉えるためには，より細分化された費目を用いた分析も役に立ちそうです 。
6.1 課題
以下の分析コードと説明内容をQuartoのqmdファイルで提出してください。分析コードは実行可能なようにR Code Chunkに書いてください。
- 給料及び手当について，コストの下方硬直性が存在するか推定してください。また，結果から経営者のどのような意思決定が想像できるか説明してください。
- 研究開発費について，コストの下方硬直性が存在するか推定してください。また，結果から経営者のどのような意思決定が想像できるか説明してください。
6.2 解答例
Code
data <- data |>
group_by(code) |>
mutate(lag_salary = lag(salary),
lag_r_and_d = lag(r_and_d),
lag_cogs = lag(cogs),
dlogsalary = log(salary/lag_salary),
dlogr_and_d = log(r_and_d/lag_r_and_d),
dlogcogs = log(cogs/lag_cogs))
data <- data |>
mutate(dlogr_and_d = ifelse(is.infinite(dlogr_and_d) | is.nan(dlogr_and_d), NA, dlogr_and_d))
# 回帰
Salary <- lm(dlogsalary ~ dlogsales + dec_dlogsales, data = data)
RandD <- lm(dlogr_and_d ~ dlogsales + dec_dlogsales, data = data)
cogs <- lm(dlogcogs ~ dlogsales + dec_dlogsales, data = data)
list(Salary = Salary,RandD = RandD,CoGS = cogs) |>
modelsummary(stars = stars,
estimate = "{estimate}{stars}",
align = 'lddd',
fmt = fmt_decimal(digits = 2, pdigits = 3),
gof_map = c("nobs", "r.squared", 'adj.r.squared')) |>
style_tt(i = 5, background = '#C6DBCE') | Salary | RandD | CoGS | |
|---|---|---|---|
| (Intercept) | 0.03*** | 0.02** | 0.01*** |
| (0.00) | (0.01) | (0.00) | |
| dlogsales | 0.32*** | 0.02 | 0.90*** |
| (0.02) | (0.07) | (0.01) | |
| dec_dlogsales | -0.05** | 0.11 | 0.09*** |
| (0.03) | (0.10) | (0.01) | |
| Num.Obs. | 3406 | 3395 | 8322 |
| R2 | 0.169 | 0.001 | 0.767 |
| R2 Adj. | 0.169 | 0.000 | 0.767 |
- 人件費は下方硬直的
- 減収時直ちに減俸や解雇を通した人件費の抑制行動をとるわけではない。
- 人的資源を保持した方が，解雇⇨再獲得・再教育よりもコストが低いと判断している可能性？
- 研究開発費は有意でない。そもそも売上高の変動とも関係ない。
- 業績に関わらず一定の金額を支出するような企業が多い可能性？
- 売上原価は，反下方硬直的
- 売上高が下がった時，売上高の増加時よりも急な傾きで減少する。
販売費及び一般管理費の明細を使っていろんな費目を推定してみた論文
参考文献
2025 経営データ分析（会計）