11 コスト構造とCVP関係の分析

佐久間智広

2024/06/21

1 はじめに

データを使った管理会計の分析，として最初に思い浮かぶ

• コスト構造の分析
• CVP分析

を扱います。

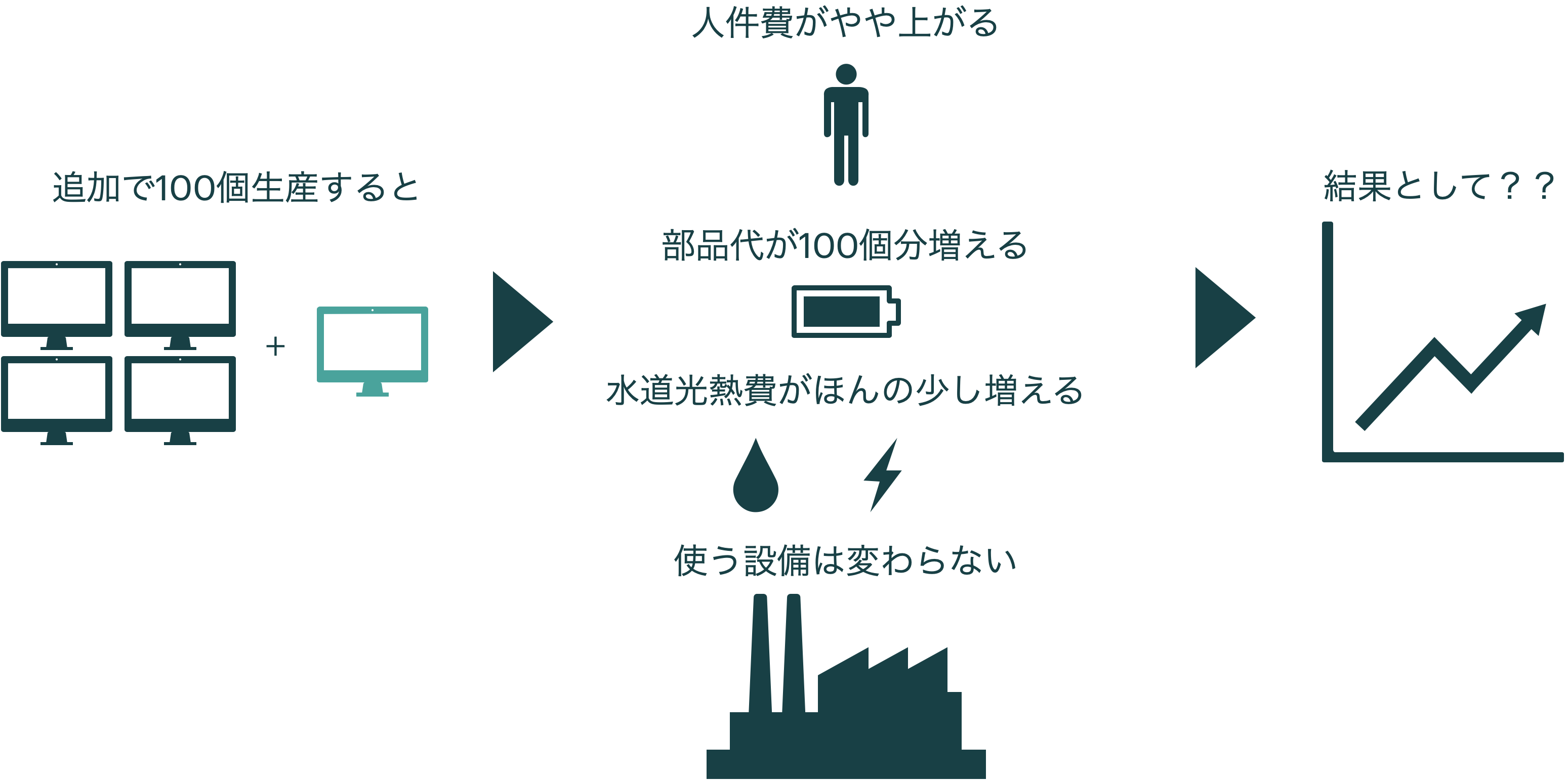
企業は，自社コストの発生容態を把握したいと考えています。というのも企業は…

• 経営戦略の策定・実施
• 長期的な投資や計画の策定
• 年次計画の策定・検証，特に
  • 利益計画→製造計画の策定・検証

などを行うにあたって，コストがどのように発生しているかを知りたいと思うからです。

コストの発生容態が把握できると，製品の単価等のデータを使って，販売量と利益との関係を計算できます

• 何個以上売れればコストを回収できるか
• 利益目標を達成するためには，何個以上売る必要があるか
  • それを踏まえてどれぐらいの生産を計画すれば良いか
  • 生産計画に合わせて，
    • どれぐらいの人員を確保すれば良いか
    • どれぐらいの材料を購入すれば良いか
    • …

2 コスト構造の推定

2.1 コストビヘイビアの分析

営業量とコストとの関係は，必ずしも一様ではない。

• 生産量の増加に伴って直接労務時間や機械稼働時間は増えそう
• 機械設備の減価償却費や工場事務員の基本給は活動量にかかわらず一定

コストビヘイビア (cost behavior)

営業量（生産量・販売量・操業度）の変化に対する原価の変化の仕方

コストビヘイビアの情報は，経営のこんな場面で役立つ

• 損益分岐点分析もしくはCVP分析
• 自製か外注か，注文を受けるか否か，といった短期的な意思決定
• 貢献利益ベースの業績評価
• 変動予算

2.2 コストビヘイビアの視点から見たコスト

• 変動費 Variable Costs
• 固定費 Fixed Costs
• 準固定費 Semivariable (or mixed) Costs

注意点として，この分類は，正常な範囲 （正常操業圏） Relevant rangeでのみ有効であるということ

• 突然活動が何十倍になる，とか突然0になる，とかいうことは想定していない

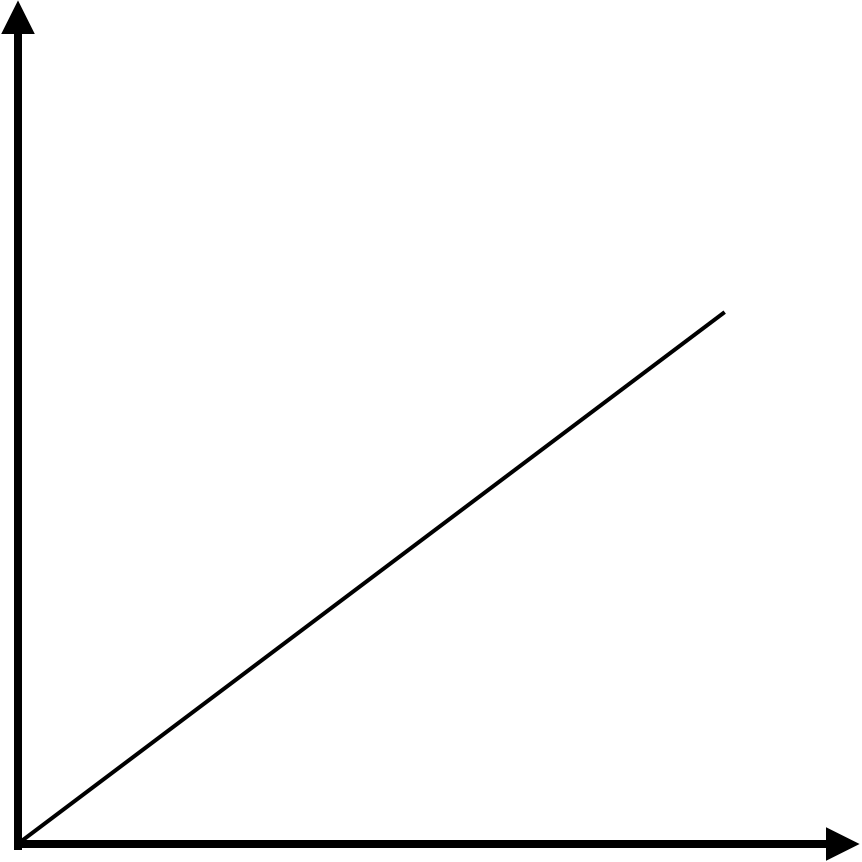
2.2.1 変動費 Variable Cost

全体として生産量もしくは活動量に応じて変化するようなコスト

• 販売手数料
• ガソリン代
• その他

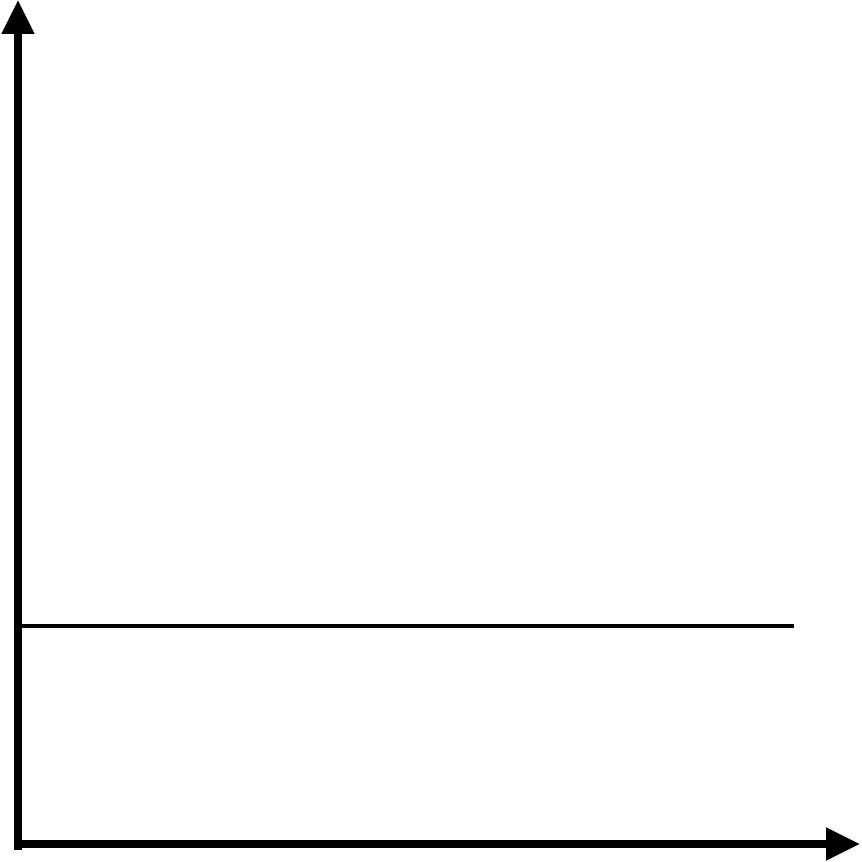
2.2.2 固定費 FIxed Cost

製造量や活動量によらず一定に発生するコスト

• 家賃
• 固定資産税
• 保険料
• ライセンス料
• その他

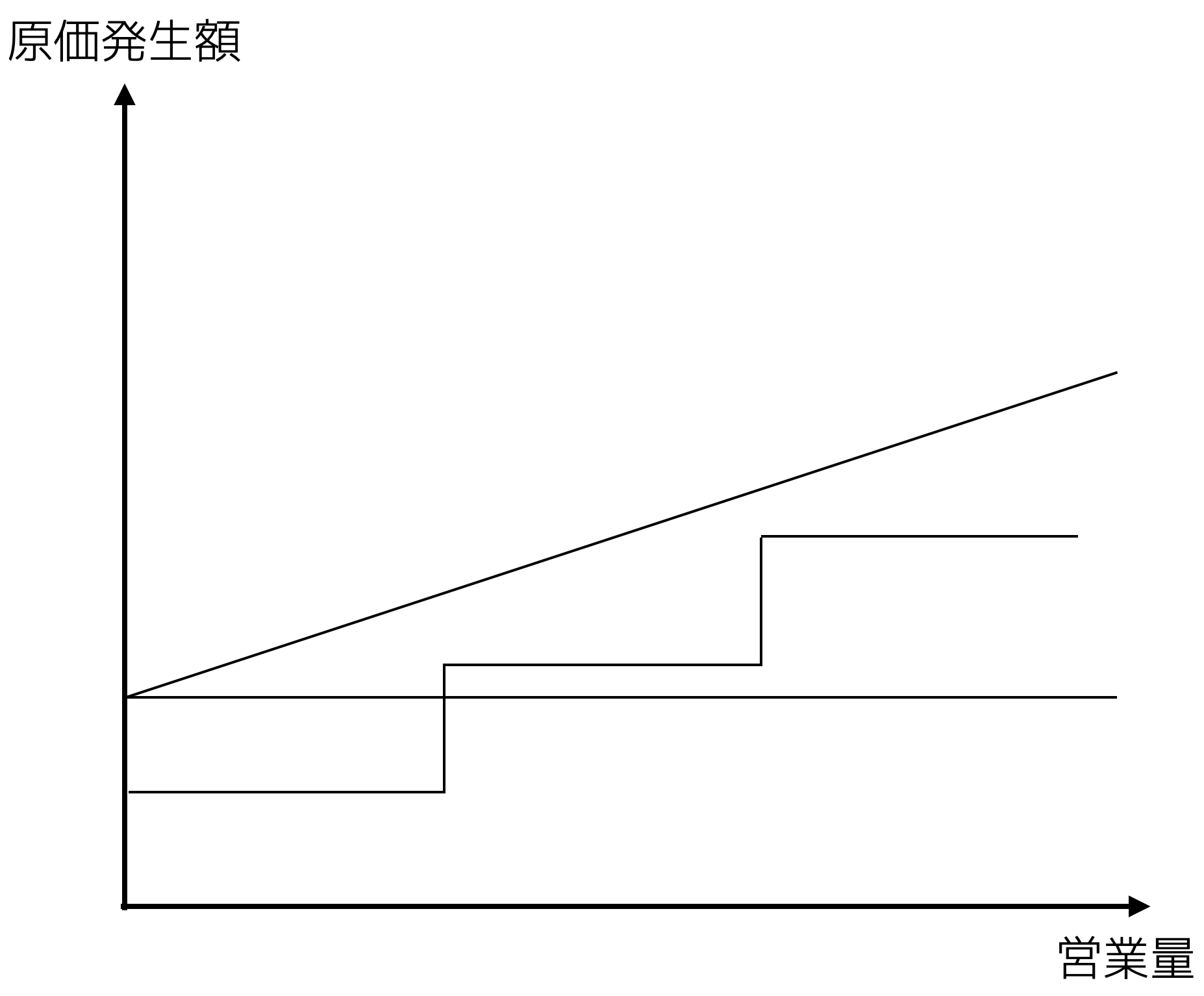
2.2.3 準変動費 Semivariable Costs

固定的要素と，変動的要素が混じっている

• 監督者の給料

製造原価は全体として準変動費

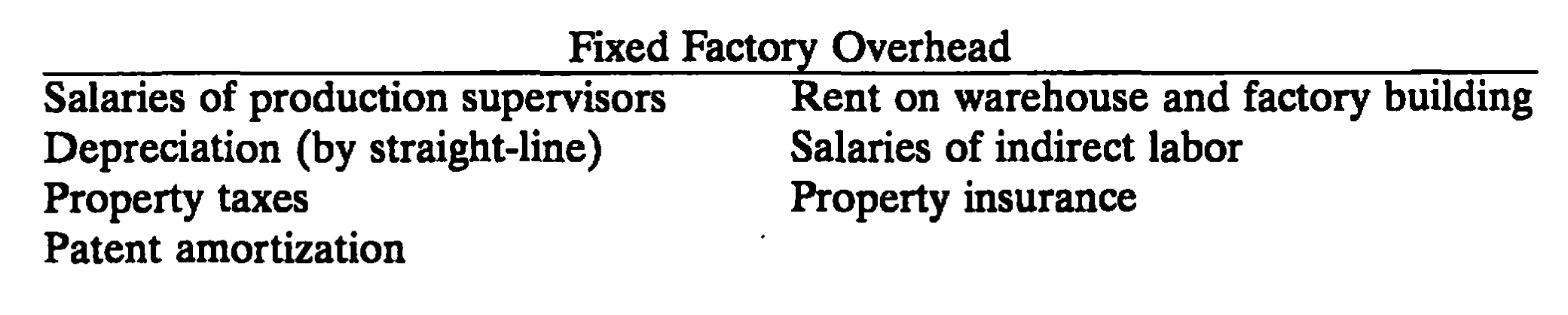
2.3 固定費のタイプ: Committed と Discretionary

固定費，といっても実際に本当に固定されているものはない

• 長期的に見ると全て変動費とも言える

ただ，1年単位とか，短期的に見ると固定費は確かに存在する。その中には，Discretionary (もしくはmanaged, programmed)と，Committedがある。

Discretionary

---

経営者の意思決定や製造量の変化によって変化する固定費。ポリシーコストとも

• 広告費，研修・訓練費用，研究開発費など

Committed

---

過去の意思決定（コミット）の結果生じている固定費

• 家賃，減価償却費，保険，役員報酬など

経営者のこれからの意思決定によって変化させることができる度合いによる分類，とも考えられる

3 固変分解

コストの分析をするためには，準変動費を固定部分と変動部分に分解することが必要

でも固定費と変動費を分けるのはそこまで簡単ではない。

• 企業で最も多く利用されてきたのは勘定科目法（勘定科目ごとに，分析の実施者が判断する）でも，
  • 勘定科目ごとに固定費と変動費が決まっているのか，
  • 準変動費はどうするのか？
  • そもそも，何百・何千にも分けられる企業の費目を勘定科目ごとに分類できるのか？(Tracy and Tracy 2014)
• といった問題も (福嶋, 新井, and 松尾 2014)

理論的に最も優れているのは，データからの推定，特に回帰分析を使った統計的な方法 (福嶋 et al. 2014; 谷 2022)

• 固定費・変動費が混じった勘定科目も問題なく含めて推定できる

3.1 準変動費（混合費）の分析

\[ y=a+bx \]

ここで

\(y\): 分解したい準変動費

\(x\): 活動量の代理変数；生産量，売上高，直接労務時間など

\(a\): 固定部分

\(b\): 変動部分（\(x\) 1単位あたりの変動率）

固変分解の方法はいくつかある

高低点法 (the high-low method)

過去の原価データから代表的なデータを2つ選び，その2点を通る直線を計算する。

スキャッターグラフ法 (the scattergraph method)

縦軸に原価，横軸に営業量を取り，過去の原価データをプロットする。その後，目分量で傾向線を当てはめる

最小二乗法 (the least square method)

従属変数を原価，独立変数を営業量として，単回帰分析を行い，費用線を推定する。

以下で順番に見ていきます

3.1.1 データ

options(scipen = 999)
options(digits = 3) 
if (!require("pacman")) install.packages("pacman") 
pacman::p_load(tidyverse, magrittr, here,
               estimatr, modelsummary,
               broom, tinytable) 

month <- c(1:12)
amount <- c(9, 19, 11, 14, 23, 12, 12, 22, 7, 13, 15, 17)
money <- c(15, 20, 14, 16, 25, 20, 20, 23, 14, 22, 18, 18)

data <- tibble(month, amount, money)
tt(data) |> style_tt(align = "r")

month	amount	money
1	9	15
2	19	20
3	11	14
4	14	16
5	23	25
6	12	20
7	12	20
8	22	23
9	7	14
10	13	22
11	15	18
12	17	18

data |>  
  ggplot(aes(x = money, y = amount)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal()

3.2 高低点法 (the high-low method)

過去の原価データから代表的なデータを2つ選び，その2点を通る直線を計算する。

• 高低点法なので，データの中で高い点と低い点を選ぶなどする

連立方程式を立てて計算すれば良い

• 前の例だと，\((x,y)=(7,14), (23,25)\)の2点を使う

\[ \left\{ \, \begin{aligned} & 25 = a + 23b \\ & 14 = a + 7b \end{aligned}\right. \]

\[ \begin{aligned}11&=16b \\b&=0.6875 \\a&=9.1875 \\ y&= 9.1875 + 0.6875x\end{aligned} \]

tt(data) |> style_tt(align = "r")

month	amount	money
1	9	15
2	19	20
3	11	14
4	14	16
5	23	25
6	12	20
7	12	20
8	22	23
9	7	14
10	13	22
11	15	18
12	17	18

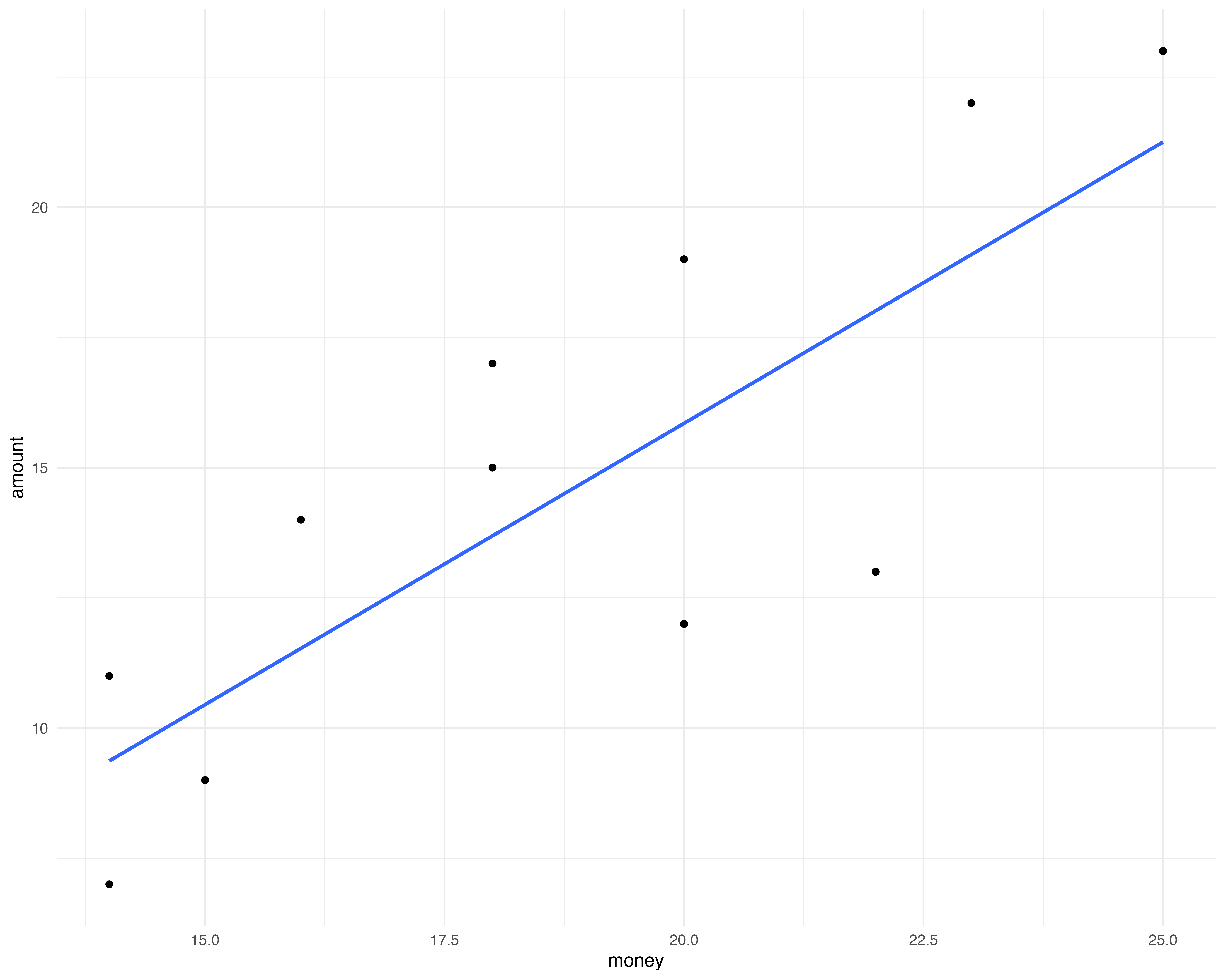
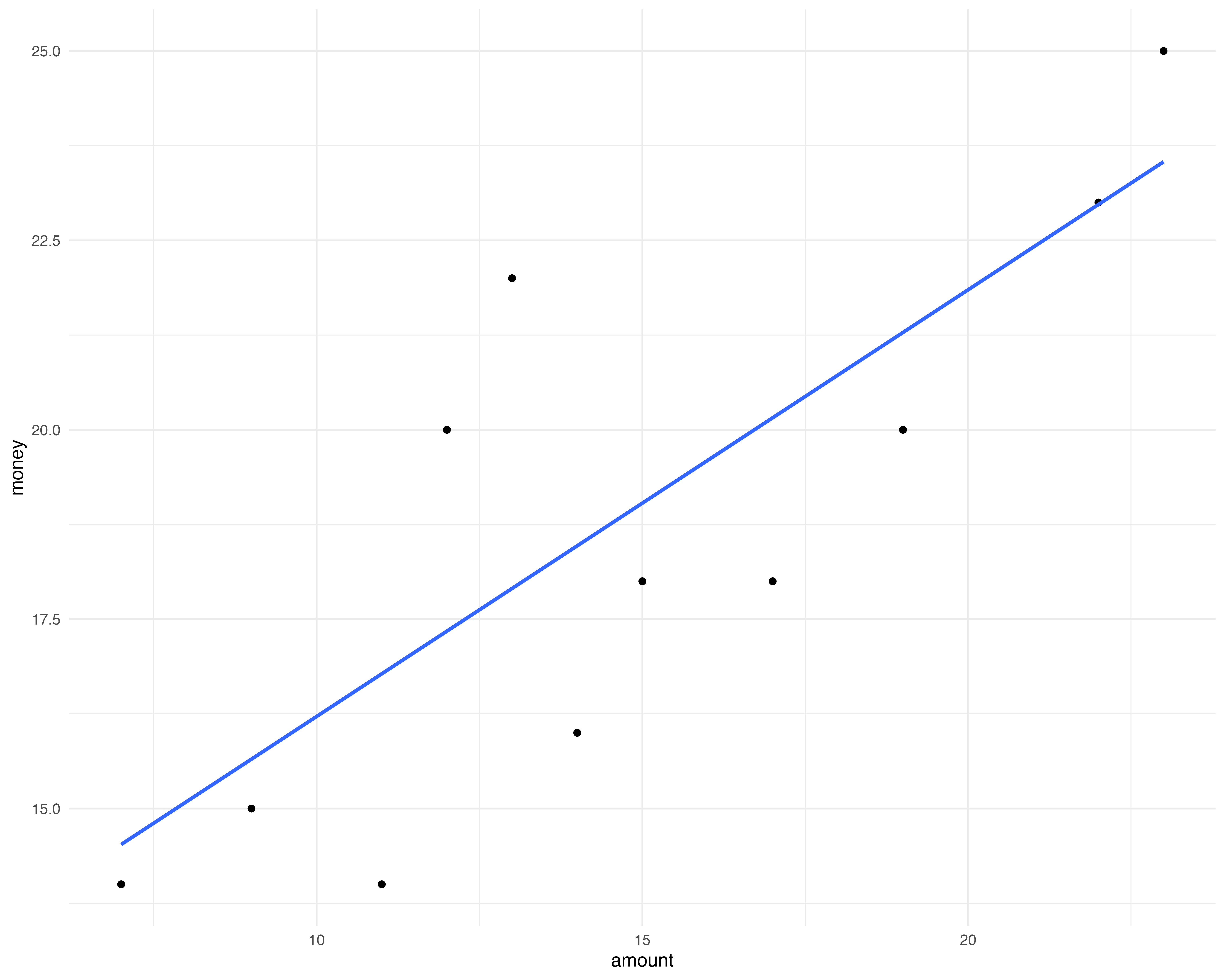
3.3 スキャッターグラフ法 (the scattergraph method)

縦軸に原価，横軸に営業量を取り，過去の原価データをプロットする。その後，目分量で傾向線を当てはめる

• 線を引いてみたら，切片は$6だった。これを手がかりに
• 23時間(h)の時のコストは$25
• 固定費は切片の$6だから，変動費部分は25-6=19
• 変動費率は\(\$19/23h=0.8261\$/h\)
• よって \(y = 6 + 0.8261x\)

data %>% 
  ggplot(aes(x = amount, 
             y = money)) +
  geom_point() +
  geom_abline(slope = 0.8261, 
              intercept = 6) +
  theme_minimal()

3.4 最小二乗法 (The Method of Least Squares; Regression Analysis)

直線と各データの誤差を最小にする線が最も良い線であろう

誤差を全部足したらしたらゼロになる点を探す。

\[ E(u)=0 \]

data |>  
  ggplot(aes(x = amount, 
             y = money)) +
  geom_point() +
  geom_smooth(method = "lm", 
              se = FALSE) +
  theme_minimal()

金額を \(y\),生産量を \(x\) ，直線と過去のデータの誤差を \(u\) とする。 \(i\)は各観測を表す

\[ y_i = \beta_0 + \beta_1x_i+u_i \]

について，誤差

\[ u_i = y_i - \beta_0 - \beta_1x_i \]

が最小となる \(\beta_0\) と \(\beta_1\) を探す。

ということは，\(|u|=0\) が理想

• 絶対値の最小化問題

→それぞれの残差を2乗したものをすべて足しあわせて，それを最小化すれば良い。

data |> tt() |> 
  style_tt(align = "r") 

month	amount	money
1	9	15
2	19	20
3	11	14
4	14	16
5	23	25
6	12	20
7	12	20
8	22	23
9	7	14
10	13	22
11	15	18
12	17	18

数式で表すと，

\[\sum_{i=1}^n \hat{u}_i^2= \sum_{i=1}^n (y_i -\hat{\beta_0}-\hat{\beta_1}x_i)^2\]

が最も小さくなる\(\hat{\beta_0},\hat{\beta_1}\)を求めれば良い。2次関数の最小値問題。微分して0，とすると計算しやすいので，\(\hat{\beta_0},\hat{\beta_1}\)それそれで微分して

\[ \begin{equation}\left\{ \, \begin{aligned}&\frac{\partial \Sigma}{\partial \hat{\beta_0}} = \sum_{i=1}^n (y_i -\hat{\beta_0}-\hat{\beta_1}x_i) = 0 \\&\frac{\partial \Sigma}{\partial \hat{\beta_1}} = \sum_{i=1}^n x_i(y_i -\hat{\beta_0}-\hat{\beta_1}x_i) = 0 \end{aligned}\right.\end{equation} \]

という連立方程式を解けば良い。

\[ \begin{equation} \left\{ \, \begin{aligned} &\sum_{i=1}^n (y_i -\hat{\beta_0}-\hat{\beta_1}x_i) = 0 \\ &\sum_{i=1}^n x_i(y_i -\hat{\beta_0}-\hat{\beta_1}x_i) = 0 \end{aligned}\right. \end{equation} \]

上の式から

\[ \begin{split}&\Sigma y_i - n \hat{\beta_0} - \hat{\beta_1}\Sigma x_i = 0 \\\hat{\beta_0} &= \frac{1}{n} (\Sigma y_i - \hat{\beta_1}\Sigma x_i) \\&= \bar{y} - \hat{\beta_1} \bar{x}\end{split} \]

下に代入して

\[ \begin{split}\Sigma x_i \{y_i - (\bar{y} - \hat{\beta_1}\bar{x}) - \hat{\beta_1}x_i\} &= 0 \\ \Sigma x_i \{(y_i - \bar{y}) - \hat{\beta_1}(x_i - \bar{x})\} &= 0 \\\Sigma x_i (y_i - \bar{y}) - \hat{\beta_1}\Sigma x_i (x_i - \bar{x}) &= 0 \\\end{split} \]

\[ \Sigma (x_i - \bar{x})(y_i - \bar{y}) - \hat{\beta_1}\Sigma (x_i - \bar{x}) (x_i - \bar{x}) = 0 \]

よって

\[ \hat{\beta_1} = \dfrac{\Sigma (x_i - \bar{x})(y_i - \bar{y})}{ \Sigma (x_i - \bar{x})^2} = \dfrac{ x \mbox{と}y\mbox{の共分散}}{ x\mbox{の分散}} \]

\[ \hat{\beta_0} = \bar{y} - \dfrac{\Sigma (x_i - \bar{x})(y_i - \bar{y})}{ \Sigma (x_i - \bar{x})^2} \bar{x} \]

実際にデータを入れて計算すると

\[ y = 0.563x+10.584 \]

reg <- lm(money ~ amount, data = data) 

result <- list(reg)
msummary(dvnames(result),
         stars = TRUE,
         gof_map = c('nobs',
                     'r.squared',
                     'adj.r.squared'), 
         title = '推定結果') 

推定結果

	money
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept)	10.584***
	(2.180)
amount	0.563**
	(0.143)
Num.Obs.	12
R2	0.608
R2 Adj.	0.569

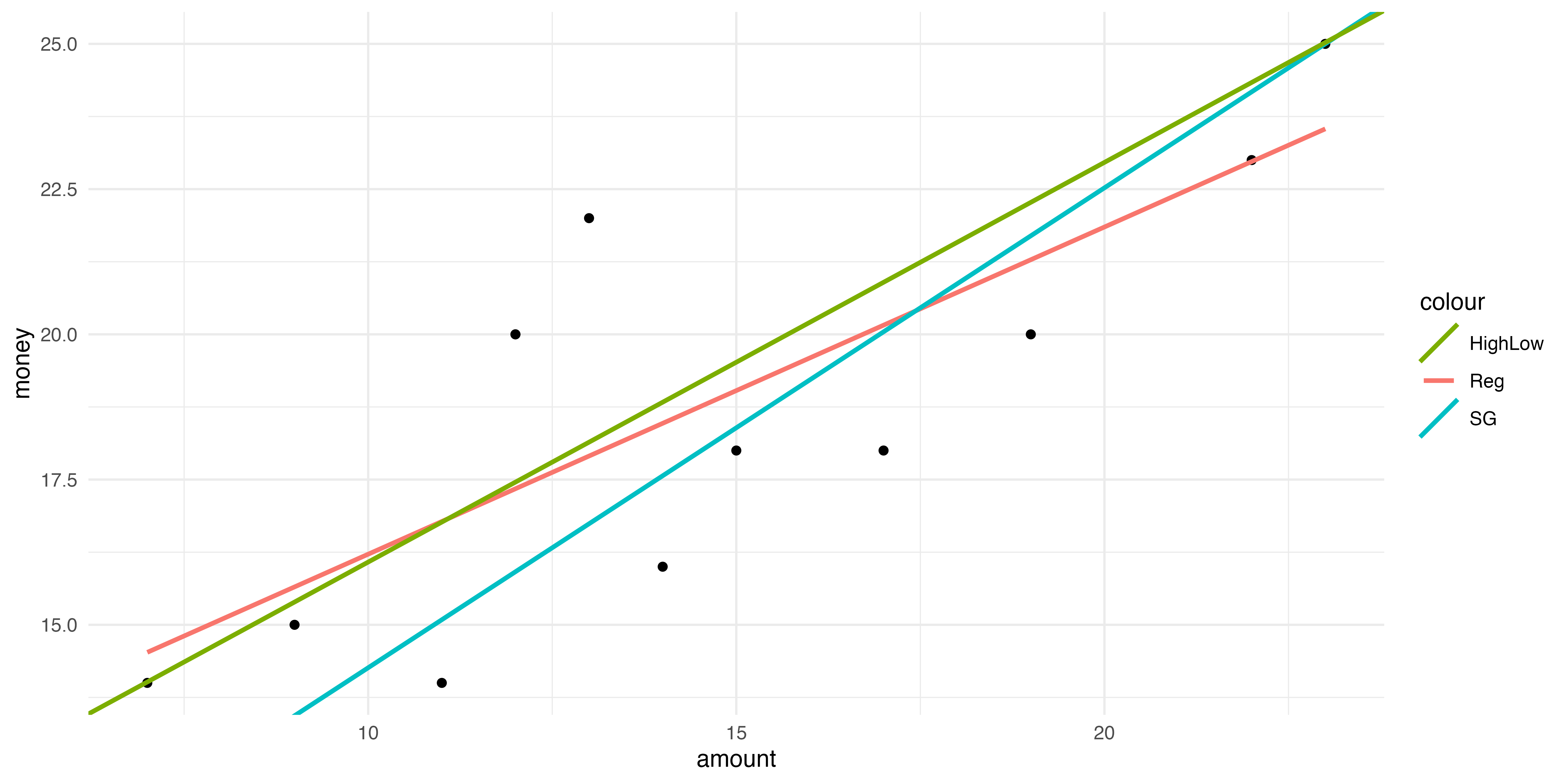
3.4.1 3つの推定方法の比較

方法によって推定値に大きな違いが生じうる。

最も正しそうな方法は？

	高低点法	スキャッターグラフ法	最小二乗法
切片(固定費)	9.188	6	10.584
傾き（変動費率）	0.688	0.826	0.563

data |>  
  ggplot(aes(x = amount, y = money)) +
1  geom_point() +
2  geom_smooth(method = "lm",
              se = FALSE, 
              linewidth = 1, 
              aes(colour="Reg")) +
3  geom_abline(linewidth = 1,
              aes(slope = 0.8261, 
                  intercept = 6, 
                  color = "SG")) +
4  geom_abline(linewidth = 1,
              aes(slope = 0.688, 
                  intercept = 9.2, 
                  color = "HighLow")) +
  scale_color_manual(values = c(Reg = '#f8766D', 
                                SG = '#00BFC4', 
                                HighLow = '#7cae00')) +
  theme_minimal()

1

散布図の作成

2

回帰分析(lm)の結果を描く。seは標準誤差を影で表示するオプション。今回は非表示

3

スキャッターグラフ法での線を描く

4

高低点法での線

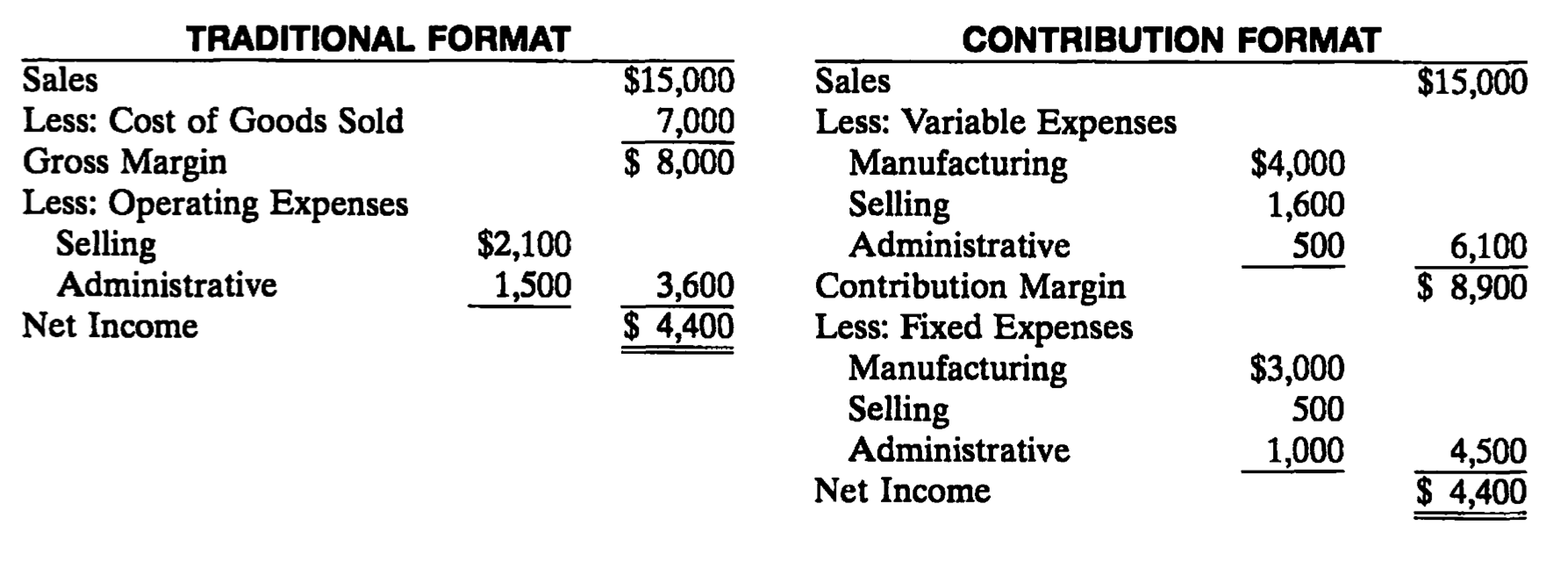
3.5 損益計算書の貢献利益的アプローチ

ちなみに，普通の損益計算書と直接原価計算方式による損益計算書では，このように少し順番が組み変わります。売上原価の一部が，変動費・一部が固定費なので，こんな感じで集計されます。

3.5.1 どんな時に役立つ？

損益分岐点や，利益目標を達成するための販売数を算出できる

• 事業の開始・継続・撤退の判断に役立つ
• 販売予測と組み合わせ，黒字を確保できそうか，利益目標を達成できそうかを判断する
• 工場の製造予定を立てるために役立つ
• どれぐらい作れるような人員や設備を確保するか？

重要な点は，直接原価計算による営業利益と，全部原価計算による営業利益は，必ずしも一致しないということ。

• 期首在庫ゼロ，期末在庫ゼロの時のみ一致

これは，固定費の扱いに起因する。

• 直接原価計算では固定製造費用を期間原価として扱うので，全額がその期に配分される。
• 全部原価計算では，直接原価計算で固定費として扱われる固定製造費用が製造費用に含まれるため，在庫の原価として翌期に持ち越される。

4 CVP関係の分析

4.1 CVP関係 (cost-volume-profit)

• 企業にとって最も基本的な会計の関係
• 利益 = 収益 - 費用
• 利益計画を立てるための基本的な関係はCVP関係

利益目標が立つとその達成のために必要な販売量・価格・セールズミックス等を検討しなければならない。

その際に使われるのがCVP (cost-volume-profit)分析。

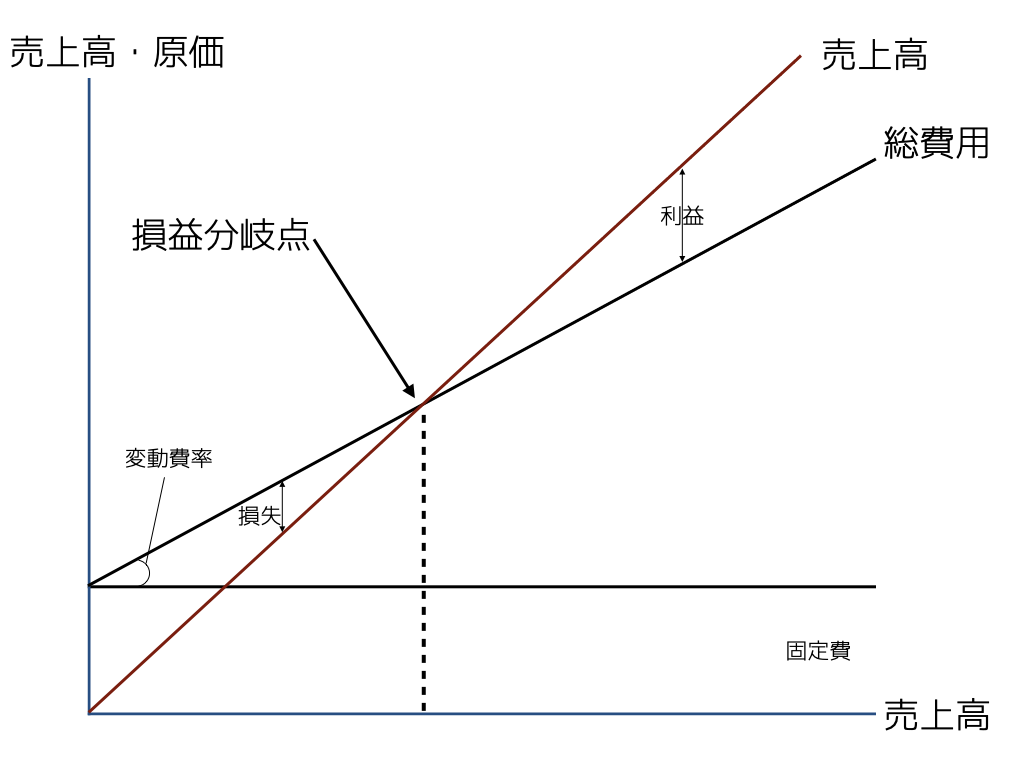
4.2 損益分岐点（Breakeven point）

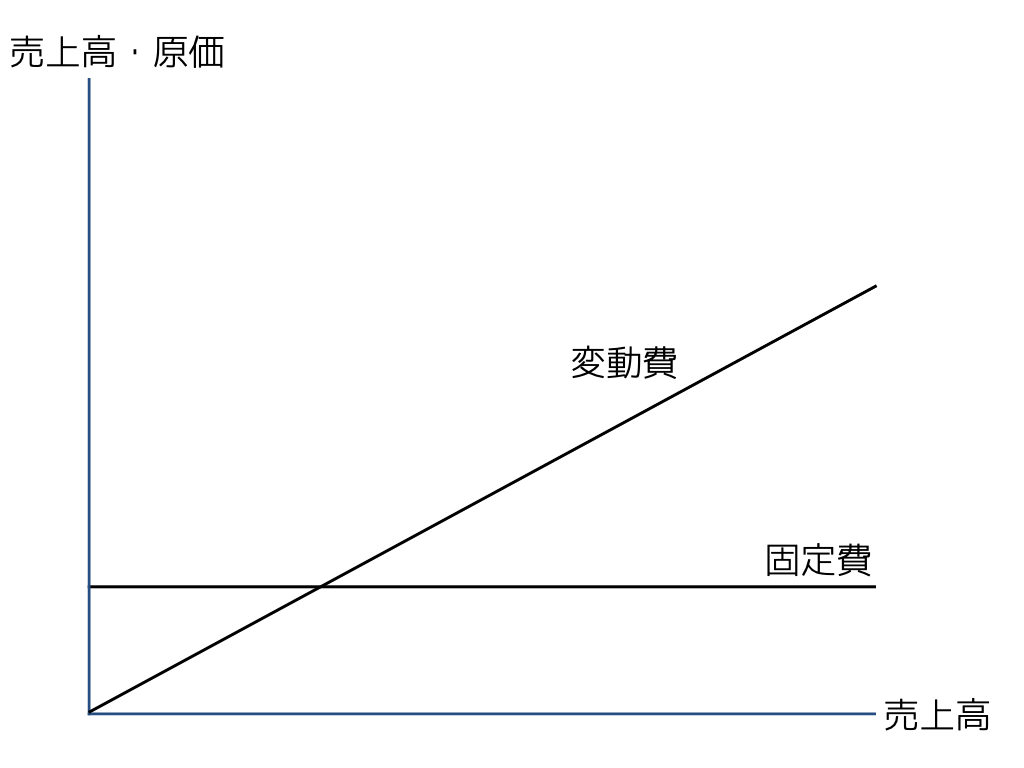
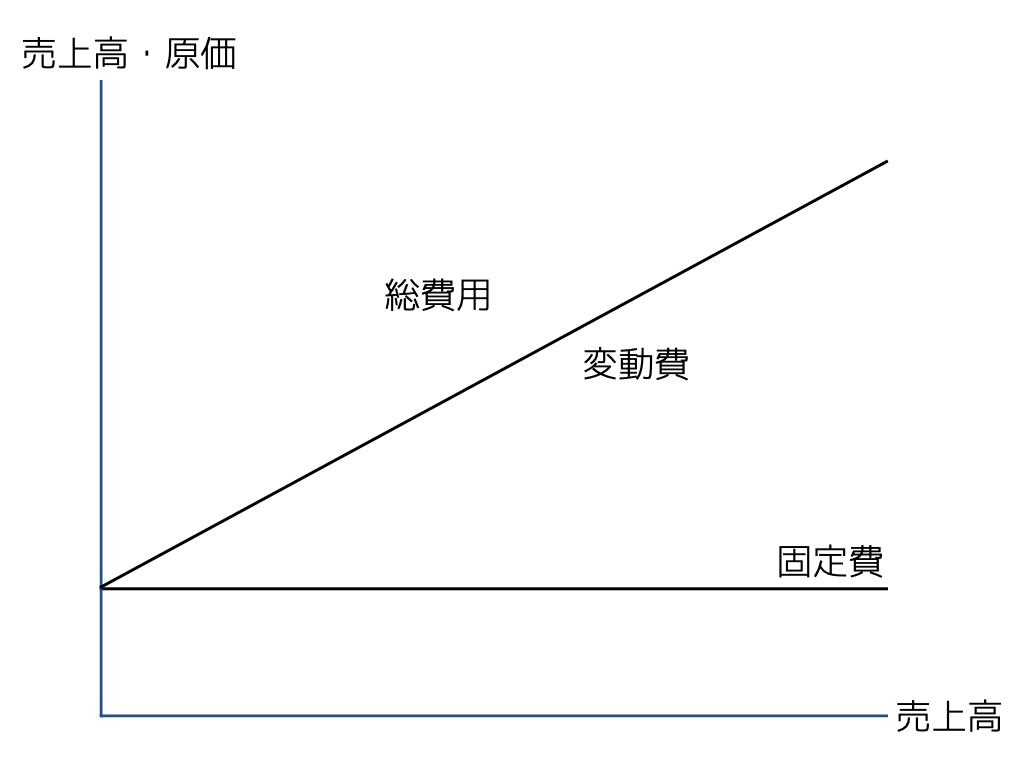
• 縦に金額（売上高や原価）・横に活動量（売上高や生産量）をとったグラフを使って利益の推移を図示する。
• 原価は固定費と変動費に分解すると，売上高に比例して大きくなるのは変動費部分。この売上高に対する変動費の金額（傾き）を変動費率という

横軸を売上高とすると…

売上高：\(Sales = Sales\)

原価：\(Cost=a + bSales\)

\(a\)は固定費，\(b\)は変動費率

損益分岐点は売上高と原価が一致する\(Cost = Sales\)

\[ \begin{split} Sales &= a +bSales \\ &= \frac{a}{1-b} \\ &= \frac{\text{固定費}}{1 -\text{変動費率}} =\frac{\text{固定費}}{1 - \frac{\text{変動費}}{\text{売上高}}} \\ & =\frac{\text{固定費}}{\text{限界利益率}} \end{split} \]

横軸を販売数量\(x\)，単価を\(p\)とすると…

売上高：\(Sales = px\)

原価：\(Cost=a + bx\)

\(a\)は固定費，\(b\)は変動費率

損益分岐点は売上高と原価が一致する，つまり\(Cost = Sales\)。その時の販売数量は

\[ \begin{split} px&= a +bx \\ x &= \frac{a}{p-b} \\ &= \frac{\text{固定費}}{\text{単価} -\text{変動費率}} \\ &=\frac{\text{固定費}}{\text{単価} - \frac{\text{変動費}}{\text{売上高}}} \end{split} \]

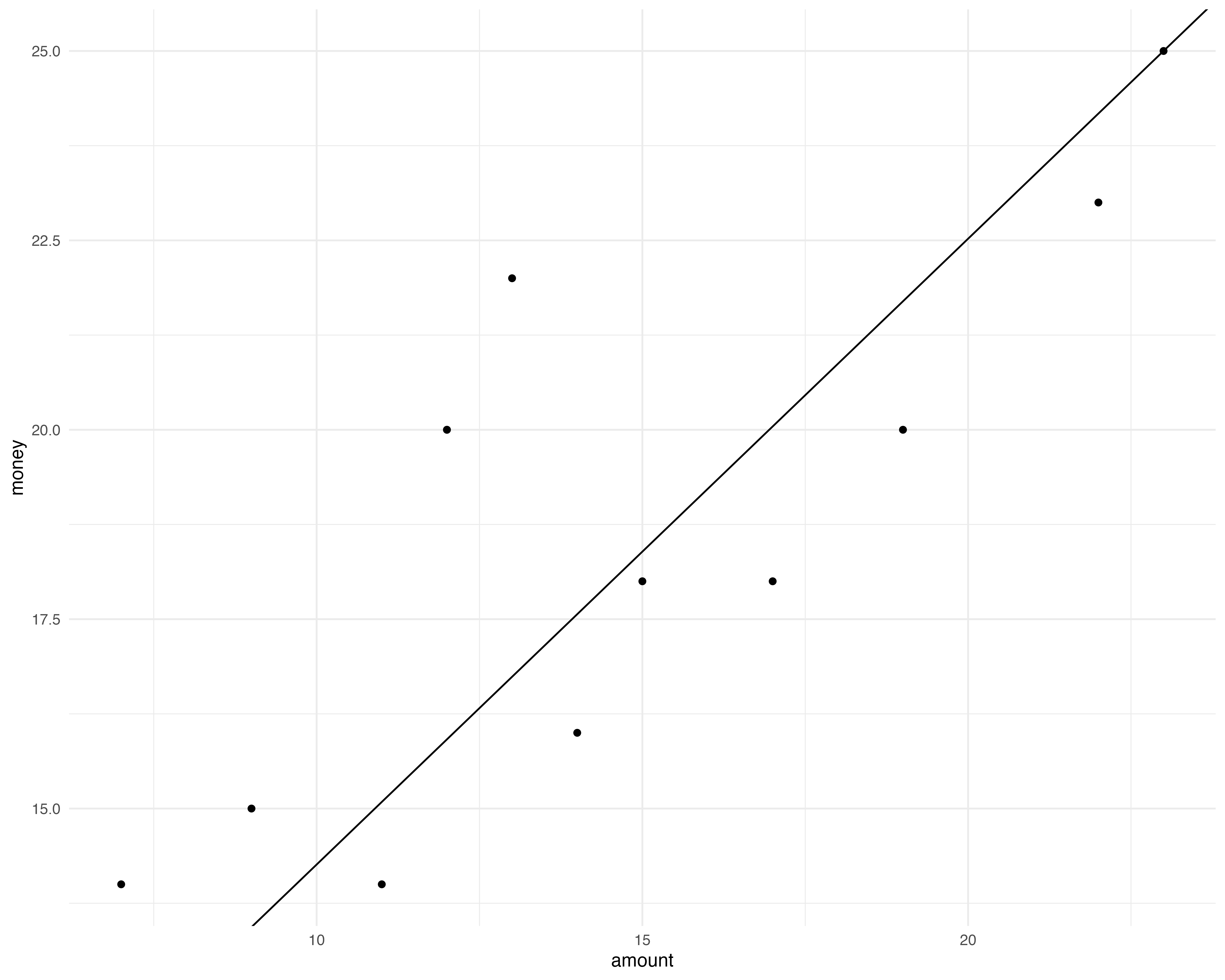
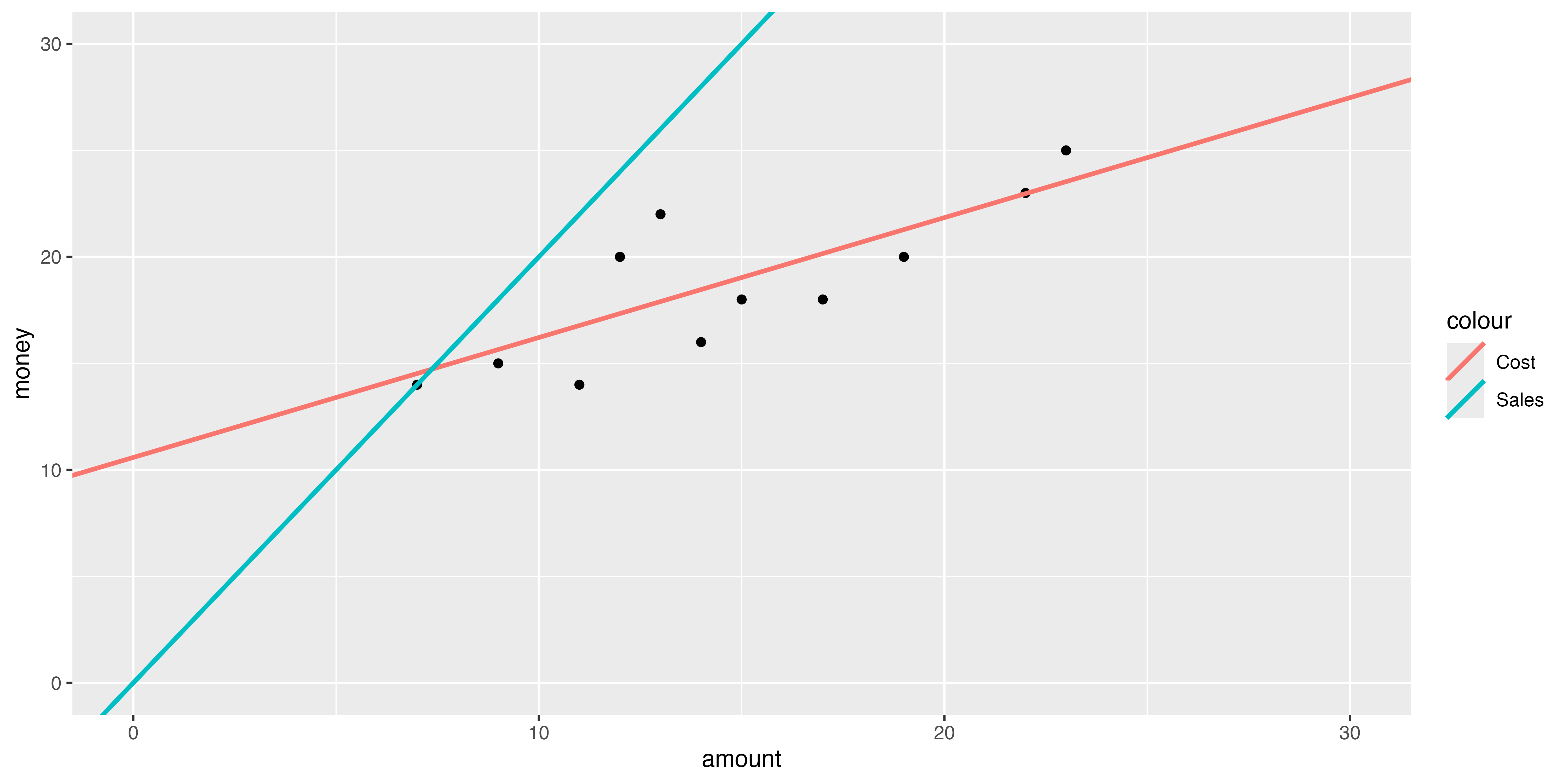
先ほどの例で，販売単価が2だとすると，売上高線は\(y = 2x\)になる。これと最小二乗法で求めたコスト線を表に書くと…

data |>  
  ggplot(aes(x = amount, y = money)) +
  geom_point() +
  geom_abline(linewidth = 1, 
              aes(slope = 0.563, 
                  intercept = 10.584, 
                  color = "Cost")) +
  geom_abline(linewidth = 1, 
              aes(slope = 2, 
                  intercept = 0, 
                  color = "Sales")) +
  scale_color_manual(values = c(Cost = '#f8766D', 
                                Sales = '#00BFC4')) +
  scale_x_continuous(limits=c(0,30)) +
  scale_y_continuous(limits=c(0,30))

損益分岐点は2つの線の交点なので，以下のような連立方程式の解（ベクトルとして解くために順番変えてます）

\[ \begin{cases} 0.563x - y = -10 \\ 2x - y = 0 \end{cases} \]

Rで連立方程式を解いてみたい→解いてみた

a <- matrix(c(0.563, -1, 2, -1), nrow = 2, byrow = TRUE)
b <- matrix(c(-10, 0), nrow = 2, byrow = TRUE)
a

      [,1] [,2]
[1,] 0.563   -1
[2,] 2.000   -1

b

     [,1]
[1,]  -10
[2,]    0

ans <- solve(a,b)

amount が 6.959 ，moneyが 13.918

4.3 CVP分析の活用

4.3.1 利益計画とその策定

• 経営戦略を長期的な数値目標に置き換えたのが中長期経営計画
• 中長期経営計画を受けて，必要な活動を短期の目標（短期利益目標）の観点から総合調整した計画
• より具体的で細分化された予算を編成するための方針となる
• 利益計画の策定に際しては，コストを直接費と間接費にわけた上で，売上高との関係を検討するCVP分析が使われる。
  • CVP分析を行うことによって，例えば目標利益を上げるためには，どれぐらいの売上が必要そうか，どれぐらいの製造キャパシティを計画すれば良いか，などがわかる。

4.3.2 CVP分析を受けてどのような行動をとる？

利益を増やす方法は，

売上高を増やす

---

• 価格を上げる
• 販売量を上げる

コストを減らす

---

• 変動費率を下げる
• 固定費を減らす

のいずれか。ただし，それぞれの意思決定が他の要因に与える影響を予測する必要がある。これをしないと，結果として利益が下がる場合がある。

• 価格を上げることで，販売量が減るかもしれない
  • 販売量が減ると，製品1単位あたりの固定費負担が増えるかもしれない
• 販売量を上げるためには，製造原価以外の費用（広告宣伝費など）が増えるかもしれない

また，固定費は，文字通り固定的に構造化されている費用が多い（人件費，店舗賃貸料など）。これを下げる場合，構造をつくりかえること，すなわちリストラクチャリング（リストラ）が必要となる場合も。その場合一時的に大きいコストがかかる可能性がある。

• 固定費には，コミッテッド・キャパシティコスト（comitted capacity cost）とマネジド・キャパシティコスト（managed capacity cost）があるんだった（固定費のタイプ: Committed と Discretionary）

• 短期的な利益計画達成のためには，managedの方の広告費・研究開発費・修繕維持費などを調整することが可能であるが，例えば研究開発費の削減は，長期的な収益性に対して悪影響を与える可能性もある。

• またcomittedの方についても，長期的な視野に立ったコントロールが必要。

5 実習

5.1 課題

ある工場では、製品Aと製品Bの2つの製品を生産しています。この工場では、生産量に基づいて総原価が変動しますが、固定費も存在します。各製品の生産量と総原価に関するデータが12_cvp_kadai.csvのように与えられています。（Month: 月，Product: 製品の種類，Production: 生産量，Total_Cost: 総費用）

1. 上記のデータを使用して、製品Aと製品Bの総原価に対する固定費と変動費を分解する回帰分析を行いなさい。分析には製品ダミー変数を使用し、それぞれの製品ごとの原価を推定してください。
2. 回帰分析の結果から、各製品の固定費と変動費率をそれぞれ読み取ってください。
3. 回帰分析の結果を図示してください（製品ごとの総費用線を引いてみてください）。

ヒント1: 推定

• 製品ダミー変数を使用して、製品Aのデータを0、製品Bのデータを1とします。
• 回帰分析のモデルは次のようになります： \[TotalCost_i = \beta_0 + \beta_1 Production_i + \beta_2 ProD_i + \beta_3 Production \times ProD_i + \epsilon\]
  ここで、\(\beta_0\)は固定費、\(\beta_1\)は変動費率（共通）、\(\beta_2\)は製品BとAの固定費の差， \(\beta_3\)は製品BとAの変動費率の差を表します。 \(Production\)は生産量， \(ProD\) は，製品を識別するダミー変数（変数名は自由に設定いただいて構いません）です。ダミー変数で場合わけすると，以下のようになります。
  \[ \begin{cases} TotalCost_i = \beta_0 + \beta_1 Production_i + \epsilon & Product A\\ TotalCost_i = (\beta_0 + \beta_2) + (\beta_1 + \beta_3) Production_i + \epsilon & Product B \end{cases} \]

ヒント2: 図示

• 製品ごとに散布図の色を分けたかったら，aes()の中に（color = Product）を入れるといいです。

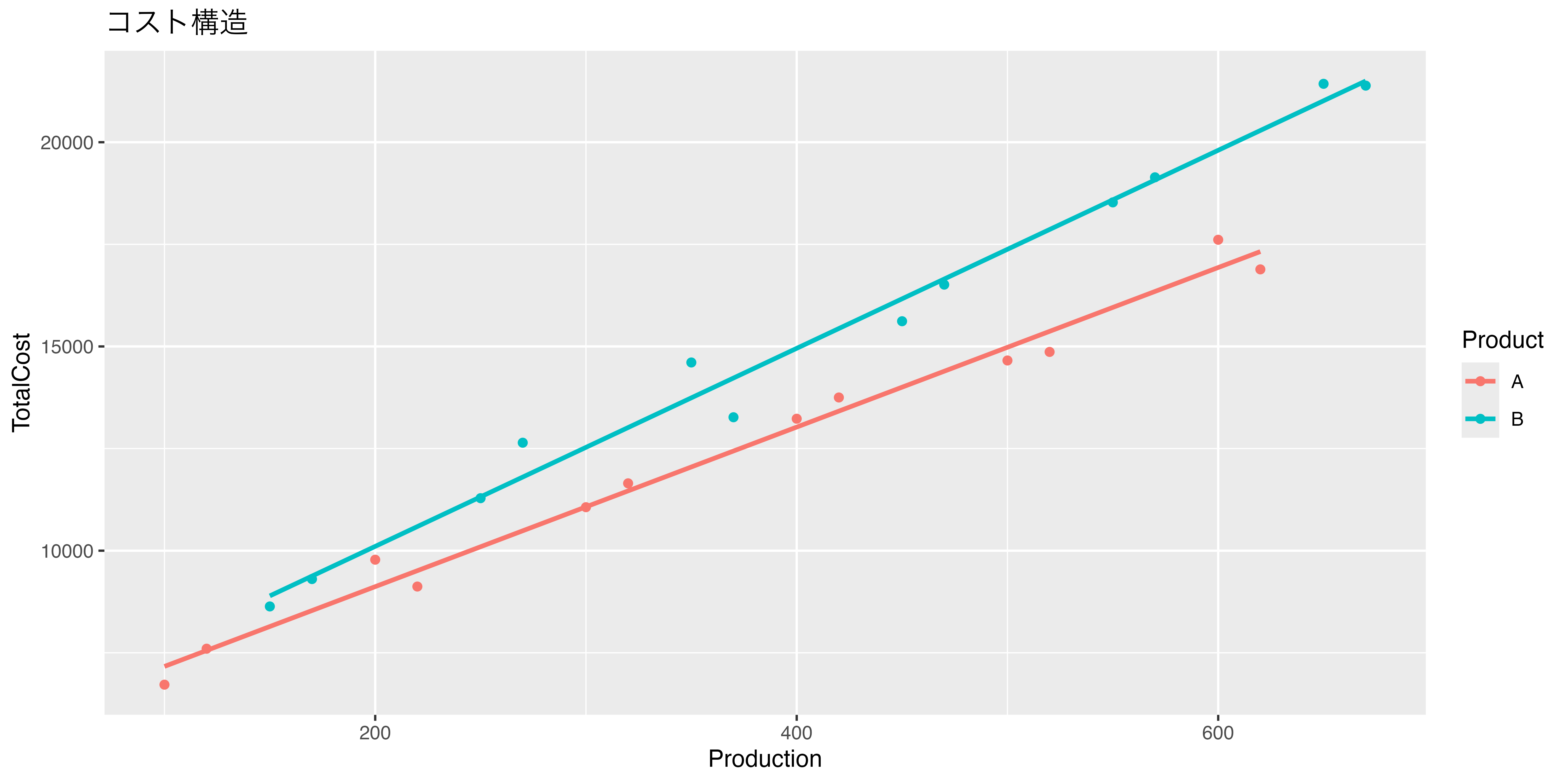
5.2 答え

data <- here("data", "11_cvp_kadai.csv") |> read_csv()
# 回帰分析の実施
model <- lm(Total_Cost ~ Production * Product, 
            data = data)
summary(model)

Call:
lm(formula = Total_Cost ~ Production * Product, data = data)

Residuals:
   Min     1Q Median     3Q    Max 
-960.1 -339.1  -47.9  236.8  865.6 

Coefficients:
                    Estimate Std. Error t value            Pr(>|t|)    
(Intercept)         5213.548    334.606   15.58 0.00000000000119145 ***
Production            19.531      0.839   23.27 0.00000000000000059 ***
ProductB              43.363    501.054    0.09             0.93189    
Production:ProductB    4.712      1.187    3.97             0.00076 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 498 on 20 degrees of freedom
Multiple R-squared:  0.988, Adjusted R-squared:  0.986 
F-statistic:  529 on 3 and 20 DF,  p-value: <0.0000000000000002

# 回帰直線の描画
ggplot(data, aes(x = Production, 
                 y = Total_Cost, 
                 color = Product)) +
  geom_point() +
  geom_smooth(method = "lm", 
              se = FALSE) +
  labs(title = "コスト構造",
       x = "Production",
       y = "TotalCost")

\[ TotalCost_i = \beta_0 + \beta_1 Production_i + \beta_2 ProD_i + \beta_3 Production \times Prod_i + \epsilon \]

なので，

\[ \begin{cases} TotalCost_i = \beta_0 + \beta_1 Production_i + \epsilon & Product A\\ TotalCost_i = (\beta_0 + \beta_2) + (\beta_1 + \beta_3) Production_i + \epsilon & Product B \end{cases} \]変動比率に差がある。19.531 がAの変動費率，24.243 がBの変動費率

製品Aの固定費は，切片の5213.548 、固定費の差は有意ではないし，ほとんど変わらないが，Bの固定費は5256.911程度

6 参考文献

Tracy, J. A., and T. C. Tracy. 2014. How to read a financial report : Wringing vital signs out of the numbers. 8th ed. Hoboken, NJ.: John Wiley & Sons.

福嶋誠宣., 新井康平., and 松尾貴巳. 2014. 自由裁量費のコスト・ビヘイビアがCVP分析に与える影響. 会計プログレス 2014 (15): 26–37.

谷武幸. 2022. エッセンシャル管理会計. 第4版 ed. 東京: 中央経済社.